XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> Multiaxial Fatigue Theory
Before attempting to read and understand this section, it is highly recommended that you be intimately familiar with basic fatigue theory as described in
Fatigue Theory (Ch. 15).
Most engineers, if they consider the possibility of fatigue failure at all, adopt the simple S-N approach developed during the last century. Modern software design tools such as MSC Fatigue incorporate fatigue concepts such as Miner’s rule (1920s), the strain-life approach (1950s), and linear elastic fracture mechanics (1960s). These ideas are well tried and tested and their limitations well understood. Universities and research departments of some companies in major industries, notably power generation, ground vehicle and aerospace, are engaged in active research into new areas. Theories in these areas are much less well-established and understood. Therefore, predictions based on these ideas should be treated with some caution. Included in this category are elastic-plastic fracture mechanics, fatigue life in the short crack regime, and multiaxial fatigue.
Multiaxial Stress-Strain State
Up until recently, uniaxial cyclic loading has been implicit in the discussion of both high- and low-cycle fatigue. However, many real design situations, including rotating shafts, connecting links, automotive and aircraft components and many others involve a multiaxial state of cyclic stress. This often means that, at any point, the directions of the principal stresses can vary during the loading cycle and are therefore a function of time. Furthermore, the magnitudes of the principal stresses themselves may no longer be proportional to each other. Both these effects complicate the analysis required for the prediction of fatigue behavior. To some extent, the situation can be clarified through an understanding of the differences in the stress-strain states that prevail under simple uniaxial loading and nonproportional multiaxial loading.
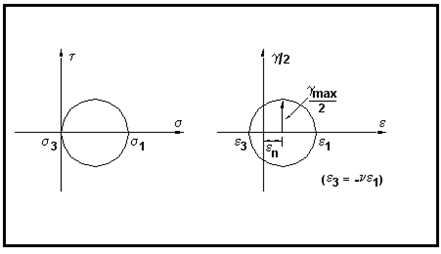
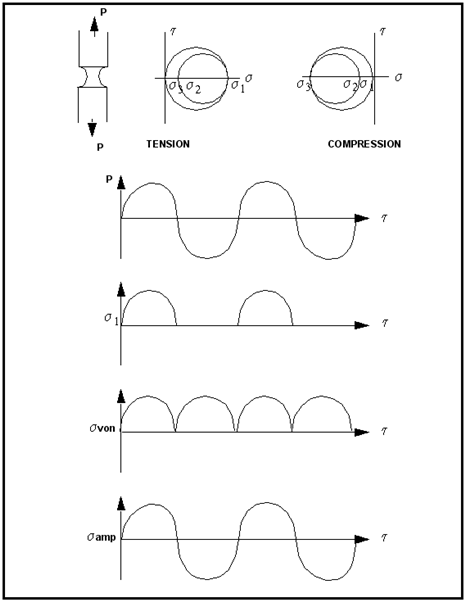
Figure 6‑33 The Stress-Strain State in Uniaxial Tension
Separate Tensile or Torsional Loading
A snapshot, in terms of the Mohr’s circle representation, of the stress-strain state prevailing under a static load in both tension or torsion loading is presented in
Figure 6‑33 and
Figure 6‑34. For uniaxial tension,
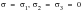
and
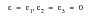
the Mohr’s circles for stress and strain appear as in
Figure 6‑35.
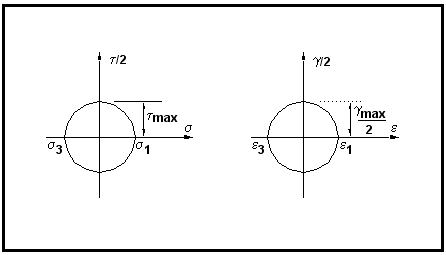
Figure 6‑34 The Stress-Strain State in Torsion
For pure shear as in the case of a torsion test,
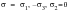
and
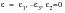
(the Mohr’s circles for stress and strain appear as in
Figure 6‑34). During cyclic loading, the diameter of the Mohr’s circle varies depending on the magnitude of the cyclic stress or strain.
Figure 6‑35 illustrates this effect for bar subjected to a constant amplitude uniaxial strain cycle.
Figure 6‑35 Mohr's Circles for a Uniaxial Strain Cycle
Combined Tensile and Torsional Loading
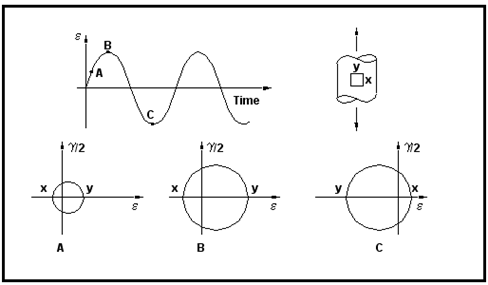
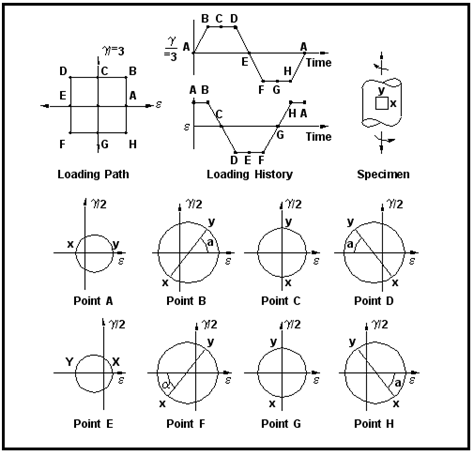
It often happens in practice that separately-induced load cases can result in
non-proportional loading environments.
Figure 6‑36 can be used to illustrate the point by detailing the variation of axial and torsional strain with respect to time during the course of a complete fatigue cycle. Note that the loading path is no longer a straight line between normal and shear strain but rather a rectangular function. Note also that the direction of the principal strain is no longer fixed (i.e., the line x-y subtends an angle α with the strain axis).
Figure 6‑36 Non-proportional Loading Sequences
Mechanisms of Fatigue Damage Accumulation
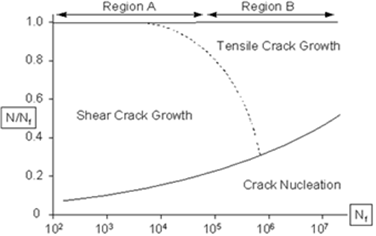
Fatigue damage can be understood to be a process in which cracks initiate and then propagate until final failure. Crack initiation has been demonstrated to be the result of reversed plastic flow (i.e., the forward and backward motions of dislocations along the slip planes of metallic crystals). Slip occurs along planes of maximum shear, and will first appear in those grains which are most favorably oriented with respect to the maximum applied shear stress. In 1961, Forsyth proposed a two stage model for early crack growth.
Stage I is a period of nucleation and crystallographically orientated growth following immediately after initiation and is confined to shear planes. In this phase, both the shear stresses and strains and the normal stresses and strains are the moduli which control the rate of crack extension.
Stage II growth is growth which occurs on planes which are orientated perpendicular to the maximum principal stress range. In this phase, the magnitude of the maximum principal stresses and strains dominate the crack growth process.
The proportion of life spent within each of these modes has been shown to depend on material type, ductile versus brittle, loading mode and amplitude. It is interesting to note that even in the case of non-proportional loading, Stage I fatigue cracks nucleate and grow on the plane of maximum shear strain range (which is subjected to the largest amplitude of normal strain).
Since initiation life refers to the time taken to develop an engineering crack, the initiation phase may include both stages of crack development. In practice, Stage I or Stage II may dominate lifetime. In uniaxial fatigue, this is not so much of a problem as the controlling parameters in both cases are directly related to the uniaxial stress or strain. In multiaxial fatigue this is no longer the case. Furthermore, the Stage I to Stage II transition is sensitive to the material and the precise nature of the loading. It follows that it is very difficult to apply general rules, and a model that produces good predictions for a given material and loading may no longer hold true when applied to a different situation. To add further confusion, there may be interaction between damage on different planes. That is to say, cracks growing on a particular plane may actually impede the progress of those growing on a different plane and lead to an increase in fatigue life.
Any theory of multiaxial fatigue must attempt, to a greater or lesser extent, to incorporate some of these physical observations if it is to have any chance of being successfully applied to real situations.
Theories of Multiaxial Fatigue
Traditionally, the approach to the design of components subjected to multiaxial loading is to make the following fundamental assertion:
Failure under a multiaxial loading is predicted to occur, according to the theory associated with a particular modulus, if and when the cyclically induced magnitude of that modulus, is sufficiently large that failure would occur in the uniaxial state for an identical magnitude of the same modulus.
The mechanical modulus referred to above, is a measurable quantity such as principal stress, principal shear stress or distortion energy. The range of the modulus may be defined by any two appropriate and independent values of it such as
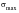
, and
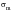
or
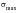
and
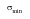
.
This philosophy has lead to what is usually referred to as equivalent stress-strain approach, where an equivalent stress or strain modulus is calculated under multiaxial loading and then applied to uniaxial data.
A problem with all of the methods is that they do not take into account the fact that fatigue is essentially a directional process, with damage (i.e., cracking) taking place on particular planes. In addition, there are problems in applying any of these methods to situations of non-proportional loading (i.e., where the number of load inputs is greater than one, and these loads have a non-constant ratio or phase relationship).
This has led to a much greater research emphasis being placed on understanding the underlying mechanisms of fatigue damage accumulation under multiaxial loading. Out of this work has arisen a somewhat different approach to fatigue life estimation based on predicting the extent of damage in specific directions and planes within the component. This methodology is usually referred to as the critical plane approach.
Equivalent Stress-Strain Approaches
These approaches are based on extensions to static yield theories. They assume that lifetimes for fatigue under multiaxial loading can be predicted by substituting combined stress or strain parameters in the uniaxial stress-life or strain-life equations (i.e., by calculating an equivalent uniaxial stress or strain for a given multiaxial loading). The main stress and strain parameters used are the maximum principal, the maximum shear (related to the Tresca criterion), and the von Mises or octahedral. The big advantage of this kind of approach is that it enables the large amount of uniaxial fatigue test data available in the literature or in data banks to be applied to multiaxial situations.
The von Mises method has gained widest acceptance, but all these methods have drawbacks. In the Tresca criterion, the median principal stress does not affect the equivalent stress or strain, and neither of the von Mises or Tresca criteria varies with the application of a hydrostatic stress, contrary to experimental evidence.
Before proceeding further with a more detailed account of the various equivalent stress-strain theories evolved to account for dynamic multiaxial stresses, it is worth examining the basis of the stress-strain combination procedures developed to account for static failure under multiaxial stresses.
Combined Stress Theories of Static Failure
Predicting failure and establishing a geometry that will avoid failure is relatively straightforward if a component is subjected to a static uniaxial stress. It is only necessary to refer to a uniaxial stress-strain curve for the material of interest and ensure that the service loading is less than some critical value. For example, if yielding is the failure mode to be avoided, then failure would be predicted to occur when the maximum principal stress exceeds the yield stress. However, if the component under consideration is subjected to a multiaxial loading, failure prediction is much more complicated. It is no longer possible, for example, to predict when yielding will occur through a consideration of the maximum principal stress alone because the other principal stresses will also have an influence.
A large number of multiaxial tests would be required in which all of the stress components would have to be varied over their entire range of values in all possible combinations in order to adequately describe the above situation. Such a testing program would be prohibitively expensive and perhaps not even possible for certain stress states. When faced with such complex situations engineers always attempt to develop a theory that relates behavior in the complex situation to behavior in a simple easily evaluated test through some characteristic modulus. Specifically, when it is required to predict the failure of a component subjected to multiaxial loading, it is usually to utilize a theory that relates failure in the multiaxial state to failure in a tension test through a well chosen modulus such as stress, strain or energy. To be useful such moduli must be calculable in the multiaxial state of stress and readily measurable in the uniaxial evaluation test. Therefore, a combined stress failure theory must contain three essential ingredients:
1. It must provide a model that relates external loading to the stresses and strains at the critical point in the multiaxial state of stress.
2. It must be based on physical properties of the material that are measurable.
3. It must relate the calculable mechanical modulus in the multiaxial stress state to a measurable criterion of failure based on the critical physical properties determined in a simple tension test.
A number of combined stress failure theories that contain these ingredients have been postulated. Numbered amongst these are the following: the maximum principal stress theory, the maximum principal strain theory, the maximum shear stress theory, the total strain energy theory, the distortion energy theory, Mohr’s failure theory. Two of these theories, the distortion energy and the maximum shear stress, will be developed in more detail with failure being considered to be yielding.
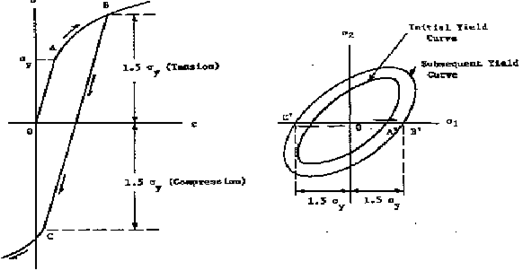
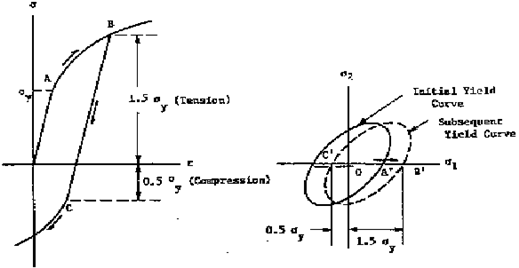
Yielding Criteria for Ductile Metals
As mentioned in the example above, yielding under uniaxial loading begins at the yield stress,
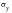
. Under combined loading, it is expected that yielding will occur at some particular combination of principal stresses. At present, there is no theoretical way of deducing the relationship between the stress components to correlate yielding for a multiaxial stress state with yielding in the uniaxial tension test. Therefore, yield criteria are empirical relationships. However, a yield criterion must be consistent with a number of experimental observations, the main one being the fact that pure hydrostatic pressure does not cause yielding in a continuous solid. This for example, rules out the use of the maximum principal theory since it would predict yielding failure when the magnitude of the maximum principal stress

becomes equal to the yield stress σy.
Since the hydrostatic stress component of a complex stress state does not influence the stress at which a material yields, the yield criterion must be based on the stress deviator. Moreover, for an isotropic material the yield criterion must be independent of the choice of axes (i.e., it must be an invariant function). These considerations lead to the conclusion that the yield criterion must be some function of the invariants of the stress deviator. At present, there are two generally accepted criteria for predicting the onset of yielding in ductile metals.
von Mises' or Distortion-Energy Theory
In 1913, von Mises proposed that yielding will occur when the second invariant of the stress deviator, J2 exceeds a critical value, i.e.,
(6‑24)
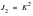
where
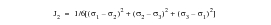
The constant k can be evaluated and related to yielding in a tension test by realizing that

, and
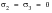
, and by substituting this for J2,
(6‑25)
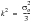
and so the von Mises’ prediction of yield in terms of the principal stresses becomes,
(6‑26)
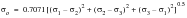
and yielding will occur when
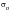
exceeds the monotonic yield stress. In terms of the (x,y,z) component stress, it may be written as:
(6‑27)
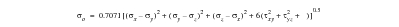
By considering the state of stress for pure shear as in a torsion test, it is possible to identify the constant k. In torsion,
and
at yield
(6‑28)
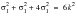
This means that k represents the yield stress in pure shear, torsion. Therefore, the von Mises’ criterion predicts that the yield stress in torsion will be less than that for uniaxial tension according to:
(6‑29)
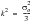
In 1924, Hencky derived the von Mises’ yield criterion through a consideration of distortion energy and so it is sometimes also referred to as the distortion energy criterion.
Maximum Shear Stress or Tresca Theory
The Tresca yield criterion suggests that yielding will occur when the maximum shear stress under multiaxial loading reaches the value of the shear stress under uniaxial tension test. Since according to convention
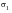
is the algebraically greatest principal stress and
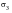
the smallest, the maximum shear stress,
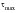
is given by:
(6‑30)
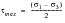
For uniaxial tension,

, and
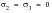
, and the shearing yield stress
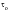
is equal to
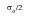
and so
(6‑31)
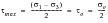
and
(6‑32)
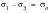
For the state of pure shear
, 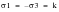
and

, the maximum shear stress criterion would predict yielding will occur when
(6‑33)
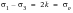
and so the maximum shear stress criterion predicts that yield in torsion will be less than in uniaxial tension according to:
(6‑34)
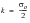
It is worth noting that the Tresca criterion appears much simpler than that proposed by von Mises and for this reason it is often used in engineering design. However, the maximum shear criterion does not take into account the intermediate principal stress. Furthermore, it suffers from the major difficulty that it is necessary to know in advance which are the maximum and minimum principal stresses.
Combined Stress States
The conditions for yielding or fatigue damage accumulation for that matter under stress states other than uniaxial or torsion loading can be studied experimentally with thin walled tubes. Axial stress can be combined with torsional loading to produce various combinations of shear stress to normal stress intermediate between the values obtained separately in tension or torsion. In addition, a hydrostatic pressure can also be introduced within the tube to induce circumferential hoop stresses.
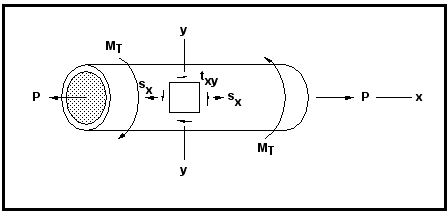
Figure 6‑37 illustrates such a thin-walled tube.
Figure 6‑37 The State of Stress in a Thin-Walled Tubular Specimen
For the thin-walled specimen shown above, the principal stresses can be calculated from:
(6‑35)
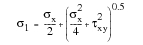
(6‑36)

(6‑37)
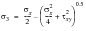
Under these conditions, the von Mises’ criterion would predict yielding when:
(6‑38)
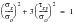
and the Tresca criterion would predict yielding when:
(6‑39)
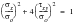
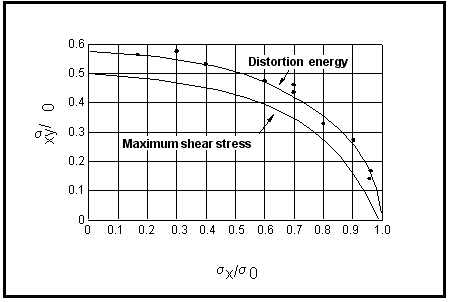
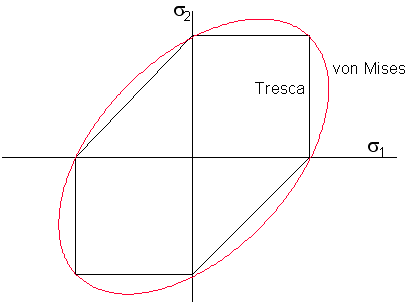
Both equations define an ellipse and
Figure 6‑38 shows that experimental results agree best with the von Mises’ approach.
Figure 6‑38 Comparison Between the Tresca and von Mises' Theories
Critical Plane Approaches
As the name suggests, critical plane approaches recognize that fatigue damage (cracking) is essentially directional and so consider the accumulation of damage on particular planes. This is in contrast to the equivalent stress-strain approaches which may be summing damage that is occurring on different planes. A range of methods for calculating damage on a particular plane is used. These methods include:
1. Simply resolving the normal strain on the plane and applying what is essentially a uniaxial analysis.
2. As above, but allowing for the multiaxial nature of the stresses through a consideration of the out-of-plane hardening.
3. Variations on the Brown-Miller approach, which consider the shear strain amplitude in the plane and the normal stress or strain.
Typically, damage is calculated for all possible planes (at, say 10 degree intervals) and the worst or critical plane selected.
Fatigue cracks normally initiate on planes of maximum shear and grow initially in mode II (shear mode), changing to mode I (opening mode) where the maximum principal may be important. In brittle materials or where initiation occurs at inclusions, growth may be in mode I from the outset. Since initiation life refers to the time taken to develop an engineering crack, this so-called initiation phase may include both stages of crack development. In practice, Stage I or Stage II may dominate lifetime. In uniaxial fatigue, this is not so much of a problem, as the controlling parameters in both cases are directly related to the uniaxial stress or strain. In multiaxial fatigue, this is no longer the case. Furthermore, the Stage I to Stage II transition is sensitive to the material and the precise nature of the loading. It follows that it is very difficult to apply general rules, and a model that produces good predictions for a given material and loading may no longer hold true when applied to a different situation. To add further confusion, there may be interaction between damage on different planes; cracks growing on a particular plane may actually impede the progress of those growing on a different plane and lead to an increase in fatigue life.
The Miller-Brown Parameter
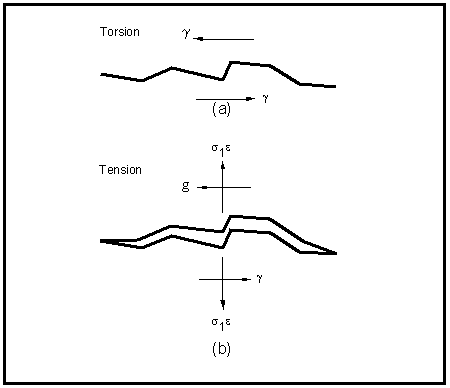
In addition to the importance of the plane of maximum shear, the stress and strain normal to this plane has also been recognized to strongly influence the development of fatigue cracks. This point can be illustrated by referring to
Figure 6‑39.
Figure 6‑39 (a) Shear Strain (b) Shear Strain and Normal Stress-Strain
It is clear from
Figure 6‑39 (a) that the shear strain,
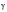
, acting on the plane of maximum shear will extend the fatigue crack and, amongst other things, progress will be opposed by the friction between the crack faces. If a tensile stress or strain is applied normal to the plane, then the surfaces are separated and the frictional opposition reduced and more damage can be accumulated at the crack tips. Under these circumstances, fatigue damage can be expected to accumulate more rapidly and life to be reduced.
These ideas, whilst recognized by Mohr and others, were first formulated by Miller and Brown who presented a two parameter formulation as:
(6‑40)
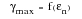
γmax | | is the maximum shear strain |
εn | | is the strain normal to the above shear |
They proposed that the maximum shear strain is the primary force in crack initiation and that the strain normal to the plane of maximum shear is a modifying factor. The above equation has been modified by Kandil and later by Fash to develop it into a damage law based on uniaxial cyclic properties:
(6‑41)
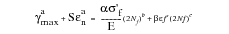
where
:
γmax | | is the maximum shear strain amplitude |
εn | | is the strain amplitude normal to the plane of maximum shear |
The constants
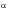
and
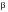
can be calculated from:
(6‑42)
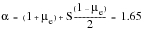
(6‑43)
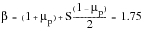
where
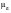
and
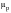
are respectively, the elastic and plastic Poisson’s ratios and the constant S is taken to be unity. The damage law now becomes:
(6‑44)
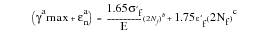
Note that this is similar to the Tresca formulation but with the normal strain component added, and as it stands, takes no account of the fact that the plane of maximum shear, like the principal stresses and strains, could rotate.
Non-Proportional Loadings and the Bannantine-Socie Approach
When loadings are multiaxial and non-proportional, it is possible that the directions of the principal strains (and hence also the shear strains) and their ratios may change with time. Under these circumstances, the Miller-Brown parameter is not effective, because it has no way of dealing with the shear plane rotation.
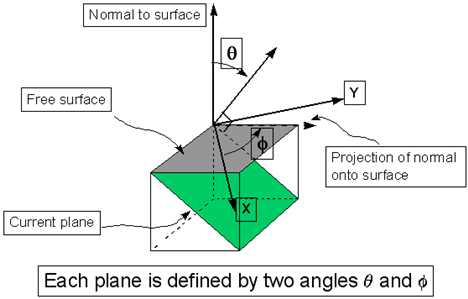
The Socie-Bannantine method has a different approach. Instead of defining the critical plane as the maximum shear plane, and calculating damage on that plane, it defines a critical plane damage parameter and searches for the plane on which the damage is a maximum. This plane is said to be the critical plane. Plane orientations can be described by means of two angles as shown in the following diagram.
Figure 6‑40 Plane Orientations Defined by θ and φ
In order to understand this better, it is necessary to review the behavior of short cracks. It has been noted earlier that there are two stages to crack growth, Stage I normally being shear cracking and Stage II opening mode. This is illustrated in
Figure 6‑41.
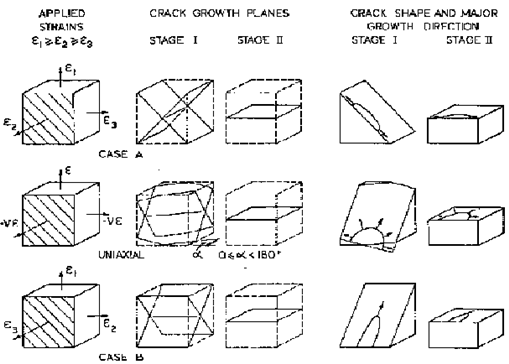
Figure 6‑41 Applied Strains and Crack Growth Planes
This figure illustrates how Stage II cracking is typically normal to the maximum principal stress or strain, and how the orientation of the maximum shear planes on which the Stage I cracks grow depends on the state of stress as described by the biaxiality ratio which is the ration of the smaller to the larger in-plane principal stresses (this discussion is restricted to free surfaces). However the relative importance of shear cracking and opening mode cracking is a function of the stress state, the loading level, mean stress, and the material. A basic premise of the Socie-Bannantine approach is that the life prediction method needs to reflect the damage mechanism as seen from the crack morphology. Based on this idea, they developed a number of damage “maps” for different materials which illustrate the dominant cracking mechanism under different loading conditions.
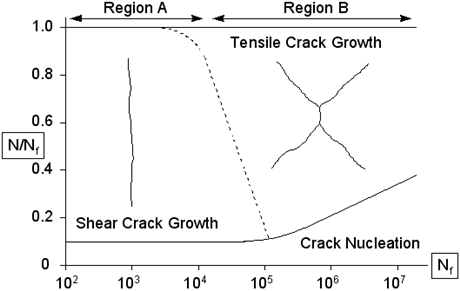
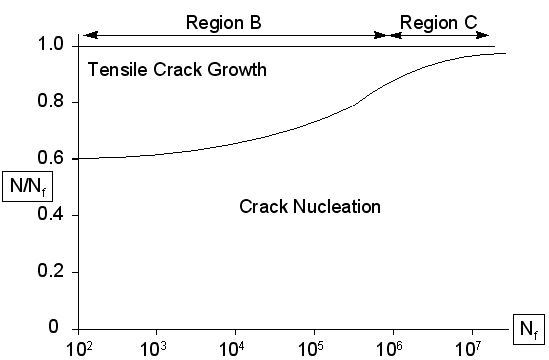
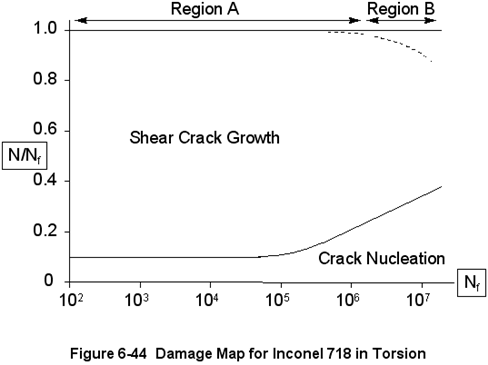
The following figures are damage maps (schematic) for two materials under two different stress states.
Figure 6‑42 Damage Map for 304 Stainless Steel in Torsion
Figure 6‑43 Damage Map for 304 Stainless Steel in Tension-Compression
Figure 6‑44 Damage Map for Inconel 718 in Torsion
Figure 6‑45 Damage Map for Inconel 718 in Tension-Compression
The Socie-Bannantine method has two damage models, one for situations where tensile cracking dominates and one for shear cracking. The equations are:
For the tensile model:
(6‑45)
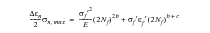
being very similar to the Smith-Watson-Topper approach, and for the shear model:
(6‑46)
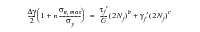
The shear model requires some torsional strain-life parameters. If these are not available, the above equation can be rewritten using uniaxial parameters. This formulation is devised to give the correct result under uniaxial conditions. It is this formulation that is used in MSC Fatigue:
(6‑47)
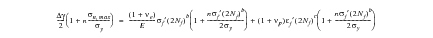
In theory these models should be used to search for the plane with the greatest fatigue damage. In practice, it is adequate for the tensile model to make calculations only on planes inclined at 90 degrees to the free surface, i.e.
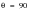
degrees, calculating at 10 degree intervals of

, making 18 planes in all. For the tensile model, it is necessary to search both Case A
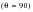
and Case B
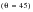
planes making 36 planes in all. The loss of accuracy is not significant.
The Wang-Brown Cycle Counting and Damage Approach.
The Socie-Bannantine approach is a good one, but has some shortcomings.
1. The shear model often predicts the greatest damage on planes which are a few degrees away from the maximum shear plane, contrary to the physical evidence. This is a minor philosophical objection.
2. The rainflow counting method it uses is essentially a uniaxial one, and as such, when the loading is non-proportional, it can identify a different set of turning points on every plane. This is not really in keeping with the philosophy of the rainflow method. A true multiaxial rainflow counting method should correspond to the hysteresis hardening process, i.e. it should identify reversals as elastic unloading, reloading and strain hardening in a multiaxial sense.
3. It tends to make somewhat non-conservative predictions for non-proportional loadings, which are more damaging.
Wang and Brown (Ref. 62)proposed a multiaxial cycle counting method on the basis of strain hardening behavior under non-proportional variable amplitude loading. Relative stresses and strains were introduced so that a pair of turning points define the start and end points of a reversal, where the equivalent relative strain rises monotonically to a peak value. Since plastic deformation generates the driving force for small fatigue cracks, hysteresis hardening provides a physical parameter for cycle counting, analogous to rainflow counting in the uniaxial case.
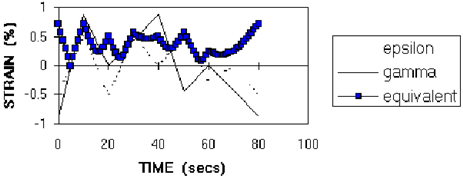
Each reversal commences with elastic unloading, which is followed by reloading and plastic strain hardening up to the next turning point. The most significant turning point occurs at the highest value of equivalent strain. This is illustrated at time 0 in
Figure 6‑46, which shows a repeating block of a combined tension/torsion non-proportional load history. The equivalent strain is defined as the von Mises strain.
Figure 6‑46 Variable Amplitude Non-proportional Strain History, Showing Applied Tensile (epsilon) and Torsional (gamma) Strains with the Absolute Equivalent Strain
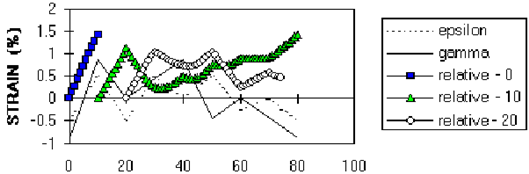
The cycle counting method is illustrated by the following example. Starting from the most significant turning point, a graph is drawn for the loading block of relative equivalent strain, where relative strain represents the change of strain since time A.
Figure 6‑47 shows the relative equivalent strain, with respect to times 0, 10 and 20 seconds. Using the relative strain, a reversal can be defined starting from 0, up to the maximum value 10 seconds. To obtain the second reversal, the relative strain is replotted starting from the next turning point where unloading commences (at 10 seconds), and the portions of the strain hardening curve for the reversal are selected by a traditional rainflow procedure (Ref. 56). The region of unloading and reloading within that reversal is counted in the next step.
Figure 6‑47 The Variable Amplitude History, Showing Relative Equivalent Strains Plotted with Respect to Times 0, 10 and 20 Seconds Respectively
Using the next turning point, relative strain is replotted with respect to 20 seconds for the subsequent continuous fragment of strain history, yielding the third reversal in
Figure 6‑47. This procedure is repeated for each turning point in chronological order, until every fragment of strain history has been counted.
Fatigue Damage Calculation
The counting method described above is independent of fatigue damage parameters, being based on hysteresis deformation behavior. Being unrelated to material properties, it can be integrated with any multiaxial fatigue damage model. If the counted reversals are non-proportional, a fatigue damage parameter that accounts for non-proportional straining effects is required. The path-independent damage parameter proposed by Wang and Brown (Ref. 63) has been shown to provide good correlation for several materials under proportional and non-proportional loading,
(6‑48)
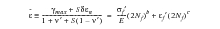
where
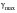
is the maximum shear strain amplitude on a critical plane (proportional or non-proportional),
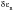
is the normal strain excursion between the two turning points of the maximum shear strain (that is the range of normal strain experienced on the maximum shear plane over the interval from start to end of the reversal), and

is the mean stress normal to the maximum shear plane. The term S is a material constant (the Brown-Miller parameter) determined from a multiaxial test (typically between 1 and 2 for Case A and around 0 for Case B) and
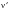
is the effective Poisson's ratio. The right hand side of the equation is the same as the uniaxial strain life equation, with a Morrow mean stress correction. Mean stress is measured as the average of the maximum and minimum stress values over the reversal. The total damage induced by a loading history is calculated using Miner's rule.
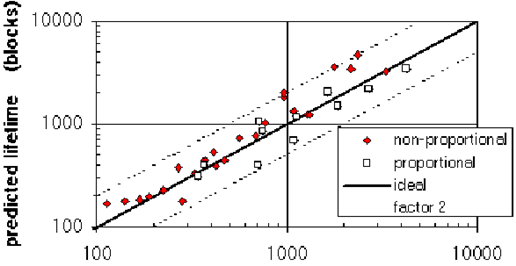
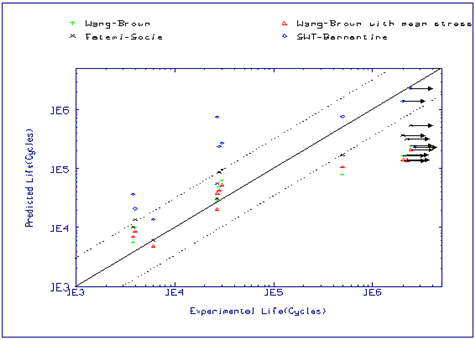
Figure 6‑48 is a plot of predicted life against experimental life for a variety of proportional and non-proportional tests on laboratory specimens, from (Ref. 48).
Figure 6‑48 Comparison of Experimental and Predicted Results for
the Wang-Brown Method
Figure 6‑49 below, illustrates a comparison of experimental and predicted results for four non-proportional tension-torsion loading paths, using the Wang-Brown method, with and without the mean stress term included, the Fatemi-Socie method (shear model) and the Bannantine (tensile) model. It is clear from this picture that for most of the results, the Wang-Brown methods give the best (and also the most conservative) results. The Fatemi-Socie model is next best and the Bannantine tensile model is very non-conservative, except for the longer lasting specimens, where the cracking behavior is more likely to be dominated by opening mode.
Figure 6‑49 Predicted vs. Measured Lives for Various Multiaxial Methods
Multiaxial Low Cycle Fatigue Analysis
The Concept of Similitude
Analytical fatigue life estimation procedures make it possible to replace some specific fatigue testing of components and structures by analysis based on measured or predicted loadings and cyclic tests on laboratory specimens. This process depends on the assumption that the damage (fractional damage or crack extension) to the component or structure is the same as the damage to the test specimens when subjected to the same loading and environment. This assumption of similitude can be described in more detail for each of the main fatigue life estimation procedures as follows:
1. In the strain-life or crack initiation method, the damage to a particular location in a component is assumed to be the same as the damage to a smooth fatigue specimen subject to the same strains. This means that the measured or predicted strains in a component can be related to the strain-life behavior of specimens in laboratory tests to predict lifetimes. The test specimens are normally smooth and cylindrical.
2. In the material S-N method, the damage to a particular location is the same as that at the critical location of a laboratory specimen subject to the same local stresses.
3. In the component S-N method, the damage to a component is assumed to be the same as that to a test component subject to the same nominal stresses. The geometry is assumed to be the same as the test pieces which will therefore have similar stress states.
4. In the crack propagation method, the crack growth rate in a component or structure is assumed to be the same as that in a specimen (usually a compact tension specimen) which is subject to the same stress intensity factors.
Taking the case of the local strain approach, polished cylindrical specimens are normally tested in strain controlled, fully reversed, constant amplitude, axial loading (push-pull). Real components are usually not polished and experience variable amplitude loading in environments other than laboratory air. There are well established ways of correcting for these differences, using rainflow cycle counting and surface finish and environmental corrections. However, there is another problem which is that the stress state of the specimens is uniaxial (i.e., there is only one non-zero principal stress and that is always aligned with the specimen axis), this will not in general be true of real components and structures, leading to a breakdown in similitude. If we are to carry out local strain fatigue analyses on components and structures subject to complex loadings we need means of:
1. assessing the stress states prevalent in the component or structure being analyzed, and
2. relating the damage caused by the stress and strain variations in the component or structure to that in the simple uniaxial test specimens.
Stress State Characterization
Any stress state can be completely described by the principal stresses (i.e., by their size and orientation). Now, the local strain approach models crack initiation. Cracks in smooth fatigue specimens normally initiate at free surfaces, and if they initiate elsewhere in the component being analyzed (e.g., from a defect within a weld), there is a serious problem with similitude. Now the stress states at free surfaces are relatively simple because the boundary conditions at the surface dictate that there can be no direct stresses on the plane of the surface or shear stresses normal to it. It follows that one of the principal axes of stress must be normal to the surface and the other two principal stresses must lie in the plane of the surface. The same applies to principal strains, except that the direct strain normal to the surface may be non-zero. Analysis and assessment can be greatly simplified because of these conditions, particularly if the FE stress and strain results are presented in an appropriate way. The state of plane stress existing at free surfaces means that any study of surface stress states can be reduced to a 2D problem if the results are presented in a suitable coordinate system, i.e. one whose x- and y-axes lie in the plane of the surface. In such coordinate systems, the z-normal stress and the x‑z and y‑z shear stresses and strains should all be zero. The deviation of these results from zero is a good indicator of the quality of the local stress information provided by the FE analysis. MSC Fatigue includes a utility which can be used to transform the surface stress and strain results to local coordinate systems where the z axes represents a surface normal. The surface stress state can now be investigated by looking at the x, y, and x‑y stresses only. It follows that the surface stress state can be completely described by the two in‑plane principal stresses and the orientation of one of them, the other being at right angles to the first.
For clarity, the conventional definition of the principal stresses, in which
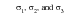
are ordered with
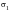
being most positive, is replaced (unless otherwise stated) by the following convention:
1. The principal stress normal to the surface is designated
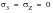
.
2. The other two principal stresses,
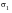
and
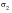
, are ordered in magnitude, so
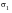
is now the absolute maximum principal stress, and
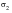
is the other in‑plane principal stress.
3. Similarly

and
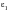
and
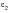
are ordered in magnitude.
The stress state at any surface point and instant can now be completely described by the value of the absolute maximum principal stress
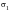
, the biaxiality ratio
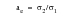
and the angle
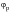
that
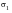
makes with the local x‑axis. At the surface of laboratory test specimens the stress state is uniaxial (i.e.,
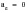
and
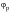
is constant). The stress state variations in real components or structures can deviate from uniaxial conditions in two respects:
1. The ratio of the principal stresses
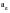
can be nonzero.
2. The orientation of the principal stresses
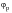
can vary with time.
MSC Fatigue is able to track these quantities throughout the time history and present the user with some summary statistics. These enable the most appropriate analysis to be carried out, and highlight cases where there may be problems with the validity of the analysis. The meaning of the statistics can be explained with the help of an example based on a motor vehicle chassis component subject to multiple multiaxial load histories derived from a track test. The absolute maximum principal stress
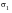
, the biaxiality ratio
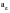
(which can vary between –1 and +1) and the angle
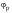
(which can vary between 0 and 180 degrees) were tracked and recorded for each element in the form of scatter plots of
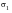
against
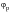
and
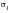
against
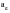
.
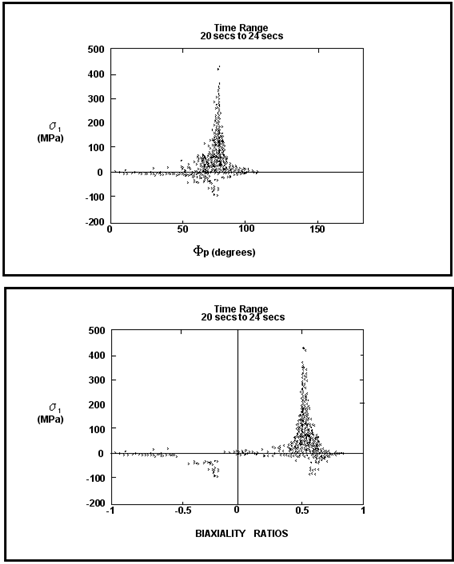
Figure 6‑50 shows that, at the element in question, there is some variation in the orientation of
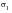
, but this is only when the stresses are very low. At this location, the stresses remain essentially aligned with the local x‑axis.
Figure 6‑51 shows that the stress state is not uniaxial, because
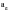
is not zero or constant. However, most of the variation is again at low stresses where the stresses are least important in fatigue terms. Overall, we can say that the loading at this location is essentially proportional (i.e., the principal stresses vary in a more or less fixed ratio and orientation). There is negative biaxiality.
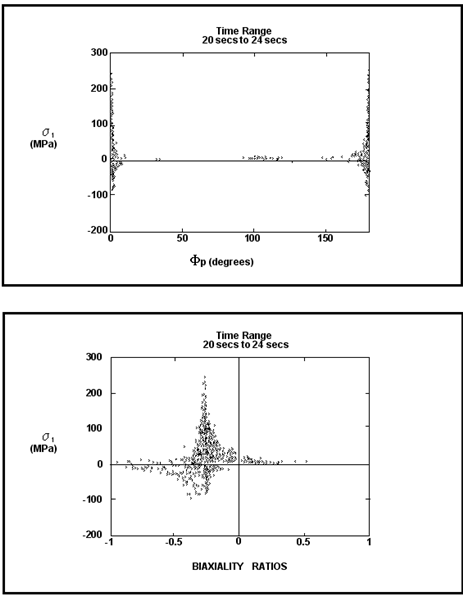
Figure 6‑50 Variation in Orientation of σ1
The next two plots once again illustrate essentially proportional loading, but this time with a positive biaxiality ratio.
Figure 6‑51 Multiaxial Stress State, Proportional Loading, Positive Biaxiality
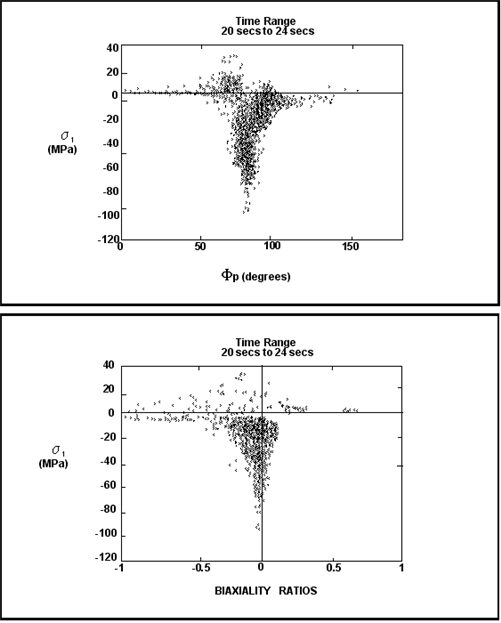
Figure 6‑52 shows a location where there is more variation in the principal stress directions. The biaxiality ratio plot shows that the dominant stress state is close to uniaxial. Note that the overall stresses are much lower here than in the previous examples.
Figure 6‑52 Variation in Principal Stress Directives
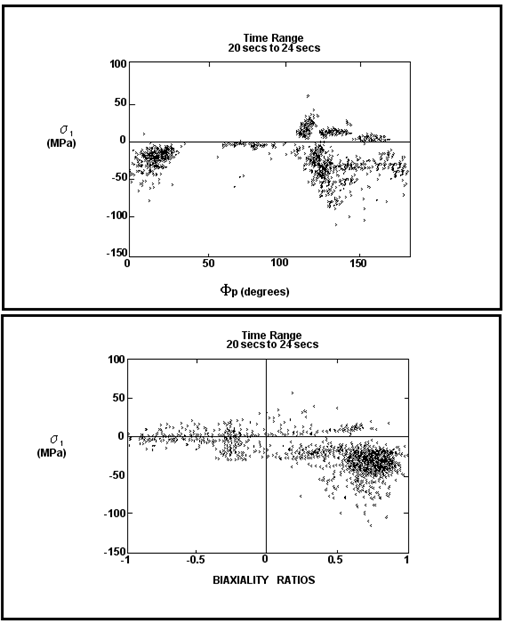
Figure 6‑53 illustrates the stress state variations at another location with comparatively small stresses. The loading here is essentially nonproportional because the orientation of the principal stresses exhibits considerable variation, and because the ratio of the principal stresses is not constant. Note that the stresses here are the elastic results from the FE analysis, with no correction for plasticity.
Figure 6‑53 Non-proportional Loading Stress State Variations
MSC Fatigue provides the following summary information about the stress state variations, in addition to the fatigue damage results for each node or element:
1. The mean biaxiality ratio.
2. The standard deviation of the biaxiality ratio.
3. The most popular angle.
4. The spread of angles for which the magnitude of the absolute maximum principal stress
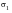
exceeds a gate value. The effect of this gate is to eliminate small stresses which are of less significance in fatigue terms. The default value of this gate is 0.2 times the UTS of the material. This is alterable by running FEFAT from the system prompt.
5. The range of the absolute maximum principal stress
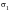
.
It is important to note that complex loading on a component does not necessarily lead to complex stress state variations at the critical locations. It is in the nature of fatigue that cracks tend to initiate at geometric features such as holes fillets and radii. These features tend to have 2 effects; they act as stress raisers, concentrating the stress, but they also often have the effect of lining the stresses up in a particular direction. Also, in many situations the geometry dictates that the stress state can only be uniaxial, for instance at the edge of a thin sheet.
Choosing an Appropriate Analysis Method
Fatigue consists of the initiation and growth of a crack, or growth from a pre-existing defect. Cracking is a directional process, and is driven by irreversible (plastic) strains. It follows that the nature and orientation of fatigue damage is a function of the stress and strain state variations. When the loading is not uniaxial there is a breakdown in similitude, and strictly uniaxial methods may be inappropriate. MSC Fatigue offers three main methods of dealing with multiaxial loading which are based on extensions to static yield theory. These are known as equivalent strain methods. When loading is uniaxial, it is normal to base fatigue life estimations on the values of the axial strains. When there is multiaxiality of loading the axial strain in the component or structure is replaced by an equivalent strain, which is considered to cause damage equivalent to the same axial strain in a uniaxial test specimen. The three equivalent strains used in MSC Fatigue are as follows:
1. The absolute maximum principal strain
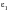
2. The signed Tresca parameter
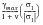
The signed von Mises strain (i.e., the von Mises strain with the sign of the absolute maximum principal stress), i.e.,
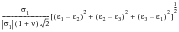
In addition, the user can select any component strain. In these equivalent strain methods, the selected parameter is cycle counted, then the Neuber correction is applied and damage assigned as if the strains were uniaxial. It is necessary to use the absolute maximum principal and the signed Tresca and von Mises parameters rather than their unsigned values because the latter give rise to truncation of cycles. This is illustrated in
Figure 6‑54. The example concerns a cylindrical notched specimen in fully reversed axial loading. Here, the principal stresses are ordered in the normal way. Mohr’s circles of stress at the notch root are shown for tension and compression loading. The first time history illustrated is the load time history, and the axial stress and strain will be similar in form.
Figure 6‑54 shows the maximum principal stress. This is always positive or zero, and the bottom half of the cycles is truncated.
Figure 6‑54 is a schematic plot of the von Mises stress. This is clearly of no use for the purposes of fatigue analysis, having too many cycles of the wrong size. We need a parameter which reflects the reversed nature of the loading and gives us a good representation of the reversed loading and number of cycles. This is provided by the last selection, the absolute maximum principal stress. The absolute maximum principal strain and the signed Tresca and signed von Mises will be similar in form.
When a “critical plane” method is used, instead of cycle counting an equivalent stress or strain parameter, MSC Fatigue calculates the direct strain on planes whose normals lie in the X-Y plane, at 10 degree intervals. It therefore makes 18 separate fatigue calculations and only reports the result for the plane with the shortest life. It is only suitable for surface resolved stress states, but overcomes some of the problems associated with the mobility of principal stresses. The down side of this method is the increased run-time.
Figure 6‑54 Example of Truncation of Cycles
The most appropriate method for crack initiation life predictions is a function of the prevalent stress state. Except where they start from pre-existing defects, cracks tend to initiate on planes of maximum shear, with crack growth being driven by shear strain initially before the crack turns into opening mode. Now biaxial loadings can be divided into two cases. These cases give rise to different patterns of early crack growth.
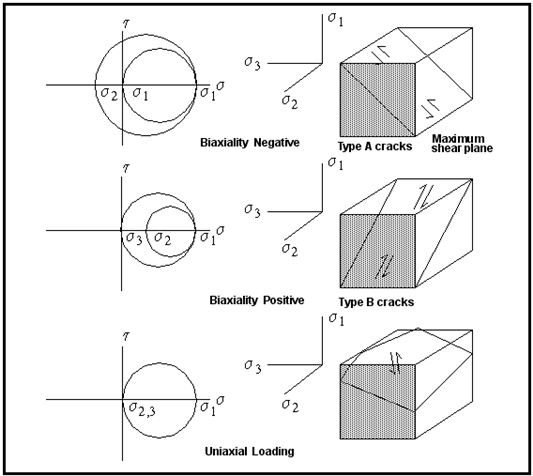
Figure 6‑55 Biaxiality Ratios
Figure 6‑55 (part a), the biaxiality ratio a
e lies somewhere between 0 and -1. A value of 0 represents the special case of uniaxial loading, and -1 represents pure shear. In this range, the maximum shear strain occurs on a plane intersecting the free surface (shaded) at right angles, and cracks in the initiation phase will tend to be driven along the surface in mode II. These are Type A cracks. In
Figure 6‑55 (part b), a
e lies between 0 (uniaxial loading) and 1 (equibiaxial loading). The plane of maximum shear now intersects the surface at 45 degrees, and cracks growing in mode II will be driven through the thickness of the material. These Type B cracks are therefore more damaging for a given range of maximum shear strain.
Figure 6‑55 (part c) above depicts the special case of uniaxial loading where the maximum shear plane is any plane at 45 degrees to the loading axis. Note that what we call “crack initiation” may actually include crack growth in shear and opening modes on more than one plane. Which type of crack behavior dominates “initiation” is material and stress-state dependent. The results of fatigue tests conducted under proportional loading at various biaxiality ratios suggest that the best parameter to use for loadings with 0>a
e>-1 (i.e., between uniaxial and pure shear) is the absolute maximum principal strain. For 0<a
e<1 (i.e., between uniaxial and equibiaxial) it is better, and more conservative, to use the signed Tresca parameter. This reflects that we are dealing with the more damaging type B cracks. The signed von Mises stress tends to give results that lie between the absolute maximum principal and the signed Tresca, except under uniaxial conditions, where all three should give the same result, and under equibiaxial conditions where the signed von Mises and signed Tresca should give the same result. There is a problem with loading where the value of a
e is around –1. Here the in-plane principal stresses are almost equal in magnitude but opposite in sign. The absolute maximum principal may “flip” between one and the other, and this may make it difficult to carry out a valid fatigue calculation. Under these circumstances, the MSC Fatigue angle spread results will indicate that the angle is moving through 90 degrees or more. The use may be able to get around this problem by using one of the strain components in conjunction with suitable fatigue data. These guidelines are summarized in the following table.
| Abs Max Principal Strain | Signed von Mises | Signed Tresca |
ae=-1
(pure shear) | Possible problems with mobility of principals
Use Critical Plane Option | | |
1<ae<0 | OK | Conservative | Very Conservative |
ae=0
(uniaxial) | OK | OK | OK |
0<ae<1 | Non-Conservative | Non-Conservative | OK |
ae=1 (equibiaxial) | Non-Conservative | OK | OK |
The comments above refer to situations where the local loading is proportional (i.e., the principal stresses are not directionally mobile and are proportional to one another). When this is not true, two problems are introduced:
1. It is no longer valid to assume that hardening is isotropic and that simple extensions of yield criteria can be extended to calculate elastic-plastic strains and stresses. A three-dimensional kinematic hardening model becomes necessary to model the material’s deformation behavior.
2. Fatigue cracking is directional. When the orientation of the principal stresses varies a great deal, linear damage summation will sum damage that actually represents cracking on different planes. In addition, in extreme cases it is possible to miss or truncate important fatigue cycles.
The further the situation deviates from proportional loading, the more caution the results should be treated with. MSC Fatigue’s biaxiality indicators — the angle spread and biaxiality standard deviation provide a means of quantifying the extent to which the local loading is nonproportional.
Biaxiality Correction Options
The uniaxial cyclic stress-strain curve is frequently used in fatigue analysis of stress concentrations, or notches, under unidirectional loading (tension or bending). However, the stress states at critical locations in many components subject to fatigue loadings are not uniaxial. For instance, even in a simple case such as a notched cylindrical bar in tension, the constraint on transverse strain often causes considerable notch root multiaxiality. In general then, the use of the Neuber method in conjunction with the uniaxial cyclic stress-strain curve is likely to generate values of stress and strain that are misleading, and if used as inputs to a fatigue analysis, potentially dangerous. Clearly, some means of taking into account the multiaxiality of stress and strains in necessary.
The following discussion addresses the description of material stress-strain responses in what will loosely be described as “proportional loading.” Strictly speaking, proportional loading means that the principal stresses remain in a constant ratio and the principal stress axes remain fixed in orientation. In practice, because multiaxial loadings are very often due to constraints (for instance at the root of a circumferential notch) the stress-strain state can be described more accurately by saying that the principal strains are in a constant ratio. For the purpose of this discussion, this condition will also be described as proportional loading, and because it is this condition that is closer to the majority of non‑uniaxial loadings that occur in practice, the methods describes model deformation under constant strain ratio rather than constant stress ratio.
The context for this discussion is the need in MSC Fatigue to calculate elastic‑plastic stresses and strains on the basis of linear elastic FE results, using methods based on the work of Neuber (Ref. 26). Two methods are described. Both are based on the extension of the von Mises yield criterion to predict post-yield stress‑strain behavior. The first, due to Hoffmann and Seeger (Ref. 27, 28), involves carrying out the Neuber correction on equivalent (von Mises) stresses and strains, and then calculating the required principal stresses and strains for the fatigue calculation using Hencky’s flow rules. The second, due to Klann, Tipton and Cordes (Ref. 29), takes the uniaxial cyclic stress-strain curve and calculates a new curve relating σ1 and ε1 which is a function of the principal strain ratio.
The following discussion assumes that we are dealing with stresses and strains at a traction free surface. This means that there are no non-zero direct or shear stresses normal to the free surface. The free surface is therefore in a state of plane stress. There are two non-zero principal stresses and they lie in the plane of the surface. For clarity, the following definitions are adopted:
σ1, ε1 | Principal stress, strain greatest in magnitude. |
σ2, ε2 | Other in-plane principal stress, strain. |
σ3, ε3 | Surface normal principal stress, strain. |
a | Biaxiality ratio s2/s1. |
ae | Elastic value of biaxiality ratio. |
Hoffmann and Seeger method - The treatment here just describes the implementation in MSC Fatigue. The Hoffmann-Seeger method can reasonably be applied when the selected Strain Combination is Absolute Maximum Principal or Signed Tresca. Application when using the signed von Mises is identical to the normal Neuber method.
The method assumes that the Neuber method can be applied using equivalent stresses and strains based on the von Mises values. The first step then is to take whatever parameter has been cycle counted and converted to equivalent strain. In order to deal with a random variable amplitude loading it is necessary to use a signed form of the von Mises strain. The subscript e denotes elastic values:
(6‑49)
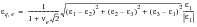
If the loading is proportional, then this value can be calculated from
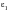
as follows:
(6‑50)
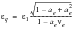
or from the Tresca parameter
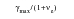
as follows, if a
e >=0:
(6‑51)
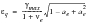
or if ae <0,
(6‑52)
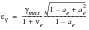
Of course
(6‑53)
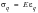
So far, all the stress and strain values are elastic. The Neuber correction is then carried out in the normal way, using the equivalent strain and stress values and the uniaxial cyclic stress-strain curve, i.e. assuming that:
(6‑54)
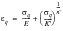
and that
(6‑55)
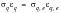
The effective (elastic-plastic) Poisson’s ratio for each cycle can now be calculated based on:
(6‑56)
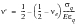
The elastic-plastic biaxiality ratio is calculated from:
(6‑57)
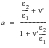
where the strain ratio is assumed constant
(6‑58)
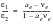
All the required principal stresses and strains can then be calculated:
(6‑59)
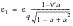
(6‑60)
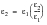
(6‑61)
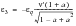
(6‑62)
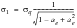
(6‑63)

enabling the elastic-plastic value of any desired combined stress-strain parameter to be calculated.
Parameter Modification Method (Klann, Tipton and Cordes) - The treatment here concentrates on the implementation in MSC Fatigue. Essentially, the equation
(6‑64)
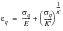
is used to calculate a series of corresponding values of
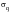
and
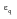
. For each pair of
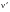
values, is calculated from:
(6‑65)
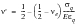
and a from
(6‑66)
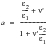
body
(6‑67)
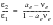
Pairs of values of
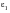
and
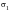
are then computed as follows:
(6‑68)
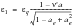
(6‑69)
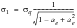
These pairs of values represent a cyclic stress strain curve for a particular biaxiality ratio ae. A new set of Ramberg Osgood parameters K” and n” is obtained by fitting the equation:
(6‑70)
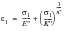
to the calculated points. E” is calculated explicitly from:
(6‑71)
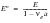
The modified parameters are used to carry out the Neuber correction in the normal way.
Multiaxial Cyclic Plasticity
When the loadings are non-proportional, the theories required to handle multiaxial cyclic plasticity become more complex.
Plasticity theory is a complex area. The treatment here is intended to provide an overview of the methods incorporated in the MULTIAXIAL option to MSC Fatigue without getting excessively mathematical.
There are three essential components of a plasticity model
1. A yield function
2. A flow rule, and
3. A hardening rule
The Yield Function: The yield function determines the limits of elastic behavior. The most popular yield function, which gives the best representation of the behavior of real materials, the von Mises or octahedral shear stress criterion. This can be expressed:
(6‑72)
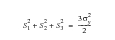
in terms of deviatoric stresses, or
(6‑73)
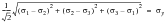
in terms of principal stresses. The parameter
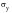
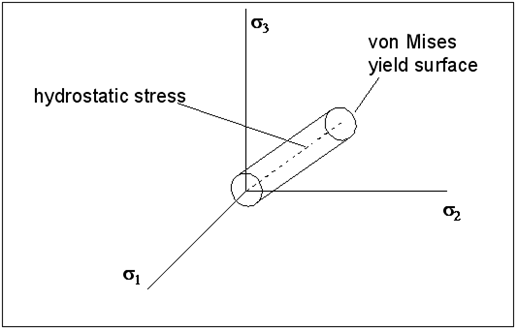
is the uniaxial yield stress. Graphically, the von Mises yield function appears as a cylinder in principal stress space, the axis of which represents the hydrostatic condition. The hydrostatic stress is assumed to have no effect on plasticity.
Figure 6‑56 von Mises Yield Function in Principal Stress Space
On a free surface, only two principal stresses are of concern, and the von Mises yield criterion appears as an ellipse.
Figure 6‑57 von Mises Yield Criterion on Free Surface
As long as the stress state remains within the yield surface or ellipse, there is no plastic deformation.
The Flow Rule: A basic assumption of plasticity theory is that the total strain can be partitioned into elastic components which can be calculated from Hooke's law, and a plastic component.
(6‑74)
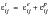
In incremental plasticity theory, the flow rule determines the direction of the plastic strain increment in relation to a given stress increment. Most plasticity models use the normality rule. This is based on potential flow, where the flow is determined by the partial derivatives of the potential function. If the potential function is assumed to be the yield function, then the direction of plastic flow must be normal to the yield surface. Mathematically this is expressed:
(6‑75)
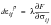
Where F is the yield function and
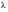
is a scalar quantity. The value of
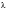
is given by:
(6‑76)
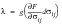
where g is related to the current slope of the stress-strain curve. The term in brackets is not allowed to take negative values. The value of g at any instant is determined by the hardening rule.
The Hardening Rule: The hardening rule determines how the yield point changes, taking into account the stress-strain curve and the loading history. For uniaxial loadings, the hardening rule is defined by the memory rule and Massing's hypothesis, which together dictate the current position of the yield point, and the current slope of the stress-strain curve.
When the loadings are multiaxial, this is not adequate - something is needed which tells how the yield surfaces will behave when the yield point is exceeded. There are two main classes of hardening rule - isotropic and kinematic.
In isotropic hardening, the yield surfaces grow when the initial yield point is exceeded. This is illustrated graphically here:
Figure 6‑58 Isotropic Hardening
Isotropic hardening is OK for predicting plasticity under monotonically increasing loading, but does not properly describe cyclic plasticity. For that we need a kinematic hardening rule.
In kinematic hardening rules, the yield surface translates when the yield is exceeded.
Figure 6‑59 Kinematic Hardening
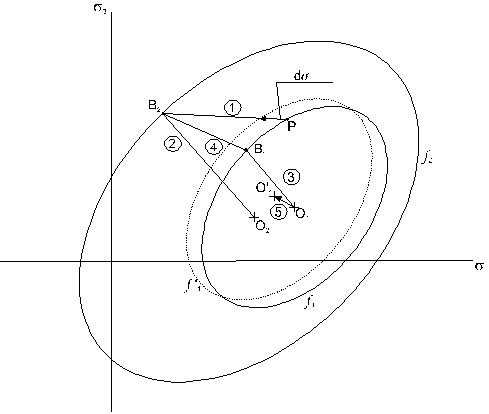
There are a number of possible kinematic hardening rules, and the hardening rule is the essence of most plasticity models. The hardening rule used in MSC Fatigue, both in the test-based module MMLF and the FE based module FEMLF, is the one originally suggested by Mroz (Ref. 45) and subsequently modified by Garud (Ref. 46). This is a multi-surface model, where there are a number of initially concentric yield surfaces. The inner surface corresponds to the elastic limit. Within this surface, only Hooke's law (generalized to 3 dimensions) is used. The other surfaces correspond to the changes of slope in a linearized cyclic stress strain curve.
Figure 6‑60 Linearized Cyclic Stress-Strain Curve
In the software, 40 surfaces are used, and the result is quite a smooth cyclic stress-strain curve. The curve is determined automatically from the Ramberg-Osgood equation.
When a loading is applied, the loading point can be traced within this diagram. So long as the loading point remains within the inner ellipse, there is no plasticity. When the loading point touches this ellipse, it must move. The direction in which it translates is described graphically in the following diagram:
Figure 6‑61 Translation of Ellipse when Plasticity Occurs
In this diagram, only two surfaces are drawn. The stress increment is extended from the surface to find the point B2 where it intersects the next surface. The center of the larger surface is joined to this point. A line is drawn parallel to this line from the center of the smaller surface to find where it intersects the smaller surface at B1. The ellipse then translates in the direction B1 B2 until the end of the current loading increment lies on the surface of the inner ellipse. This rule may sound complicated, but it ensures that when the ellipses meet, they do so tangentially. When two or more ellipses meet, they move together. The outermost active ellipse determines the current slope of the stress-strain curve.
Multiaxial Non-Proportional Notch Correction Procedure
When making local strain calculations on the basis of elastic pseudo stresses or strain, a notch correction procedure is required in order to estimate the local elastic-plastic stresses and strains that are required. When the loading is uniaxial or proportional, the Neuber method, or a variation such as the Hoffmann-Seeger method, works quite well. These methods essentially apply the Neuber equation:
(6‑77)

together with the equation for the stress-strain curve for each cycle or reversal. However, when the loading is non-proportional, this is no longer adequate, because the stress response to a given strain reversal (and vice versa) is path dependent. We therefore need an incremental formulation. An incremental version of the Neuber rule for non-proportional loadings might look like this:
(6‑78)

This must then be combined with a non-proportional cyclic plasticity model such as the Mroz-Garud model.
Additionally some assumptions are required in order to reach a solution, e.g. that the ratios of the increments of strains, stresses or total strain energy in certain directions are the same for the elastic as the elastic-plastic case. The method used in MSC Fatigue is based on the total strain energy (strain energy plus complementary strain energy). This method is described in more detail in (Ref. 69).
Multiaxial Safety Factor Analysis
Multiaxial fatigue is a term referring to fatigue of components under complex stress states. High-cycle multiaxial fatigue deals with components which during their life time are expected to experience very large number of cycles. Due to the nature of the fatigue process, it is not possible to make realistic finite life predictions for components that may experience very large numbers of major loading cycles during their service. For instance, a typical car engine running at 3000 rpm only has to run for 21 days before many engine components such as connecting rods or pistons have experienced 108 cycles. This number could easily be achieved within 30,000 miles. Such components are therefore designed for infinite life. Other examples include crank shafts, propeller shafts, and rear axles. In these components, it is not necessary to quantify the amount of fatigue damage, but just to consider if any fatigue damage will occur during the load history.
For high-cycle multiaxial fatigue, actual quantities of fatigue damage are not considered. Instead, the loading history is examined to determine only if damage occurs at any moment. If damage does occur, then the component does not have infinite life. The high-cycle criteria considered can also be used to calculate a safety factor of a component if infinite life is determined.
In cases of high-cycle fatigue, the complex stress states in the loading history are important to consider in order to accurately predict fatigue life. A simple uniaxial fatigue method is not sufficient and can produce non-conservative results. A multiaxial fatigue limit or endurance limit criterion is required.
High-Cycle Multiaxial Fatigue Theories
Several methods have been developed to calculate a fatigue limit in the high-cycle fatigue (HCF) regime with significant multiaxial loadings. Diboine (Ref. 70) classifies these methods according to the basis of calculation:
• Empirical
• von Mises
• Tresca
• Micro-structural
The empirically-based fatigue criteria require testing of a specific material in a loading configuration similar to that of interest in order to produce a numerical fit to the data and make further predictions. This defeats the purpose of using fatigue predictions, and therefore this type of method will not be considered further.
Von Mises-based criteria were prevalent early in the studies of high-cycle fatigue, the Sines and Crossland criteria being quite well-known. However, von Mises is a deformation criterion which does not consider the plane of maximum shear stress range. Fatigue cracks have been observed to initiate and grow initially along these planes of maximum shear stress.
The above observations lead to the more intuitive Tresca-based high-cycle fatigue criteria. Findley reported early 1959 on Tresca-based predictions, but McDiarmid’s Tresca-based criterion introduced in 1987 appears to be widely accepted and well-known.
Microstructural approaches to high-cycle fatigue have also become more common in recent years. These approaches consider the stabilized, microscopic stresses in calculations of fatigue damage. Dang Van first introduced this type of approach in 1973, but his modified approach proposed in 1987 is easier to use and provides better correlation.
McDiarmid Criterion
The McDiarmid criterion (Ref. 71)(Ref. 72) has several significant features. It is a critical plane approach, where the critical plane is defined as the plane of maximum shear stress. The fatigue criterion is based on two loading parameters:
• Shear stress amplitude
• Maximum normal stress for the entire loading history on the plane on maximum shear stress
Another feature of the McDiarmid criterion is that it considers Case A and Case B cracking separately in calculating for fatigue damage. Case A cracking is along the surface, as in torsion; while Case B cracking is into the surface, as in bending.
Fatigue Limit: The fatigue limit according to McDiarmid can be expressed in the following form:
(6‑79)
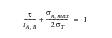
τa | | shear stress amplitude (half the maximum range of shear stress) |
tA, B | | reversed shear fatigue strengths for Case A and B crack growth |
σn, max | | maximum normal stress for the entire loading history on the plane of maximum shear stress amplitude |
σT | | tensile strength |
Any value of the left-hand side of this equation exceeding 1 indicates that damage occurs. This fatigue limit can be displayed graphically in a plot of
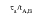
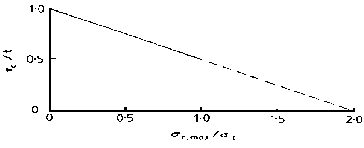
vs.
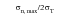
:
Figure 6‑62 Fatigue Limit, τa / tA, B vs. σn, max / 2σT
Any loading that goes above the line is considered to cause damage, and the component does not have infinite life.
The reversed shear fatigue strength for Case A cracking, tA, is the reversed torsion fatigue strength of the material. The reversed shear fatigue strength for Case B cracking, tB, is found from a Case B cracking test case (3).
If you have only uniaxial data, one way of estimating these values is to consider the case of the uniaxial fatigue limit where the stress amplitude is
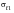
and assuming that the uniaxial case is the point where Case A or Case B can occur to write:
(6‑80)
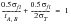
so that tA, B are given by:
(6‑81)
Implementation: Both Case A and Case B planes are searched to find the plane with the maximum value of shear stress
. Both Case A (
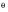
= 90 degrees) and Case B (
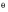
= 45 degrees) are considered, and the orientation
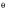
of the planes is varied by 10 degree increments over a 180 degree range. The maximum shear range for each plane is calculated by the difference of the maximum and minimum values of shear stress for the loading history. The McDiarmid criterion calculations are then performed for the planes of maximum shear stress range. Because the fatigue limit criterion is expressed:
(6‑82)

a safety factor can be defined:
(6‑83)
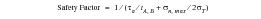
This safety factor is calculated by the MSC Fatigue program FEMLF and reported in the .fos file.
Note: | The McDiarmid method is restricted to free surface stress conditions. |
Dang Van Criterion
The Dang Van Criterion is classified as a ‘micro-structural’ method because it considers stresses and crack initiation at the local level. The stabilized local residual stresses are calculated by means of an iteration in which convergence assumes a stabilized state, a state of elastic shakedown. These stresses are used to examine microscopic stresses in the material from given macroscopic stresses.
Dang Van (Ref. 73)(Ref. 74) describes crack initiation (damage) to occur when some function of microscopic stress, f, is greater than or equal to zero at any time in a stabilized cycle. The following notation is used:
(6‑84)
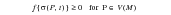
M | | a point of interest/stress concentration on a component (notch, fillet) |
V(M) | | An elementary representative volume around M |
P | | A point in V(M) where a grain(s) is critically oriented |
σ(P,t) | | A microscopic stress tensor at location P at time t |
Fatigue Limit: Dang Van chooses this function of stress to be linear, and utilizes the shear stress and hydrostatic tension at any given time:
(6‑85)
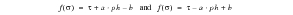
τ | | microscopic shear stress at a given time |
ph | | microscopic hydrostatic tension at a given time |
a | | sensitivity to hydrostatic tension |
The shear fatigue limit, t, and bending fatigue limit, f, may be used to estimate a and define b in the following way:
(6‑86)a = 3(t - 0.5f) / f
(6‑87)b = t
This formulation ensures that the Dang Van criterion reduces to the uniaxial fatigue limit under uniaxial conditions. If you only know the uniaxial fatigue limit then try b=t=0.5774f which means a=0.231.
The Dang Van method can be used to define a safety factor:
Safety Factor = 1/d where
(6‑88)d = Max [τ(t) / (b - a*ph(t))]
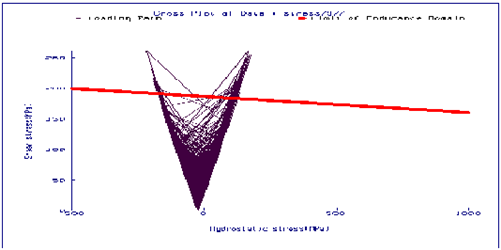
This function establishes the Dang Van Endurance Domain shown below:
Figure 6‑63 Dang Van Endurance Domain
A loading path (defined by the microscopic shear stress and hydrostatic tension) is shown on the above plot. Damage occurs when a loading line crosses the endurance limit line (safety factor =1). In this case the loading path does cross the line, so the safety factor will be less than 1. If a loading line does not cross the endurance limit, failure will not occur for any number of cycles on this loading line.
Implementation: Shown below are the steps of the Dang Van method:
For a given point M,
1. Evaluate the macroscopic stresses (
, a stress tensor) at point M for each time t where
.
θ is the smallest interval such that
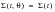
, i.e.
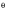
is one block.
2. Split macroscopic stresses into hydrostatic and deviatoric components:
Hydrostatic component, PH(t):
(6‑89)

Deviatoric component, Sij(t):
(6‑90)
for trace elements only
3. Determine the microscopic deviatoric residual stress tensor, dev ρij*:
The element values of the tensor dev ρij* are the same throughout the cycles. These values are determined through an iterative process.
4. Determine deviatoric parts of localized stresses:
(6‑91)
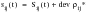
(6‑92)Determine microscopic shear stress,
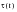
:
(6‑93)
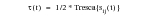
where the Tresca is just the difference between the two largest principal stresses at this location and time.
5. Determine Damage Parameter, d:
(6‑94)
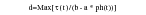
The maximum is taken over all times.
6. Failure Criterion:
If d < 1, fatigue failure will not occur. Safety factor = 1/d
This process is all relatively straightforward, with the exception of the determination of the microscopic deviatoric residual stress tensor dev
. This is explained as follows.
Determination of Microscopic Deviatoric Residual Stress
The determination of the so-called “Microscopic Residual Stress”
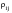
* is somewhat complex in nature. It is based on the supposition that on a microscopic level, in critical grains there will be some plastic deformation even below the fatigue limit and there will be shakedown leading to the development of a residual stress. The way this residual stress is calculated is by a combination of isotropic and kinematic hardening. This process starts with the definition of an initial yield surface, centered on zero macroscopic stress. Successive loading points from the stress history are applied. When the loading point exceeds the yield stress, the yield surface moves to ensure it still contains the current loading point (kinematic hardening) and also grows (isotropic hardening). The rate at which the yield surface grows is determined by the hardening parameter. As the loading history is repeated, the surface grows until it reaches a stabilized condition in which it encompasses the entire loading history and there is no further movement or growth. The displacement of the center of the yield surface from the center of the original yield surface defines the microscopic residual stress. This process is illustrated in the following diagram.
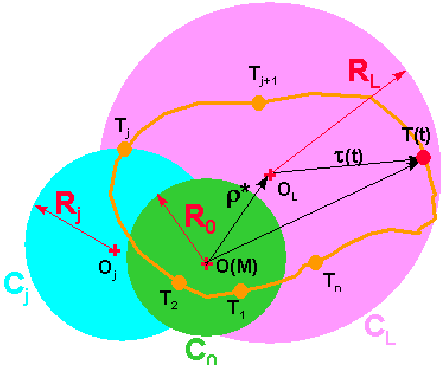
Figure 6‑64 Definition of Microscopic Residual Stress
Notice that this is a 2-dimensional representation of the process. In practice the process can be thought of as an iterative method for finding the center of a 9‑dimensional hypersphere which will encompass the whole loading history. The “hardening parameter” is simply a numerical parameter which controls the speed at which convergence is approached. Larger values of this parameter will give more rapid convergence but may result in some overshoot.
Note: | The Dang Van method is a full 3-D method and is applicable to 2-D and 3-D stress states irrespective of coordinate system. |