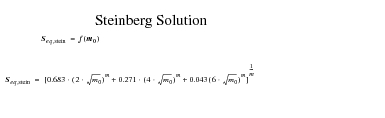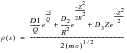XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> Vibration Fatigue Theory
Frequency based techniques for fatigue life prediction are now available to the analyst/designer through the Frequency Life Fatigue Estimation (MFLF and FEVIB) modules of the MSC Fatigue software package. This section is intended to provide the required technical background for the practical designer. Where more detailed information is required the reader is referred to the list of references provided in
References (Ch. 16).
A Time or Frequency Approach?
Structural design can be conveniently categorized as either testing or analysis. By testing we usually mean the experimental measurement of stresses or strains on a laboratory or test track prototype. Or alternatively, testing might involve the measurement of noise or vibration rather than stresses. By analysis we usually mean the computation of structural response using a technique such as Finite Element Analysis (FEA).
In general there are two alternative options (or domains) which can be used for such testing or analysis. Conventionally the analysis might be carried out in the time domain, where all inputs loadings and output responses are specified as time sequences or derivatives thereof.
For example, the stress history induced in a critical component of a car chassis while being driven over a road surface might be experimentally measured, or estimated at the design stage using appropriate analysis programs.
An alternative approach is to perform the analysis in the frequency domain. In this case all loadings and output stress responses are represented as plots of energy at different frequencies.
A
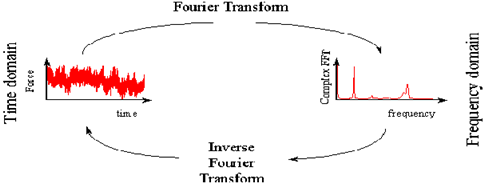
Power Spectral Density Function (PSDF or PSD) is the most common way of representing the loadings or responses in the frequency domain. The transformation between time domain, i.e., the time history of the loading, and the frequency domain, i.e., a PSD, should not trouble the reader. The PSD simply shows the frequency content of the time signal and is an alternative way of specifying the time signal. It is obtained by utilizing the
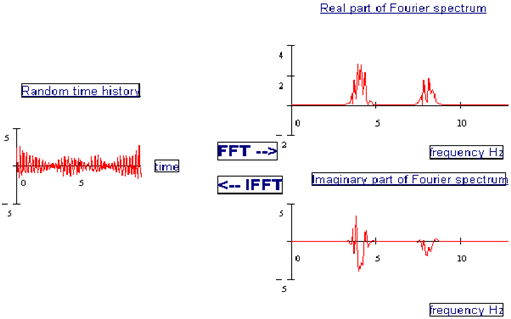
Fast Fourier Transform (FFT). Figure 8‑38 shows this equivalence for a typical structural response signal.
Transforming from the frequency domain to the time domain is also a relatively easy task which can be done using the Inverse Fourier Transform (IFT). However, when transforming in this direction the random phase angles attributable to each frequency component (which have not been kept when converting to the frequency domain) have to be generated or regenerated. This can be done such that a statistically equivalent signal can be reproduced.
Figure 8‑38 PSDs and the Transformation Between Time and Frequency Domains
Comments on Time versus Frequency Domain Approach
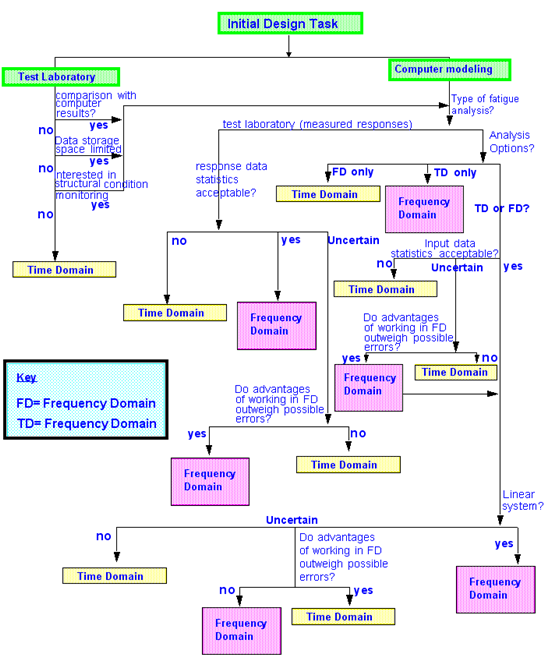
This explanatory text assumes that any prospective designer will be approaching either the task of laboratory test measurements or, alternatively, computer-based design. For each type of task a number of key questions may need to be addressed in order to decide if frequency domain techniques are the appropriate route. These questions are discussed below.
• Q. I am undertaking laboratory tests. Do I need to compare my results with, for instance, FEA results?
An example from the automotive industry demonstrates that frequency based FEA can be a powerful qualitative as well as quantitative tool for the reliability assessment of certain components. If this is likely then frequency based tests and fatigue calculations may be appropriate.
• Q. Are data storage problems likely to be an issue, either in terms of hard disk space or speed of acquisition?
An acquisition rate of one tenth of that for time domain measurements can usually capture the frequency domain data required for a fatigue analysis with the same level of accuracy. Furthermore, there can also be a significant reduction in storage space required for the frequency domain data. This is because PSDs are significantly easier to obtain, and store, than long time histories.
• Q. As part of the testing work being undertaken is any structural condition monitoring required, or beneficial?
Frequency based measurements are very useful for determining any changes in structural behavior or performance. Any change in the system transfer function (see later) is a useful indicator that some structural change has taken place such as the growth of a crack. If such structural monitoring is likely to be beneficial then frequency based tests and fatigue calculations may be appropriate. Alternatively, a vibration analysis may be the required objective in order to determine whether a structure, such as a car body, is acceptable. In this case, if fatigue is also an issue a frequency based analysis may well be appropriate.
• Q. What type of fatigue analysis is being undertaken?
Is the fatigue calculation being undertaken with measured frequency domain data, or is the frequency domain data being generated using a computer analysis package? The answer to this question has a significant bearing on the number of assumptions which need to be considered before proceeding with a frequency based fatigue analysis. If, for instance, a PSD of structural response (stress or strain) has been measured, then only the characteristics of this measurement are important. If a structural computer analysis such as an FE analysis is being undertaken then the characteristics of the structural system also need to be considered.
• Q. What are my analysis options?
It may be the case that, because of the nature of the structure you are analyzing, your analysis route is already determined. For instance, many deep water offshore oil platforms can only be satisfactorily designed in the frequency domain, thereby producing frequency domain results. In this case a frequency based fatigue calculation is the only option. Alternatively, the nature of the fatigue damage mechanism, or the structural system, may determine that only a time based approach is applicable. If either of these scenarios is true then the correct approach is already defined. More usually there is a choice, or perhaps both approaches in parallel are appropriate. In which case the additional questions below need to be addressed.
• Q. If I am directly measuring my response data (stress or strain) is it stationary, Gaussian and random?
These are probably the issues which cause the most concern to design engineers.
Firstly, on the question of how Gaussian (sometimes referred to as ‘normality’) particular data is. If we calculate the percentage of time that response data spends within a particular stress bin and plot this as a probability density function (PDF) we require that its PDF (probability density function) follows the Gaussian bell shape. Fortunately there is a theoretical explanation to explain why nearly all engineering components and structures exhibit Gaussian behavior. This is called the Central Limit Theorem. This states, in very general terms, that the response of any system will be Gaussian as long as the number of processes contributing to this system response is reasonably large and that no one process dominates. This is true even if the individual processes are not Gaussian. Practical fatigue calculations have shown that the fatigue predictor tool MFLF is quite robust to some variation from a strictly Gaussian signal. However, this is an issue which should be assessed before proceeding with any frequency based calculations.
If the signal is stationary, it means that the general characteristics, such as rms, don’t change with time. For most engineering processes this is true. Furthermore, even when the signal characteristics are changing slowly with time, the complete response process can usually be broken up into a number of shorter stationary processes. An example of this, for offshore data, is given in the Case Studies Manual. This is again something which should be assessed before proceeding with any frequency based calculations.
Finally, and perhaps most importantly, is the signal random. If it isn’t then a time based approach is probably appropriate. For instance, if a small number of transients dominate the fatigue damage, then it is almost impossible for a frequency based fatigue predictor, such as MFLF, to properly identify these. This is perhaps an example, such as that referred to in the Central Limit Theorem, where one process dominates the rest. If such transient or deterministic inputs are relatively small, in comparison to the rest of the response data, then a frequency based calculation may still be possible.
• Q. What determines if any data conforms to these assumptions?
The only real test, in the context of a fatigue calculation, is how accurate the estimated fatigue life result is. Case studies have shown some results for wind turbine blade response data which helps us to make some practical judgments about this. These results tell us that unless a dominating deterministic component, such as a transient, is present in the signal then MFLF is surprisingly robust to small levels of non-stationarity and non-Gaussianality. However, real care has to be taken with transients and deterministic components.
• Q. Do advantages of working in the frequency domain outweigh possible errors?
If a frequency based fatigue predictor is coupled up with a frequency based load predictor, such as an FEA program, then a designer has the ability to undertake rapid design optimization. He may then choose to use a time based calculation for the final ‘proving’ analysis calculation. In such a case, any loss of accuracy involved in working in the frequency domain is far outweighed by the increased design capability. This is therefore something which should be carefully considered.
• Q. If I am using data to perform a frequency based FEA, and subsequent fatigue calculation, is the data stationary, Gaussian and random?
There are some circumstances when the response of a structural system will be Gaussian even if the input is not. However, in general, if you wish to perform a frequency based analysis you should place the same requirements on the input loading data that you would on any response data. Subject to system linearity (see below) this will ensure the response data is satisfactory.
• Q. Is the system linear?
Before we can consider this we need to consider, in more detail, what is involved in computing a structural response estimate using, for instance, an FEA package. In order to obtain the output (PSD) response of any system we need its transfer function. This transfer function then obeys the following:
There are a number of experimental and analytical ways of obtaining the transfer function. The simplest and easiest method to visualize is the so-called sine sweep. Using this method the response of a system to a particular sine wave of a particular magnitude is noted, the frequency of the sine wave is then incremented by a small amount and the magnitude of response is noted again. By repeating the process a response vs frequency plot for all frequencies of interest can be produced which can then be used directly to evaluate the transfer function.
An alternative way of obtaining the transfer function is to apply an input of white noise which is an input that has a flat-topped PSD over all frequencies of interest. The response to this random input can be used directly to obtain the transfer function by dividing the output PSD by the (constant) height of the white noise input PSD.
These experimental techniques have their analytical equivalents. For instance, a series of unit load steady state (harmonic) analysis computations can be used to obtain the required transfer function ordinates. Alternatively a time domain analysis can be performed using white noise as the input and the response obtained can then be used to obtain the transfer function. It should be clear from the above that the transfer function is a characteristic of the system or structure. It is not until the transfer functions have been established that the actual loadings are applied. This highlights the usefulness of spectral techniques because the computational effort involved in computing the responses is trivial compared to that of computing the transfer functions themselves.
Figure 8‑39 Frequency or Time Domain Decisions?
An Introduction to Random Process Theory
This section introduces random processes to facilitate an understanding in the theory behind vibration fatigue analysis. It is not intended that this serve as a definitive reference on the subject but rather a primer on the concepts involved. The description starts with an account on the theory of the Power Spectral Density Function (PSD) and progresses to cover single random processes and then multiple, partially correlated random processes.
Representing a Time Signal Using Fourier Series
Any periodic time history may be represented by the summation of a series of sinusoidal waves of various amplitude, frequency and phase. This is the basis of Fourier series expansion, a detailed explanation is given in (Ref. 100.). The Fourier series expansion of a time history y(t) is often expressed by
(8‑1).
(8‑1)
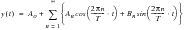
and
The terms A
0, A
n and B
n are termed Fourier coefficients and provide information on the frequency content of the time history. A
0 represents the mean of the time history while A
n and B
n represent the amplitude of the various cosine and sine waves which when added together comprise the time history.
Figure 8‑40 shows the Fourier series expansion for a particular saw tooth time history. By the third summation the expansion is seen to give a reasonable representation of the original time history. Further summations improve the representation.
Figure 8‑40 Fourier Series Expansion
The integrals within A
n and B
n effectively act as a filter and extract the amplitude of a cosine or sine wave of frequency n/T Hz. from the time history. This is accomplished using the relationships given in
(8‑2).
(8‑2)
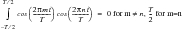
The Complex Fourier Series
In practice the Fourier coefficients A0, An and Bn prove very cumbersome to manipulate algebraically. Complex number theory helps with this aspect as all three coefficients may be replaced by one complex coefficient Cn.
The first thing to realize is that the sum of a cosine and sine wave results in a sinusoidal wave of amplitude r and initial phase angle

provided both waves have the same frequency.
Figure 8‑41 shows the summation of a cosine and sine wave with amplitudes A and B respectively and frequency
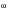
.
Figure 8‑41 Summation of Cosine and Sine Waves
The amplitude r and initial phase angle

of the resultant sinusoidal wave can be obtained using the relationship given in
(8‑3).
(8‑3)

It is convenient to express the Fourier coefficients A
n and B
n in terms of the complex coefficient

where
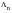
= A
n - i.B
n. The amplitude r and phase angle

can then be obtained from the 'magnitude' and 'argument' of the complex coefficient as shown in
(8‑4).
(8‑4)

Having expressed the amplitude and initial phase of the sinusoidal wave in complex terms it is now convenient to utilize the complex form of the exponential function to represent the frequency term. This technique is explained in (Ref. 100.), and follows the relationship given in
(8‑5).
(8‑5)
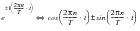
Using these relationships the original Fourier term A
n cos
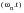
+ B
n sin
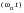
can be replaced with the complex number representation given in
(8‑6).
(8‑6)
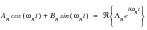
(8‑1) may therefore be written in complex form by
(8‑7).
(8‑7)
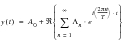
The expression may be simplified further by the introduction of negative frequencies. These have the effect of cancelling the imaginary components in
(8‑7) without using the
function. Using the concept of negative frequencies
(8‑7) can be expressed as
(8‑8).
(8‑8)
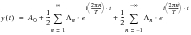
Changing the limits of the summation the Fourier coefficients A
0 and
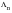
can be replaced with the single complex Fourier coefficient C
n as expressed in
(8‑9).
(8‑9)
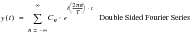
(8‑9) is said to be double sided because it uses both positive and negative frequencies to represent the Fourier coefficients.
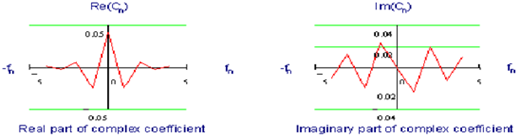
Figure 8‑42 shows a plot of the Real and Imaginary parts of the complex Fourier coefficients C
n obtained from the expansion of the saw tooth wave plotted with respect to frequency n/T Hz.
Figure 8‑42 Plot of Real and Imaginary Parts of Complex Fourier Coefficient
The complex Fourier coefficient C
n is used to obtain the amplitude and phase of the n
th sinusoidal wave using the formulation given in
(8‑10).
(8‑10)

Where C-n = An+i Bn and Cn = An-i Bn.
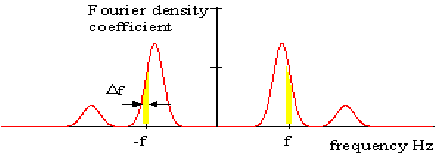
The Fourier Density Coefficient
The previous section introduced the complex Fourier series expansion, we are particularly interested in obtaining the complex Fourier coefficients C
n and these are discussed in this section. Each Fourier coefficient C
n is obtained for a frequency of n/T Hz, the frequency interval between each coefficient

f is therefore 1/T Hz. This causes problems as the frequency at which the coefficients are calculated is dependent on the period T chosen. It is common practice to normalize the coefficients to eliminate the dependence on T. The normalized coefficients take the form of a 'density function' and the Fourier coefficient is obtained from the area under the density curve for the range
f in question. This is shown in
Figure 8‑43.
Figure 8‑43 Fourier Density Coefficients
Using this normalization the complex Fourier series expansion given in
(8‑9) can be expressed by
(8‑11).
(8‑11)
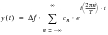
The amplitude and phase of the sinusoidal wave with frequency f is now obtained by taking the magnitude and argument of the area under the density curve in the region
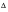
f. The function behaves much like a Probability Density Function.
If
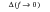
then the summation given in
(8‑11) can be expressed in integral form and c
n can be written as y(f). Changing the limits of integration between
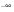
and
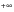
the complex Fourier series is now expressed in integral form as
(8‑12). This is known as the Fourier Transform Pair. For future reference in this chapter y(f) shall be called the “Fourier Spectrum.”
(8‑12)
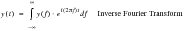
It is worth noting that many references use a different normalization to that given above, an alternative normalization is to use the square root of the period.
The Fourier Transform Pair
The 'Fourier Transform Pair' was derived earlier in integral form and is expressed in
(8‑12). It is now apparent that a time history y(t) can be completely expressed by the “Fourier Spectrum” y(f). The Fourier spectrum can therefore be thought of as another 'frequency domain' in which a time history may be expressed. In this sense, y(f) implies a description of the time history 'y' in the frequency domain 'f'. The 'Fourier Transform Pair' effectively transforms between the two domains.
In addition to the integral form, the 'Fourier Transform Pair' can also be described in a discrete form. This is particularly beneficial as most measured time histories are obtained in a discrete, digitized form with values taken over equally spaced intervals in time. In these circumstances the integral form is difficult to process and it is desirable to perform some numerical routine on the measured time history to transform it into the frequency domain. This transform is known as the “Discrete Fourier transform.” The result obtained from a discrete transformation will tend to the result obtained from an integral transformation as the sample length and sampling frequency increase.
Cooley and Tukey (Ref. 101.) devised a very rapid discrete Fourier transform algorithm in 1965. It is known as the “Fast Fourier Transform (FFT)” and has a reverse process called the “Inverse Fourier Transform (IFFT).” There are a number of derivatives of these each using a different normalization. The discrete form of
(8‑12) is defined in
(8‑13).
(8‑13)
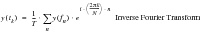
Fourier Analysis of Random Time Histories
Under certain circumstances, random time histories may be expressed in the frequency domain. By definition, a random time history cannot be periodic. However, provided the time history is taken from a 'stationary random process' then it may be expressed in the frequency domain. A stationary process is defined as a process whose statistics are not affected by a shift in the time origin. (i.e. the statistics of a time history X(t) are the same as a time history X(t +
) for all values of
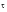
) For non-stationary processes the statistics obtained from a sampled time history would not be representative of those of the whole random process as these would be continuously changing. Priestley, (Ref. 102.), discusses stationarity at length. The analysis of non-stationary random processes is not considered in this text.
Figure 8‑44 illustrates the application of the Discrete Fourier Transform pair to a random time history taken from a stationary random process.
Figure 8‑44 Frequency Domain Representation of a Random Time History
For real time histories the Fourier transform is symmetric about zero Hz. A Double Sided Spectrum is said to be symmetric if the relationships given by
(8‑14) are satisfied.
(8‑14)
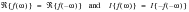
It is usual to express a symmetric spectrum as a “Single Sided Spectrum.” The “Single Sided Spectrum” contains the same information as the “Double Sided Spectrum” but is often more convenient to use as negative frequencies are not considered. All measured time histories can be expressed as a Single Sided Spectrum. The relationship between single and double sided spectra is given by
(8‑15).
(8‑15)
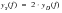
Figure 8‑45 illustrates the Single Sided Spectrum of the random time history given above.
Figure 8‑45 Single Sided Fourier Transform
Power Spectral Density Function (PSD)
We have considered the representation of a stationary random time history in the frequency domain. Often it is more beneficial to have a statistical description of the random process rather than the deterministic one. For this purpose, the “Power Spectral Density (PSD)” function is useful. A good historical and qualitative description of what the PSD actually is is given by Spence (Ref. 103.). The PSD gives a statistical representation of a stationary random process in the frequency domain. It is defined such that the area beneath the PSD represents the mean square amplitude of the random process. Many design standards, such as the ESDU papers (Ref. 104.) on wind turbulence and the design standards for offshore sea conditions, express the statistical properties of random processes in terms of PSDs. Using these in conjunction with a linear structural model allows PSDs of structural stresses and deflections to be calculated and fatigue life estimates to be obtained. These subjects are covered later in the thesis. The PSD is used in the same way as the Fourier Density spectra. The mean square amplitude of a sinusoidal wave of frequency f can be obtained by taking the sum of the area under the PSD at +f and -f over the interval
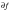
as
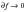
. This is illustrated in
Figure 8‑46.
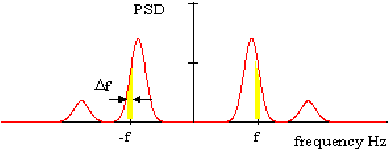
Figure 8‑46 Double Sided Power Spectral Density (PSD)
PSDs may be complex and expressed as both double or single sided spectra in the same way as the Fourier density spectra. The relationships given in
(8‑14) and
(8‑15) hold for single and double-sided PSDs. PSDs calculated from measured time histories will always be real. The real part of a complex PSD S(f) is known as the co-spectral density function and the imaginary part as the quad-spectra density.
We will now consider the transformation from a single sided Fourier Density Spectra to a single sided PSD. The mean amplitude of the component sinusoidal waves over a frequency range
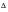
f is obtained from the Fourier spectra by taking the modulus of the area under the curve as expressed in
(8‑16).
(8‑16)
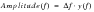
The area under a PSD represents the mean squared amplitude of the component sinusoidal waves where
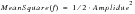
. We can equate the mean square amplitudes calculated from the PSD and the Fourier spectra and hence determine the transformation between the two, this is derived in
(8‑17).
(8‑17)
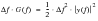
The double sided PSD is determined in a similar fashion, the results are summarized in
(8‑18).
(8‑18)
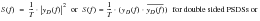
Where yD(f)* is the complex conjugate of yD(f).
Both the modulus and complex conjugate forms of the transformations are correct however it is mathematically beneficial to use the complex conjugate form. It is also worth noting that many books adopt a different notation for the double and single sided PSDs. In this text the notation S(f) and G(f) is adopted for the double and single sided spectra respectively.
Earlier we commented on the use of different normalizations applied to the Fourier transform. It is quite common to see the
normalization being used and this changes the formulation expressed in
(8‑18) to the form
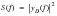
or
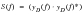
. The normalization chosen for the Fourier transform is not important provided that the resultant PSDs are the same.
The PSD offers considerable information about the statistics of the random process. By definition the area under the PSD represents the mean square amplitude of the time history. For zero mean time histories the standard deviation may be calculated from the square root of this. Other statistical properties may be obtained using the spectral moments of the PSD. The n
th spectral moment m
n of a PSD is defined by
(8‑19).
(8‑19)
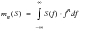
The key statistical properties listed in
(8‑20) were derived by S.O. Rice (Ref. 99.) in 1954. These properties become important when considering the fatigue life of a structure. This is explained in detail in
Characterization of Structural Response in the Frequency Domain, 710.
Standard deviation | |
Expected number of zero crossings | |
Expected number of peaks | |
Irregularity factor | (8‑20) 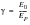 |
The appearance of the PSD plot also conveys much information,
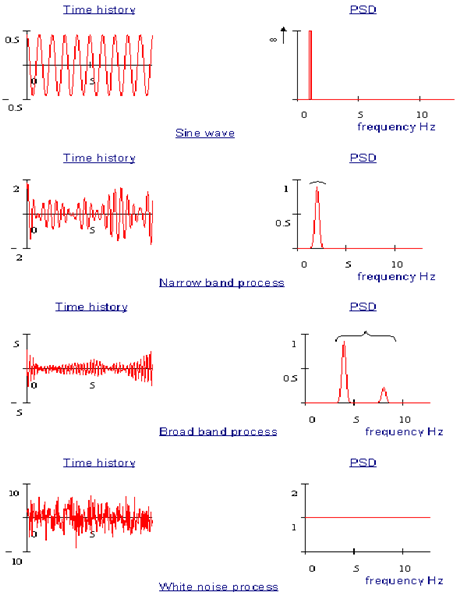
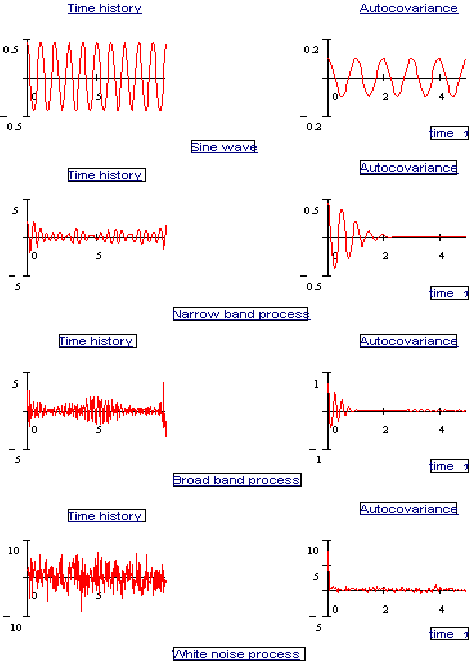
Figure 8‑47 shows four types of process. The distinction between narrow and broad banded processes becomes much more apparent from the PSD plots than the time histories.
Figure 8‑47 Time Histories and Corresponding PSDs
Time Signal Regeneration from PSDs
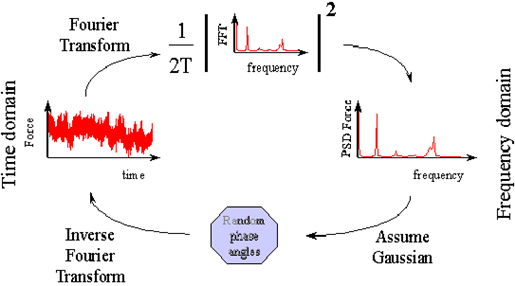
Earlier it was shown how a time history may be expressed in either the time or frequency domains. Transformation from one domain to the other is carried out using the Fourier transform pair. PSDs express the statistics of a random process in the frequency domain and in many instances it is desirable to obtain a time history from a PSD. PSDs are given in many of the design standards where random loading is involved. If the designer wishes to determine how a non-linear structure will react to a typical random load history it is necessary to regenerate a characteristic time history from the design PSD, this can then be analyzed using a dynamic analysis program in the time domain. For linear structures this step is not necessary as the dynamic analysis may be carried out entirely in the frequency domain. This text deals with linear analysis however it is still beneficial to describe the process of time signal regeneration from PSDs.
Unlike the Fourier density spectra the PSD does not contain information about the phase relationships between the sinusoidal waves that make up the time history. It does however, contain information on the Mean square amplitude of each wave. In order to regenerate a time history it is necessary to reintroduce the phase relationships between each of the waves. For many signals it has been found that the phase relationships follow a uniform random distribution between 0 and
and with this knowledge it is therefore possible to regenerate a time history. Time histories obeying this trend are said to be 'Gaussian Random' processes. The regenerated time history will not be the same as the original measured time history since the phase angles are now different. It is still statistically characteristic though. There are a number of methods used for time history regeneration, this text looks at the most intuitive method of evaluating the random phase angles and taking the inverse Fourier transformation.
The time history is formed by the summation of a number of sinusoidal waves of differing frequency, amplitude and phase. The n
th wave may be expressed in the form given in
(8‑21) where
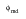
is the random phase angle between 0 and
radians.
(8‑21)

Using the complex relationships given in
(8‑3) and
(8‑4), the double sided PSD and random phase angle can be expressed in complex form as
(8‑22).
(8‑22)

Solving these two simultaneous equations yields values for the Fourier coefficients A
n and B
n defined in
(8‑4). Using the normalization described earlier the complex Fourier density function can be determined. Having obtained the Fourier density function the time history regeneration can be accomplished by taking the inverse Fourier transform. The formulation is given in
(8‑23).
.

and
(8‑23)
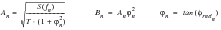
The method proves difficult to implement computationally however because large numeric precision errors occur when taking the tangent of a random number between 0 and
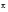
. This is not a serious problem in the context of this thesis but should be considered for other applications where time history regeneration is required.
(8‑24) gives the formulation for regenerating a time history from a single sided PSD.
and
(8‑24)
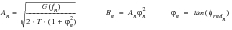
Summary of Fourier Transformation and PSDs
Figure 8‑48 illustrates the transformation between the time and frequency domains. The frequency domain is another way of representing a time history. Transformation between the time and frequency domains is accomplished using the Fourier Transform Pair. There are two forms of transform, the integral and the discrete transform. The discrete transform is particularly useful for transforming digitally measured time histories such as those recorded using data acquisition. The “Fast Fourier Transform” is now universally used for this purpose.
Figure 8‑48 The Fourier Transform Between Time and Frequency Domains
The Fourier transform gives a Fourier Density Spectrum. This is complex and may be single or double sided. Single sided spectra are a special case of the double sided spectra where the negative frequencies are the complex conjugate of the positive frequencies. This condition arises when the time history is Real. All measured time histories are real and are usually expressed as single sided spectra.
It is often more convenient to deal with the statistics of a random process than either a time or frequency domain representation of the actual signal. For this reason the Power Spectral Density (PSD) is used. The PSD represents the Mean Square amplitude of the sinusoidal waves that comprise the time history. It is often necessary to regenerate a statistically representative time history from a PSD, the PSD does not contain information on the phase relationships between the sinusoidal waves and this therefore needs adding. Provided the process is 'Gaussian Random' then the phase relationships will follow a uniform random distribution.
Figure 8‑49 illustrates the transformation between the time domain and the PSD.
Figure 8‑49 Transformation Between Time History and PSD
What Does the FFT Tell Us?
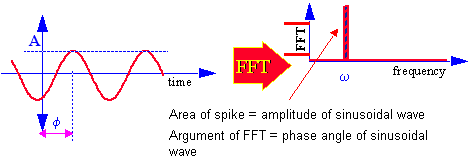
The figure below shows a physical representation of what the frequency domain graphs are showing.
The FFT is a complex number given with respect to frequency. A sine wave of frequency ω, amplitude A and initial phase angle φ is represented in the frequency domain by a spike occurring at ω along the frequency axis. If the magnitude of the complex FFT is plotted, then the area under the spike is found to be the amplitude A of the sine wave. When the argument of the complex FFT is plotted then the area is found to be initial phase angle φ of the sine wave.
The frequency, amplitude and phase of the sine wave is therefore retained in both the time and frequency domains. As it is rather cumbersome to plot complex numbers, we generally plot two separate graphs; one for the amplitude and the other for the phase angle.
How Do We Use FFTs?
The French Mathematician J. Fourier (1768-1830) postulated that any periodic function can be expressed as the summation of a number of sinusoidal waves of varying frequency, amplitude and phase. Each individual sinusoidal wave can be expressed as a spike in the frequency domain and as the number of sine waves increase, the difference in frequencies between them tend to zero and so the spikes tend to merge into a continuous function. Therefore, if we want to find the amplitude and phase of the sinusoidal waves in a particular frequency range, say between 2 and 2.5 Hz, we can measure the area under the curve in that frequency range. As this area is given as a complex number, the amplitude content can be obtained by taking the modulus of this and the phase content from the argument.
For many engineering cases we are only interested in the amplitude of the various sine waves and are not concerned with the initial phases. In fact, in many cases we find that the initial phase angle is totally random, and so it proves unnecessary to show it. For this reason the Amplitude Spectral Density (ASD) function alone is usually shown. This is simply a plot of the modulus of the complex FFT given with respect to frequency.
Response of a Linear System to a Single Random Process
The work carried out so far has enabled us to represent a measured time history in the frequency domain in the form of a PSD. This measured time history may be that of wind speed measured using anemometers or stresses in a structural component measured using strain gauges. In the case of a wind turbine, for example, the PSD is likely to be given for the turbulent wind speed witnessed near the ground. It is important to understand how a structure will react to the dynamic wind loading. We could take the PSD and regenerate a statistically representative time history and then analyze this using a dynamic analysis program in the time domain but this is very time consuming as the analysis process is complicated. For structures which behave in a linear way the analysis may be done more efficiently in the frequency domain.
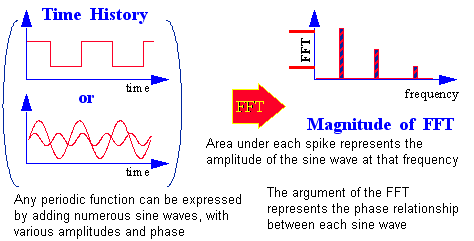
A linear system is one where the output is related to the input by a linear transfer function. In the case of a wind turbine blade the load on the turbine blade could therefore be expressed as
(8‑25).
e.g., the aerodynamic force on a turbine blade is given as the product of the wind speed v(t) and the linear aerodynamic transfer function g.
(8‑25)
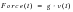
If the wind speed is expressed in terms of the Fourier density function then the aerodynamic force will then be given in the frequency domain using
(8‑26).
(8‑26)
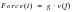
It is convenient to obtain the response as a PSD S
F(f). From
(8‑18), the double sided PSD of force can be expressed as
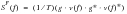
. If the wind speed is also expressed as a double sided PSD S
v(f) then the PSD of force is given by a linear transfer function in the frequency domain as in
(8‑27).
(8‑27)
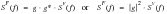
This relationship also holds between single sided PSDs as expressed in
(8‑28).
(8‑28)
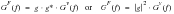
Dealing With Multiple, Partially Correlated Random processes
The previous section describes the transformation of random time histories into the frequency domain using the Fourier transform pair. A simple relationship can be used to generate the Power Spectral Density function (PSD) which contains statistical properties of the random time history. We shall now look at an alternative method for generating PSDs. The method uses a statistical property of the time history, namely the Autocovariance function, as a method of obtaining the PSD. Although the Fourier transform is now universally used for obtaining PSDs, the method discussed here is important in understanding the concept of random processes. We shall expand on this theory to also include multiple random events, and will define the cross-power spectral density function to represent the statistical relationships between two random events.
Definition of the Autocovariance Function
The Autocovariance function is a statistical property that describes the frequency or periodic properties of a time history. The autocovariance function is defined in
(8‑29) where E{} is the expectation operator defined by
(8‑29)
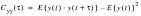
The notation C
yy indicates the autocovariance function for a single process y. The notation is introduced at this stage to distinguish between the 'cross-covariance function (C
xy)' for two random processes x and y, this is discussed in this text. For all analysis carried out in this thesis random processes are assumed stationary and have a zero mean.
(8‑29) can therefore be rewritten as the infinite time average given by
(8‑30), the Autocovariance function.
(8‑30)
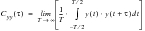
The autocovariance function is plotted for a number of time histories in
Figure 8‑50. For periodic processes with period T, the autocovariance function is also periodic with the same period. For stationary processes the autocovariance function is even, i.e. C
yy(
)=C
yy(-
), and may be expresses as a single sided function. As stationarity is assumed for all random processes throughout this text the single sided autocovariance function is used.
Note: | For t = 0, the autocovariance tends to the variance of the time history. |
Figure 8‑50 Time Histories and Corresponding Autocovariance's
A sinusoidal time history appears as a single spike on the PSD plot. The spike is centered at the frequency of the sine wave and the area of the spike represents the mean square amplitude of the wave. In theory this spike should be infinitely tall and infinity narrow for a pure sine wave, however because of the numerical analysis the spike will have a finite width and will therefore have a finite height. Remember, with PSD plots we are interested in the area under the graph and not the height of the graph.
A narrow band process is one which is built up of sine waves covering only a narrow range of frequencies. A narrow band process is typically recognized in the time history by the amplitude modulation, often referred to as a beat envelope.
Wide band processes are built up of sine waves over a broad range of frequencies. These are shown in the PSD plot as either a number of separate spikes or one wide peak covering many frequencies. This type of process is usually more difficult to identify from the time history but is typically characterized by its positive valleys and negative peaks.
White noise is a a special time history which is built up of sine waves over the whole frequency range.
Transformation Between Autocovariance and PSD
In this section it is shown that the Fourier transform pair can be used to transform between the autocovariance function and the PSD. In this sense the autocovariance function is similar to a time history representation of the PSD. In effect it is the time history of the mean square amplitude of the sinusoidal waves with a zero phase angle.
The autocovariance function for a zero mean, stationary random process is defined in
(8‑30). From
(8‑12) the term y(t+

) may be expressed in terms of the Fourier transform pair as
(8‑31).
(8‑31)

Substituting this into
(8‑30) and simplifying yields
(8‑32).
(8‑32)
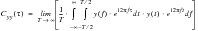
Now from
(8‑12) we know that
therefore, the autocovariance function may be expressed as
(8‑33).
(8‑33)
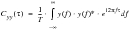
It is now possible to recognize the similarity with
(8‑18) used to transfer from the Fourier density function to the PSD. Using this relationship the autocovariance function may be expressed in terms of the PSD as
(8‑34), i.e. the inverse Fourier transform of the PSD S
yy(f)
(8‑34)
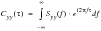
The transformation between the autocovariance function and the PSD can therefore be accomplished using the Fourier transform pair as shown in
(8‑35).
(8‑35)
| The inverse Fourier transform |
| The Fourier transform |
The notation Syy is adopted here to describe the Auto-power spectral density function as opposed to the cross-power spectral density function (Sxy) between two random processes x and y, we will look at this next.
Multiple Random Processes: The Principle of Cross-covariance
To this point we have considered the analysis of one random process, this section introduces the analysis of multiple random processes.
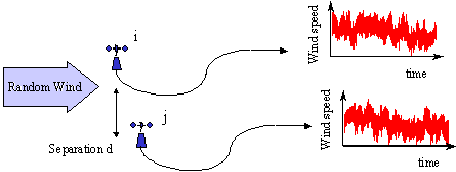
Figure 8‑51 shows two anemometers measuring wind speed placed side by side with separation d. From each anemometer a time history of the wind speed is produced. PSDs can be calculated from these and provided that the wind field is homogeneous, both PSDs will be the same. From this it is concluded that the mean square amplitudes of the sinusoidal waves which comprise the time histories are the same. The PSDs however give no information about the phase relationships between the two measured time histories.
In this section we are interested in the sequential relationship between the two time histories. If the two anemometers are far enough apart then the wind speed witnessed by one will be completely independent of the other, they are said to be uncorrelated. As they are moved closer together then a correlation between the two time histories will be noted. Correlation occurs because the random turbulent wind incident on anemometer x is sufficiently large to also be influencing anemometer y.
Figure 8‑51 Multiple Random Processes
The covariance function may be used to find the sequential relationships between the two time histories in the same way as before. In this case
(8‑29) is written as
(8‑36). This is known as the Cross-covariance function. In this case we now compare time histories x and y.
(8‑36)
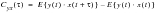
The notation C
yx is used to describe the Cross-covariance function between the two random processes x and y. It effectively tells us what the effect on y would be should a random process hit x. Assuming that the random processes are stationary and have a zero mean then the cross-covariance function may be transformed to a PSD using the Fourier transform. The resulting PSD S
yx is now termed the 'Cross-power Spectral Density Function'. This relationship is expressed in
(8‑37).
(8‑37)
| The cross-covariance function between processes x and y. |
| The cross-power spectral density function between processes x and y. |
Normalized Covariance and Time Scales
It is often convenient to normalize the covariance function in order to compare different time histories with different scales of measurement. This is achieved by dividing the covariance by the variance. The normalized covariance function is defined by
(8‑38), it has the same shape as the covariance function except that the ordinate is scaled to have a value of 1 for
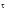
=0.
(8‑38)
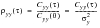
The time scale is defined as the area under the normalized covariance function as
(8‑39). For a random time history this roughly equates to the mean zero crossing period of the time history. For a periodic time history this is not the case however as
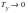
.
(8‑39)
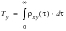
The Coherence Function
Another way of representing the correlation between two random processes is through the coherence function. The coherence represents the degree of correlation between two random processes. Two uncorrelated events show zero coherence where as two fully correlated events show unit coherence. The coherence function is defined in
(8‑40) as a ratio of the cross-power spectral density function to the geometric mean of the two auto-power spectral density functions.
(8‑40)
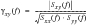
Many design standards quote the auto-power spectral density function which the designer should use to verify the design. Where there are correlated multiple events it is often easier to express the correlation in terms of the coherence function than to specify many cross-power spectral density functions separately. The designer may then derive his own cross-spectral density functions by rearranging
(8‑40). For certain analyses, such as wind turbulence, the coherence function is expressed as a function of frequency and separation distance.
Response of a Linear System to Multiple, Partially Correlated Random Loads
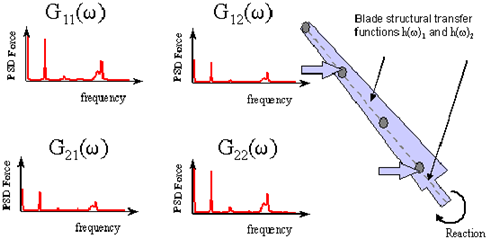
Figure 8‑52 illustrates the loading on a wind turbine blade due to two random processes. In order to calculate the reaction to this loading, it is insufficient to simply sum the reactions from the two PSDs. Instead, we must sum the reactions from the PSDs and cross-PSDs. The cross power spectra contain information on the joint statistics of the two processes. If the two processes are correlated then the sequencing effect of the two processes may act to either increase or decrease the overall loading on the blade. A very good mathematical explanation of this can be found in Newland (Ref. 105.).
Figure 8‑52 Reaction to Multiple Random Loading
The total reaction force on the blade can be found in the time domain from
(8‑41).
(8‑41)
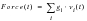
If the wind speed is expressed in terms of the Fourier density function then the aerodynamic force will then be given in the frequency domain using
(8‑42).
(8‑42)
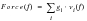
It is convenient to obtain the response as a PSD S
F(f). From
(8‑18) the double sided PSD of force can be expressed as
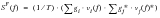
. If the wind speed is also expressed as a double sided PSD, S
v(f), then the PSD of force is given by
(8‑43).
(8‑43)
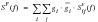
This relationship also holds between single sided PSDs as expressed in
(8‑44).
(8‑44)
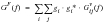
Matrix Form of the Cross-power Spectral Density Function
The Auto- and cross-power spectral density functions may be expressed in matrix form, this permits the rapid calculation of responses using matrix algebra. The auto-power spectral values are located along the leading diagonal while the cross-power terms are located in the remaining cells as illustrated in
Figure 8‑53.
Figure 8‑53 Cross-power Spectral Density Matrix
Using matrix algebra,
(8‑44) may be expressed as
(8‑45).
(8‑45)
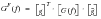
Where [G(f)] is the cross-power matrix and [g] is a vector of gain factors.
Time Domain Characterization of Fatigue Life Estimation
With MFLF a traditional S-N curve as shown in
Figure 8‑54 is used to model the material properties of the components being analyses.
Figure 8‑54 S-N Relationship - an Experimental Law for Constant Amplitude Loading
This figure simply shows that, under constant amplitude cyclic loading, a linear relationship exists between cycles to failure N and applied stress range S when plotted on log-log paper.
This is an alternative form of the S-N curve to that used for the rest of the MSC Fatigue tools (see appendix 2) where,
(8‑46)
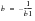
(8‑47)

Because real signals rarely conform to this ideal constant amplitude situation, an empirical approach is used for calculating the damage caused by stress signals of variable amplitude. Despite its limitations, Miner's rule is generally used for this purpose as shown in
Figure 8‑55.
The relationship between the form of S-N curve used for MFLF (material constants b and k) and the convention used for the rest of MSC Fatigue tools (material constants b1 and SRI1):
(8‑48) MFLF N.Sb = K
(8‑49) FEFAT N-b1.S = SRI1
i.e. log N + b.log S = log K
The above two equations are valid for all N and S, therefore
(8‑50)
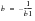
(8‑51)
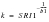
and
(8‑52)
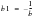
(8‑53)SRI1=K-b
An example...
b1 = -0.102
SRI1 = 1868 MPa
b=9.8
K= 1.147 x 1032 (MPa9.8)
Figure 8‑55 Palmgren-Miner Cumulative Damage Hypothesis -
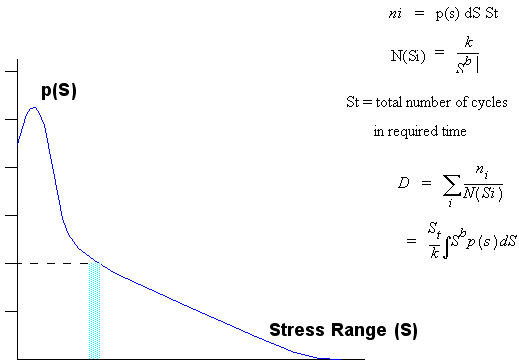
Linear Damage Rule and Probability Density Functions (PDFs)
Percentage of damage (Damage Ratio)
(8‑54)
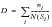
ni= actual counted number of cycles
N(Si)=allowable (from S-N plot) number of cycles
The linear relationship in
Figure 8‑55 assumes that the damage caused by parts of a stress signal with a particular range can be calculated and accumulated to the total damage separately from that caused by other amplitudes. A ratio is calculated for each stress range, equal to the number of actual cycles at a particular stress range n divided by the allowable number of cycles to failure at that stress N (obtained from the S-N curve). Failure is assumed to occur when the sum of these ratios, for all stress ranges, equals 1.0.
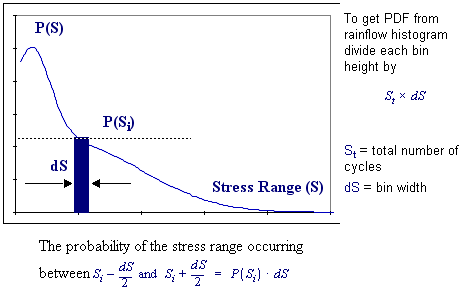
If n is obtained from a time history of stress, then the most convenient way of storing the information is in the form of a probability density function (PDF) of stress ranges. A typical representation of this function is the diagram in
Figure 8‑55.
Since
rainflow ranges of stress are generally regarded to give the best indication of the fatigue damaging potential of a random signal, it is the PDF of rainflow ranges which is the desired result. Rainflow ranges have been widely used for estimating fatigue damage from random signals since Matsuishi and Endo first introduced the concept to the scientific community over twenty years ago (Ref. 77.). When the loading sequence is specified as a time history, the procedure for calculating rainflow ranges is relatively simple. An example of the way rainflow ranges are extracted from a time signal is given in
Figure 8‑56. For the potential of a random signal, it is the PDF of rainflow ranges which is the desired result. Rainflow ranges have been widely used for estimating fatigue damage from random signals since Matsuishi and Endo first introduced the concept to the scientific community over twenty years ago. When the loading sequence is specified as a time history, the procedure for calculating rainflow ranges is relatively simple.
Figure 8‑56 Rainflow Cycle Counting
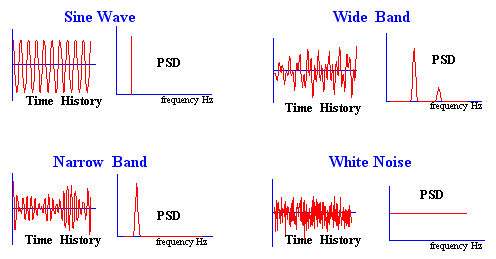
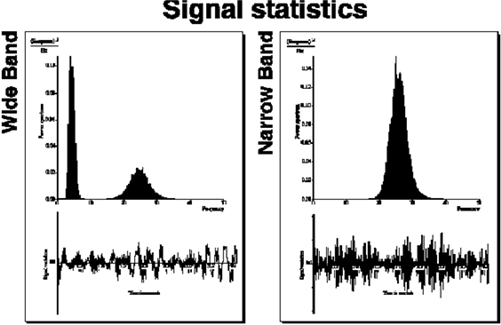
An important characteristic of any time signal is related to its frequency content.
Figure 8‑57 shows two different types of structural response. In each case both the time series and its corresponding PSD are shown. The right hand response contains predominantly one frequency as indicated by its PSD. The corresponding time signal shows a classical
narrow band response, i.e., constant frequency, slowly varying envelope. The structural response on the left contains a spread of frequencies, as indicated by its PSD. This can also be identified in its corresponding time series. This type of response is termed
wide band. If the PSD has a flat top extending (theoretically) to infinity (as is the case with so-called white noise or shot noise) then the process is often referred to as
broad band.
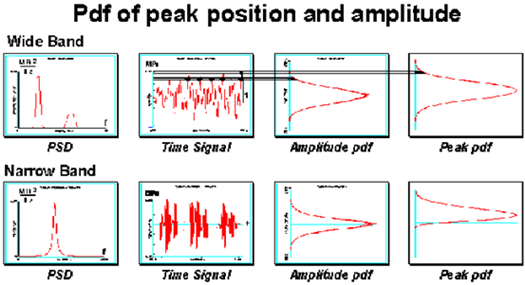
An important distinction between these two types of responses, in terms of their fatigue damaging content, can be determined by considering the form of peak pdf’s shown in
Figure 8‑58. Most importantly, for the narrow band signal virtually all peaks occur above the mean level. Because of this, and the fact that the envelope is slowly varying, the PDF of peak position is identical to that of (half) cycle ranges. Also, because of the slowly varying envelope these cycle ranges are also rainflow ranges.
Figure 8‑57 Signal Statistics
Figure 8‑58 Pdf of Peak Position and Amplitude
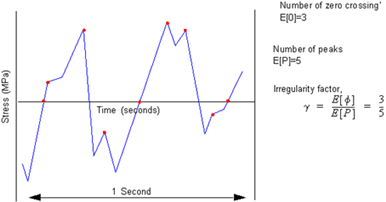
A numerical indication of this characteristic can be determined from the number of so-called
zero crossings and
peaks in the signal.
Figure 8‑59 shows a section cut out from a typical wide band signal. E[0] represents the number of (upward) zero crossings, or mean level crossings for a signal with a non-zero mean. E[P] represents the number of peaks in the same sample. These are both normally specified for a typical one second sample. The
irregularity factor (
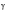
) represents the number of zeros divided by the number of peaks. This is discussed further in the next section.
Figure 8‑59 Expected Zeros, Peaks, and Irregularity Factor
Characterization of Structural Response in the Frequency Domain
Since we are concerned with structural systems analyzed in the frequency domain, we require a method for extracting the PDF of rainflow ranges directly from the PSD of stress. The characteristics of the PSD which are used to obtain this information are the nth moments of the PSD function: as shown in
Figure 8‑60 below.
Figure 8‑60 Moments from a PSD
Some very important statistical parameters can be computed from these moments such as the expected number of zeros and peaks per second. From these the irregularity factor,
, can be computed which, as described earlier, gives an indication of the spread of frequencies present in the signal: This is illustrated in the equations below.
(8‑55)
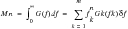
(8‑56)

(8‑57)
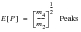
(8‑58)
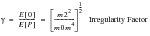
The value of
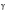
varies between 1.0 and 0.0. A value of 1.0 corresponds to a narrow band signal which, as the term implies, means that the signal contains only one predominant frequency. A value of 0.0 implies that the signal contains an equal amount of energy at all frequencies.
Probability Density Functions (PDFs)
The most convenient way, mathematically, of storing stress range histogram information is in the form of a probability density function (PDF) of stress ranges. A typical representation of this function is shown below. It is very easy to transform from a stress range histogram to a PDF, or back. The bin widths used, and the total number of cycles recorded in the histogram are the only additional pieces of information required.
Fatigue Damage for Random Response Histories
Once the stress range histogram has been converted into a stress range PDF then there is an elegant and efficient equation to describe the expected fatigue damage caused by this loading history. The probability density function P(S) simply represents the characteristics of the loading. In order to compute fatigue damage over the lifetime of the structure (T) the form of material (S-N) data must also be defined using the parameters k and m. In addition, the total number of cycles in time T must be determined from the number of peaks per second E[P]. If the damage caused in the time T is greater than 1.0 then the structure is assumed to have failed. Or alternatively, the fatigue life can be obtained by setting T = 1.0 and then finding the fatigue life in seconds from the equation.
Frequency Domain Approaches of Life Estimation
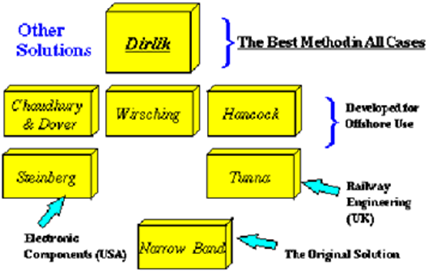
Narrow Band
The first frequency domain method for predicting fatigue damage from PSD's made use of the so-called narrow band approach (Ref. 77.) mentioned above, which assumes that the PDF of peaks is equal to the PDF of stress amplitudes. The narrow band solution was then obtained by substituting a function of the Rayleigh PDF of peaks for the PDF of stress ranges. The problem with this solution is that by using the Rayleigh PDF, positive troughs and negative peaks are ignored and all positive peaks are matched with corresponding troughs of similar magnitude regardless of whether they actually form stress cycles. For wide band response data the method therefore overestimates the probability of large stress ranges and so any damage calculated will tend to be conservative. The narrow band formula is illustrated here.
The total number of cycles is given by E[P].T in this formula. Expected damage:
(8‑59)
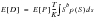
where s=stress range.
Expected damage:
(8‑60)
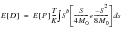
Note: | E[P].T = total number of cycles in time T = St as used earlier |
Many expressions have been proposed to correct this conservatism. Most were developed with reference to offshore platform design where interest in the techniques has existed for many years. In general, they were produced by generating sample time histories from PSD's using Inverse Fourier Transform techniques, from which a conventional rainflow cycle count was then obtained. The solutions of Wirsching (Ref. 78.), Chaudhury and Dover (Ref. 79.), and Hancock (Ref. 80.) were all derived using this approach.
Wirsching's Equation:
(8‑61)
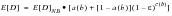
a(b)=0.926-0.033b; c(b)=1.587b-2.323;
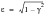
is called the bandwidth parameter which is an alternative version of the irregularity factor.
Hancock's Equation
(8‑62)
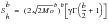
This solution is given in the form of an equivalent stress range parameter Sh, where;
(8‑63)

Chaudhury and Dover Equation
Their equation was derived using a similar approach and is given in (Ref. 79.):
The fatigue damage can then easily be obtained by substituting this into the general damage equation used when deriving the narrow band solution;
(8‑64)
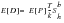
Tunna Equation
He (Ref. 96.) (Ref. 97.) proposed a different formulation using a revised form of the Rayleigh PDF for stress ranges as follows:
(8‑65)

For
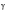
= 1.0 this formula becomes the narrow band formula given earlier.
Steinberg’s Three-band Technique:
As a rough estimation for the fatigue damage, Steinberg proposed a three-band technique (Ref. 98.). The basis for this method is the Gaussian distribution. The instantaneous stresses (or accelerations) between +1
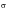
(
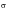
is the root mean square) and -1
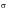
are assumed to act at the 1
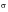
level 68.3% of the time. The instantaneous stresses (or accelerations) between +2
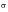
and -2
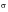
are assumed to act at the 2

level of 95.4-68.3, or 27.1% of the time. The instantaneous stresses (or accelerations) between +3

and -3
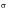
are assumed to act at the 3

level 99.-95.4, or 4.33% of the time. These values are shown below for the 3 bands:
• 1
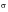
values occur 68.3% of the time
• 2
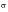
values occur 27.1% of the time
• 3
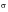
values occur 4.33% of the time
The fatigue damage is thus estimated based on these three stress levels.
The approach of Steinberg leads to a very simple solution based on the assumption that no stress cycles occur with ranges greater than 6 rms values. The distribution of stress ranges is then arbitrarily specified to follow a Gaussian distribution. This defines the stress range cycles to occur with the following probability.
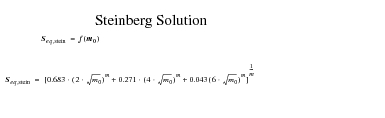
It is possible to define the maximum stress range used in the subsequent fatigue analysis. If this is set at 6 rms it is possible to see that large stress ranges are omitted using this approach. MSC Fatigue will set this value automatically, if not over ridden, to be somewhere around 9 rms for stress range! Anything less than this is likely to result in an under prediction of fatigue damage. Of course this is counter balanced by the fact that medium range stress cycles of levels between 4 and 6 rms are over predicted. Nevertheless it must be stated that this approach is very questionable. It is included only as a means of allowing designers in the electronics industry, who are used to the Steinberg approach, a means of comparison.
Dirlik’s Empirical Formulation
Since these solutions assume that the PDF of rainflow ranges is the factor which controls fatigue life, a better approach is to estimate this directly from the PSD without using the narrow band approach as a starting point. Both empirical and theoretical expressions have been produced in this way. They are generally only applicable to the offshore loading conditions for which they were developed.
Dirlik (Ref. 81.) has produced an empirical closed form expression for the PDF of rainflow ranges, which was obtained using extensive computer simulations to model the signals using the Monte Carlo technique. Dirlik's solution is illustrated in the equations below:
(8‑66)
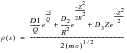
(8‑67)
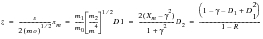
(8‑68)
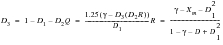
Dirlik's empirical formula for the PDF of rainflow ranges has been shown to be far superior, in terms of accuracy, than the previously available correction factors. However, the need for certification of the technique before its use meant that theoretical verification was required. This was achieved in 1988 (Ref. 82.) when a theoretical solution for predicting rainflow ranges from the moments of the PSD was produced. A detailed description of this method is given in (Ref. 84.).
An essential requirement of any theoretical solution was a statistical rather than spatial description of rainflow ranges. This was initiated in (Ref. 83.) and further extended later (Ref. 84.) to the form shown in
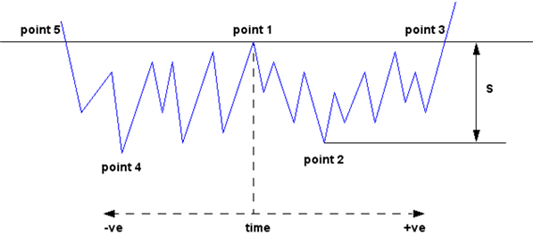
Figure 8‑61. The horizontal axis represents time and the vertical axis, stress range. -ve and +ve time is indicative of past and future events.
All the above methods are included in MSC Fatigue; this is because certain industries have developed design standards which assume that a particular approach will be used. Unless you are restricted by the requirements of a standard, we would always recommend that you use the Dirlik analysis as this generally proves the best approach for all applications.
Rainflow Range Definition
Figure 8‑61 A New Rainflow Range Definition
In practical terms this definition asserts that the probability of three events U1, U2, and U3 can be used to define the probability of a rainflow range S occurring with a peak at the level corresponding to point 1 and a trough at a level corresponding to point 2.
Obviously there are a number of configurations that can occur with the same distance or range between point 1 and point 2 as shown in
Figure 8‑61. The total probability of a particular rainflow range is therefore the summation of these individual probabilities. The definition is expressed in terms of peak and trough values and the relationships between these. This is not surprising since fatigue damage is determined by ranges of stress, which are themselves determined by peak and trough values.
The problem then reduces to one of finding the individual probabilities (for each value of ip) of U1, U2, and U3 and can be solved using the Markov chain model.
In order to reduce the computational effort required to obtain a solution, the assumptions of normality and stationarity were used. By assuming that the signal is stationary, one can assume that the signal is statistically equivalent after reflection about a vertical axis. U1 and U2 can then be treated in the same way. By assuming the signal is Gaussian, one can assume that the signal is statistically equivalent after reflection about a horizontal axis. Event U3 can then be treated in the same way as events U1 and U2.
The task of obtaining these three events then reduces into that of obtaining the long run absorption probabilities of transitions into states 1 and 2. These are:
• Given the assumption that a signal starts from some peak at level ip, what is the probability that it will move (via any number of peaks and troughs) to some other level kp directly, without going back to (or above) the level of ip (the first peak) or to a level below kp. Level kp is termed state 1.
• Given the assumption that a signal starts from some peak at level ip, what is the probability that it will move (via any number of peaks and troughs) to some other level below kp, without going back to (or above) the level of ip or into the level of kp. This level below kp is termed state 2.
Of course this information must be evaluated for every configuration of peak and trough in the signal.
If the Markov assumption is valid, that the probability of going to any adjacent peak (or trough) in the signal is dependent only on the position of the current trough (or peak), then the probabilities of the above multi-transition events can be obtained from the one step peak-to-trough and trough-to-peak probabilities using Markov Chain theory. This assumption is generally true for typical engineering situations.
The one step transition probabilities are obtained using the (approximate) solution of Kowalewski (Ref. 85.) for the PDF of adjacent peaks and troughs in a Gaussian signal. The reader is referred to (Ref. 85.) for a detailed description of the method of evaluating the Markov Chain model.
This solution is more complicated to evaluate computationally than Dirlik’s expression which was given earlier. Furthermore, Dirlik’s expression has been shown (see (Ref. 88.)) to be at least as accurate. For these reasons it is not included in the MFLF and FEVIB programs. It is presented here only to provide the theoretical background required for certification bodies to approve the overall approach.
All of the frequency domain techniques described in this note require the process being analyzed to be stationery, Gaussian and random. In theory this can be a very onerous requirement but in practice a considerable divergence from rigorous compliance can be tolerated.
Vibration Analysis using Finite Elements
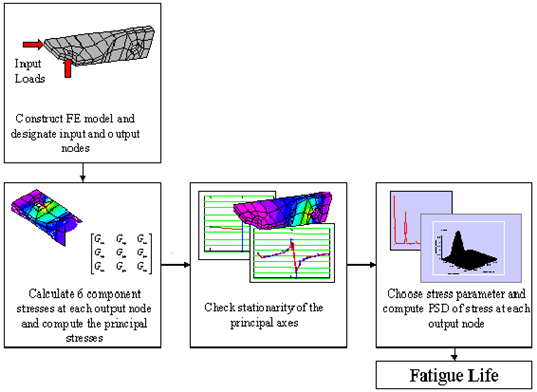
In the previous section we discussed how fatigue life is determined from a PSD of stress. What is required now is a finite element analysis capable of evaluating such PSDs for each node in a structural component. The analysis described in this section requires the following:
1. A finite element model of the component.
2. A list of nodes to which input loads are applied.
3. Autopower and cross-power spectral density functions (PSDs & CPSDs) of the actual input loads.
4. A list of output nodes over which to calculate the fatigue damage.
An overview of the analysis procedure is given in
Figure 8‑62.
Figure 8‑62 Overview of the Analysis Process
The theories employed are best described by example. We will start with a simple one-degree of freedom system subjected to a single random input load, the concept of a linear transfer function is introduced in this example. For the second example we consider the case of a two degree of freedom system subjected to two partially correlated random loads, the matrix form of the transfer equation and cross-power spectra is introduced here. Finally, we consider the case of a multiple degree of freedom system subjected to multiple partially correlated random loads giving six component stresses at the node under investigation. In this example we look at resolving the component stresses into a single effective stress PSD (e.g. maximum principal, von Mises, etc.), and also consider the problem of multiaxiality and discuss how to detect this.
One Degree of Freedom System with One Random Load
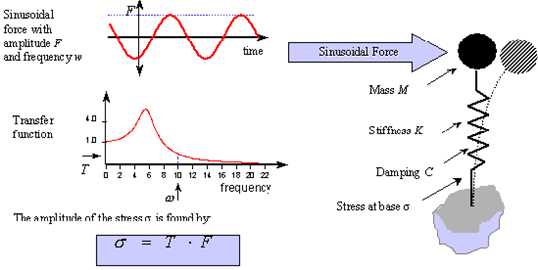
If a sinusoidally varying force is applied to a linear structure then the structure will respond with a sinusoidally varying stress of the same frequency as the applied load, this is illustrated in
Figure 8‑63.
Figure 8‑63 The Concept of a Linear Transfer Function
For a linear structure we expect that an increase in the amplitude of the forcing function will cause a proportional increase in the stress. This leads to the concept of a response parameter relating the amplitude of stress to the amplitude of the forcing function.
The amplitude of the stress varies with respect to the frequency of the applied load and so the response parameters are frequency dependent. The Transfer Function is defined as a plot of the response parameters with respect to frequency as shown in
Figure 8‑63. We can therefore use the transfer function to predict the amplitude stress of the structure by multiplying the amplitude of the load F by the Transfer Function T for a particular frequency of applied load.
The transfer function can also be used in the frequency domain to relate input load PSDs to output stress PSDs, this is discussed in
An Introduction to Random Process Theory, 680 and is given in
(8‑69).
(8‑69)
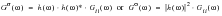
Where
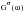
is the PSD of stress, G
ii(
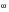
) is the PSD of input stress, h(
) is the linear transfer function and h(
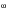
)* is the complex conjugate of h(
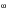
).
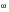
is the frequency expressed in circular measure (rad/sec).
For a single degree of freedom system the linear transfer function is easily obtained using
(8‑70).
(8‑70)
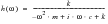
Where, m is the nodal mass, c is the element damping and k is the element stiffness.
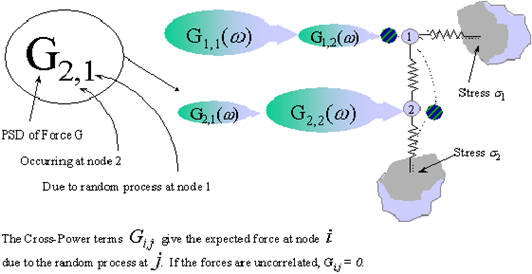
Two Degree of Freedom System with 2 Partially Correlated Random Loads
Figure 8‑64 Two Degree of Freedom System, Partially Correlated Random Loads
Each random load is described by its Auto-power spectral density function (PSD). If both random loads are partially correlated we must also include cross-power spectral density functions (CPSD) to adequately model the sequential effects between the two processes. The PSD of stress witnessed at the base of the structure was derived earlier and is given by
(8‑71).
(8‑71)
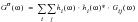
Where
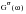
is the PSD of stress, G
11(
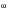
) and G
22(

) are the autopower spectra of inputs 1 and 2 respectively, and G
12(
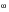
) and G
21(
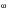
) are the cross power spectral density function between inputs 1 and 2. h
1(
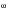
) and h
2(
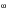
) are the transfer functions between stress and load input at nodes 1 and 2 respectively.
To improve computational efficiency and simplify the arithmetic, it is desirable to express
(8‑71) in matrix form as
(8‑72).
(8‑72)
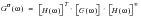
Where
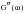
is the PSD of stress, [H(
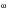
)] is a vector of transfer functions defined as
[H(w)]* is the complex conjugate of [H(
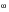
)] and [H(
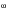
)]
T is the transpose. [G(
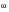
)] is a symmetric, square matrix of auto- and cross-power spectral densities of loading, the auto-power terms lying along the leading diagonal.
Multiple Degree of Freedom Systems
We deal with multiple degree of freedom structures in exactly the same way as single degree of freedom structures, however, the FE analysis now yields a transfer function in terms of six component stresses at the output node. This is illustrated in
Figure 8‑65.
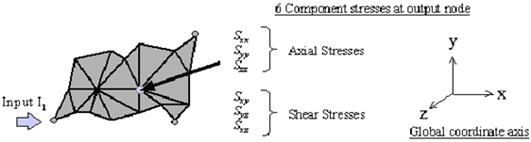
Figure 8‑65 Transfer Function Calculated as Six Component Stresses
The finite element solver returns six component stresses at each output node in response to a single input load, these being three axial stresses and three shear stresses along the global coordinate or the element coordinate axis. We require a single stress result for use in the transfer function, this can either be the maximum principal or an effective stress parameter based on some yield criterion such as Tresca or von Mises.
The three principal stresses can be determined from the six components using matrix routines for determining eigenvalues and eigenvectors. The components are expressed in matrix form, as shown in
(8‑73). The eigenvalues yield the principal stresses while the eigenvectors yield the directional cosines of the principal axes.
(8‑73)
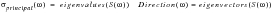
Where
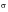 principal
principal(
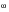
) is a vector of the three principal stresses, Direction(
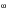
) is a matrix of the direction cosines for the three principal axes normalized to yield three unit column vectors, the n
th column referring to the n
th eigenvalue. S(
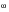
) is a 3 x 3 matrix of the component stresses defined as
The eigenvalues and eigenvectors are complex retaining both the amplitude and phase information of the transfer function. It is desirable to combine these two matrices to form a single tensor matrix with three columns each representing the vector of a particular principal stress. The magnitude of each vector will now represent the magnitude of the principal stress. As the eigenvector matrix is a unit matrix, we can evaluate the new stress tensor matrix s as
(8‑74).
(8‑74)
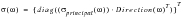
Where diag(
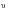
) is a function to return a diagonal matrix of the vector
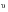
.
The single stress parameter can now be determined depending on the user’s choice.
Maximum principal stress | |
von Mises stress | |
Tresca effective stress | |
Note: | The three stress parameters above are real, it is no longer necessary to retain the complex notation as phase is not required. |
The Case of Multiaxiality
In other parts of this guide we talk about multiaxiality (or biaxiality) and categorize structures as uniaxial, proportional biaxial, and non-proportional biaxial. In terms of the principal stress tensor these three cases directly relate to the following descriptions:
1. Uniaxial - One principal stress is much larger than the other two, which tend to zero. The stress tensor is stationary and doesn't rotate.
2. Proportional, multiaxial - Two or three principals are greater than zero but increase and decrease proportionally. Again the stress tensor doesn't rotate.
3. Non-proportional, multiaxial - Two or three principals are greater than zero and increase and decrease disproportionately to each other. The stress tensor is seen to rotate.
The first two cases can be dealt with using the maximum principal or a von Mises stress invariant, in these cases we notice that the direction of the stress tensor is stationary and the fatigue crack will propagate in a relatively constant direction.
The last case, non-proportional multiaxial, results in a non-stationary principal stress tensor, its direction is continually changing thereby influencing the crack growth and direction of propagation. In this instance the engineer must be aware of the extent of this directional variation to ascertain the suitability of the analysis. Small angular variations of the tensor result in small errors, however as the angular variations increase the effect on fatigue analysis become more apparent. It is important for the engineer to know what has caused the rotating principal axis in order to ascertain how far to trust the results. In the next section we look at what causes multiaxial stress states and how the angular variation of principal stress tensor can be determined.
There are three causes of rotating principal stresses:
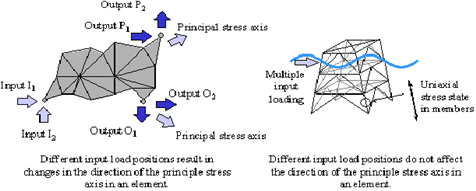
Class I: Rotating Principal Stress Axes Caused by Multiaxial Loading
In some structures multiple input loading will give rise to rotating principal stresses, this is not always the case and so we must have a method of detecting it.
Figure 8‑66 illustrates two examples, one where multiple input loading does affect the stress state, and the other where it does not.
Figure 8‑66 Rotating Principal Stress Axes Caused by Multiaxial Loading
Class I rotating principle stresses can be identified by comparing the direction of the principal stress axes for different load positions. It is worth noting that a non-proportional, multiaxial load state need not result in a rotating principal stress state, we are interested in the 'stress state' not the load state.
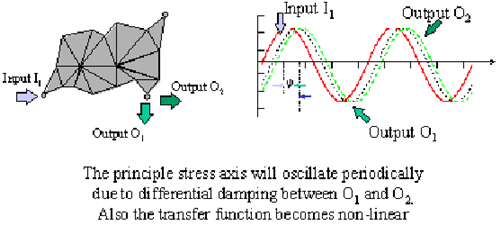
Class II: Rotating Principal Stress Axes Caused by Differential Damping
Differential damping can give rise to a multiaxial stress state where the principal axis is seen to periodically oscillate. For this to be significant then the structure has to exhibit fairly high levels of differential damping, as this is not common for most structures then this potential cause of multiaxiality should not present many problems with most engineering applications. It is still worth noting however, that Class II rotation is commonly accompanied by Class III and in these cases the Class III is usually the cause of the problem.
Figure 8‑67 illustrates the effect. Damping causes a phase lag between input and output frequencies and differential damping between both output components will cause phase lags between O
1 and O
2, hence causing variations in the direction of the principal stress axis.
Figure 8‑67 Rotating Principal Stress Axes Caused by Differential Damping
To see how this effect works consider the complex stress vector
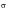
shown in
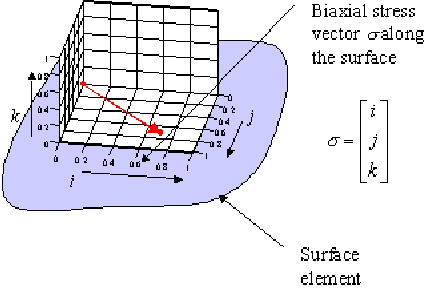
Figure 8‑68. We will deal first of all with a simple biaxial stress state on a surface element where the stress perpendicular to the surface is zero (i.e. k = 0). Later in the text we will deal more generally with the full triaxial case.
Figure 8‑68 Visualizing a Principal Stress Vector On the Surface of a Component
Vector
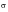
is complex and each element of the vector i, j, and k contains information on the amplitude and phase of the transfer function stress in that particular direction. In an isotropic material with no differential damping, the argument of i, j and k are identical indicating that the components are in phase. Consider now how the stress vector responds to a unit sinusoidal input load, this is illustrated in
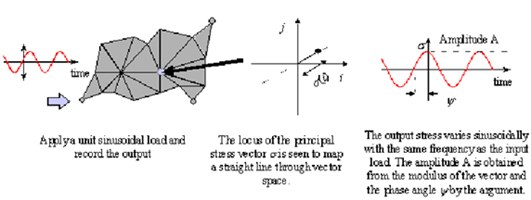
Figure 8‑69.
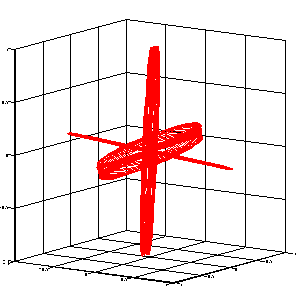
Figure 8‑69 Stress Response Vector For a Component with NO Differential Damping
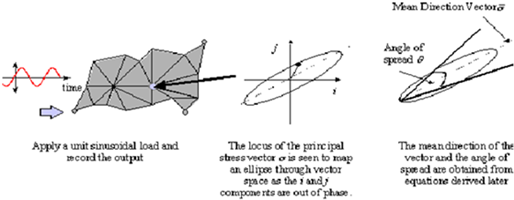
Consider now the stress response to a unit sinusoidal load in a non-isotropic material where the damping properties are different in the i and j directions, this is illustrated in
Figure 8‑70.
Figure 8‑70 Stress Response Vector For a component With Differential Damping.
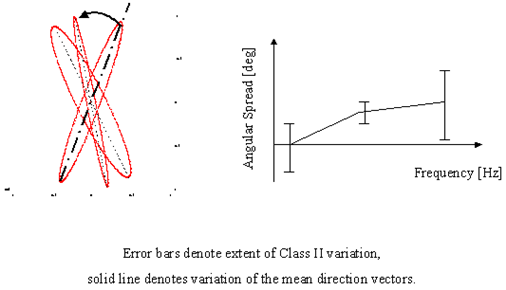
Comparing the spread of the vector for each frequency identifies class II nonstationarity. If this test were positive it would suggest a problem with the actual FE model as most engineering structures exhibit only small damping values.
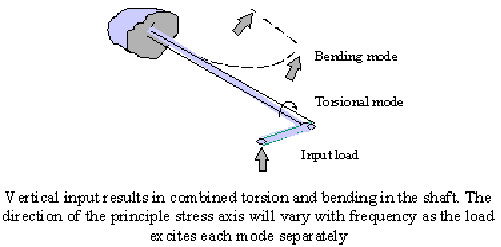
Class III: Rotating Principal Stress Axes Caused by Exciting Vibration Modes
In some structures the direction of the principal axis may be dependent on the frequency of the applied load. This phenomenon can occur when the applied load is exciting more than one mode. As each mode approaches its natural frequency, the stresses associated with that mode increase, thus causing a variation of the principal stress axis.
Figure 8‑71 shows a classic example of Class III nonstationarity, with a simple cantilever beam in combined bending and torsion.
Figure 8‑71 Rotating Principal Stress Axes Caused by Exciting Vibration Modes
Class III nonstationarity is tested by comparing the direction of the principal stress axes for varying frequencies. Differences in the phase angles would indicate frequency dependent rotating principal stresses.
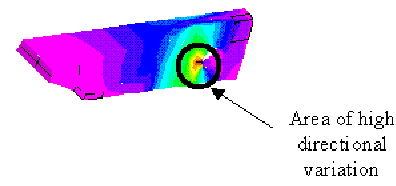
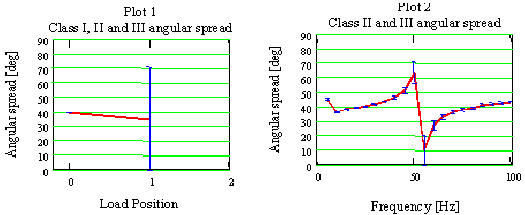
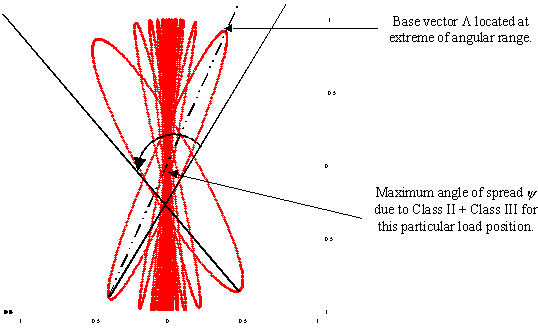
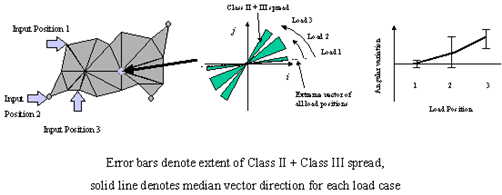
Note: | It might be possible to analyze structures exhibiting this type of behavior if the actual loads lie outside the critical frequency areas. |
In summary, by far the most significant of these three Classes are Classes I and III. Class I is often more apparent in the immediate vicinity of applied loads or a sudden change in structural geometry. Class III will arise where torsion and axial modes are witnessed, but the engineer may find the frequencies affected to be sufficiently distanced from those at which the loads are applied.
Class II seldom arises on its own, this would likely indicate a problem with the model. However, it is common to find Classes II and III occurring together due to the differential damping between two modes being exited near their natural frequency.
Displaying the Angular Variation of the Principal Stresses.
The design engineer needs to determine the extent to which the principal stress tensor rotates at a particular node in order to decide whether to proceed with the analysis at that point or whether to change to a time based multiaxial fatigue analyzer. It is worth noting that although rotating principal stresses may occur in a component in some localized areas these will have no affect on other nodes within the model and the engineer is free to consider this analysis technique in those stable areas. Also, in many instances the designer will have no choice in the analysis technique (maybe time implications, etc.). In this case knowing the extent of the principal stress rotation and the Class causing this will prove crucial to the confidence of the results.
The results of the axis stationarity test are presented in two stages. Firstly, the maximum angular variation is calculated for all three classes and displayed on a contour plot of the finite element model. Areas of high and low rotations can easily be detected and the engineer quickly ascertains whether a problem exists or not. See
Figure 8‑72.
Figure 8‑72 Contour Plot of Principal Axis Stationarity
Should a problem be detected, the engineer will need to ascertain the cause of this, either Class I, II, or III. The cause is easily deduced using two error bar plots, the first discriminates between Class I and the other two classes. The second discriminates between Classes II and III. These are shown in
Figure 8‑73.
Figure 8‑73 Error Bar Plot to Show Extent of Class I, II and III Principal Stress Rotation
Calculating the Angular Variation of Principal Stress Axes
The angle between two real vectors a and b is determined from the scalar product expressed in
(8‑75).
(8‑75)

Where
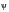
is the angle between the two vectors a and b.
In our implementation, we are dealing with complex vectors where the modulus yields the magnitude of the principal stress and the argument yields its phase relative to the phase of the input load. In this case,
(8‑75) is unsatisfactory and a better definition is obtained from
(8‑76). (The benefit of this definition becomes apparent when calculating Class II situations).
(8‑76)
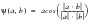
Where
is the angle between the two vectors a and b.
The two error bar plots in
Figure 8‑73 help to distinguish the classes of axis rotation. In the following sections we look at how the values in the plots are determined.
Calculating the Values for Plot 1
For this analysis, we must calculate the maximum angular range of the stress vector for each input load and also show how the median direction vector varies between each input load position.
Figure 8‑74 shows a plot of the loci of the stress vectors over all frequencies for one particular load position. The plot represents a biaxial stress state in the i/j plane, the elliptical orbits show Class II non-stationarity. The total angular spread for Classes II and III is derived from the envelope of the vectors as shown in
Figure 8‑74.
Figure 8‑74 Plot Showing Loci of Unit Stress Vectors and Maximum Angular Spread
To calculate the total angular spread of the principal stress axis, we first need to determine an extreme vector lying at the edge of the range, the angle of every other principal stress vector can then be determined relative to this. This step becomes necessary as we use
(8‑76) to determine the angle y and this returns a scalar value with no indication as to whether the angle is positive or negative. To find an extreme vector we choose any arbitrary vector in the range and proceed to locate the vector with the largest angular deviation from it. Provided that the stress state is biaxial or hydrostatic triaxial then this vector will always be an extreme. (We will look at full triaxial stress states later.) The angle between an arbitrary vector and an extreme
is given in
(8‑77).
(8‑77)
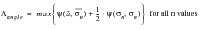
Where
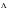 angle
angle is the angle between an arbitrary vector a and an extreme vector
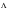
.
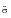
denotes the mean direction vector of
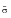
defined as
In other words, the angle between vectors a and
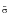 n
n is the angle between their mean directions plus half the angle of spread of vector
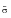 n
n due to the elliptical orbit of the locus.
Having determined an extreme base vector
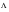
we can proceed to find the next vector with the maximum angle from this. This now gives the total angular spread of the principal stress axis. In this calculation we also need to include the angle given by the elliptical orbits associated with both vectors. The equation is given in
(8‑78).
(8‑78)
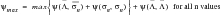
Where
 max
max is the total angular spread.
The Class I axis variation monitors how a principal stress axis rotates with respect to the different input positions. Associated with each load input is an angular spread due to Classes II and III, for Class I analysis we calculate these with respect to a new base vector at the extreme of all the vectors from all frequencies and load positions.
Figure 8‑75 illustrates the point.
Figure 8‑75 Illustrating The Calculation of Class I Principal Axis Rotation
Calculating the Values for Plot 2.
For each load position it is necessary to distinguish between a Class II or a Class III problem. This analysis proceeds along the same lines as that described earlier:
1. Locate a base vector at the extreme of the load position under consideration.
2. Calculate the angle between the base vector and all other mean direction vectors for each frequency giving the Class III drift. (This is represented by the solid line on error bar plot 2.
3. Calculate the angular spread of the elliptical locus for each frequency.
The procedure is illustrated in
Figure 8‑76.
Figure 8‑76 Illustrating The Calculation of Class II & III Principal Axis Rotation
Dealing with Triaxial Stress States
Most fatigue analysis is concerned with surface stresses and these are unlikely to have a triaxial stress state unless acted upon by hydrostatic forces, such as with submarines and pressure vessels. The analysis technique for tracking the principal stress vectors is still valid under these conditions, though it does become unreliable when dealing with a varying triaxial stress state where all three axes rotate. The unreliability is due to the method adopted in determining the extreme base vector. With the full triaxial case, we can no longer assume this is the vector with the greatest deviation from any arbitrary vector in the range.
Figure 8‑77 shows the loci of the principal stresses in a triaxial stress state.
Figure 8‑77 Loci Plot of a Triaxial Stress State