Composite materials are typically made from sheets of materials whose thickness is very much smaller than their width. Therefore, an elementary understanding of surface geometry is essential in order to use these materials effectively.

For the purposes of engineering analyses, surfaces are generally divided into flat plates or curved shells. Compared with plate structures, shells generally exhibit superior strength and stiffness as a consequence of their curvature. Shells have traditionally been difficult to manufacture from conventional materials like aluminum, but are now readily built from plies of reinforcing fabrics which conform or drape relatively easily to surfaces of complex curvature. The potential for optimizing surface geometry leads to weight savings beyond those promised by the increase in mechanical performance alone.

The drapability of reinforcing materials results directly from their ability to shear, allowing the material to cling to surfaces without folding or tearing. It is important to understand the cause of material shear as this both changes the form of the material, and hence its mechanical properties, but also varies the alignment of the fibres with respect to the loads in the surface. The latter factor is especially vital in unidirectionally-reinforced materials where the strength and stiffness along the fibres may be more than ten times greater than in the transverse direction.

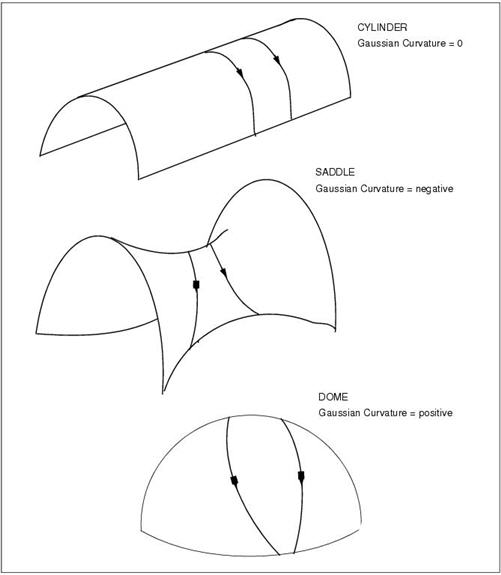
The amount of shear distortion in a sheet of material is dependent on the degree of curvature of the surface and the size of the sheet. The curvature of the surface is conveniently measured by a scalar quantity called the “Gaussian curvature” which is the product of the curvature of the surface in two orthogonal principal directions. For example, the dome has positive Gaussian curvature because the sense of the curvature in two directions at 90 degrees is the same.

Gaussian curvature can be visualized easily by drawing geodesic lines on surfaces. (Geodesic lines are those that are straight in the plane of the surface, such as the meridian of a sphere.) A pair of lines which are parallel at some point will tend to converge, remain parallel or diverge on surfaces of positive, zero and negative curvature respectively.

In contrast, the cylinder has zero Gaussian Curvature as there is no curvature along its axis. All “developable” surfaces (i.e., those that can be rolled up from a flat sheet without the material shearing in its plane) necessarily have zero Gaussian Curvature over their entire area. Finally, a saddle which has curvature in two different directions, has a negative Gaussian curvature.