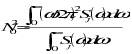XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> 11.2 Basic Random Analysis Theory
Introduction
The information in this section has been adapted from MSC Nastran Advanced Dynamics Analysis User’s Guide (Ref 1) and MSC Nastran 2004 Release Guide (Ref 2). The calculations performed by MSC Random are essentially identical to MSC Nastran and any differences will be noted.
As with MSC Nastran, random response analysis with MSC Random is treated as a data reduction procedure that is applied to the results of a frequency response analysis. First, the frequency response analysis is performed for sinusoidal loading conditions, {Pa}, each a separate subcase, at a sequence of frequencies i. The results are output to a normal XDB results file. At this point MSC Random is used throughout the Patran interface to perform calculations of random responses such as auto and cross power spectral densities and auto and cross correlation functions for all of the result data in the XDB file.
Each loading condition subcase represents a unique random load source, which may be applied to many grid points. Typically, these loads are chosen to be unit loads such as unit “g” loads or unit pressures. The probabilistic magnitude of each load source is defined by spectral density functions on RANDPS entries in the random input file. If the load subcases are correlated, the coupling spectral density is also defined on one or more RANDPS entries. An example of coupled spectral density would be the forces on four wheels of a vehicle traveling over a rough road (see example 3 for Cross Spectrum Input).
Figure 2-1 is a simplified flow diagram for the random analysis. The inputs to the module are the frequency responses, Hja(i), of quantities uj to loading conditions {Pa} at frequencies i, and the auto- and cross-spectral densities of the loading conditions Sa and Sab. The response quantities, Sj, may be displacements, velocities, accelerations, internal forces, or stresses. The power spectral densities of the response quantities are calculated by different procedures depending on whether the loading conditions are correlated or uncorrelated. The spectral densities due to all sources, considered independent, will be combined into one set of outputs.
Figure 11‑2 Flow Diagram for Random Analysis
Theory
The application of frequency response techniques to the analysis of random processes requires that the system be linear and that the excitation be stationary with respect to time. the theory includes a few important theorems which will be reviewed. An important quantity in random analysis theory is the autocorrelation function Rj(), of a physical variable, uj, which is defined by
(11‑1)

Note that R
j(0) is the time average value of
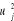
, which is an important quantity in the analysis of structural failure. The one-sided power spectral density S
j() of u
j is defined by
(11‑2)
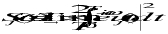
It may be shown (using the theory of Fourier Integrals) that the autocorrelation function and the power spectral density are Fourier transforms of each other. Thus, we define the autocorrelation function in terms of frequency response functions
(11‑3)
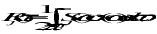
from the mean-square theorem, the rms (root mean squared) magnitude, uj, is
(11‑4)
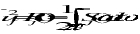
The expected value of the number of zero crossing with positive slope per unit time, or apparent frequency, is a quantity of interest for fatigue analysis. This mean frequency, N0, can be found from the power spectral density;
(11‑5)
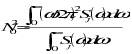
The mean frequency, N0, is thus the root mean square frequency, where the power spectral density is used as a weighing function.
The transfer function theorem states that, if Hja() is the frequency response of any physical variable, uj, due to an excitation source, Qa, which may be a point force, a loading condition or some other form of excitation, i.e., if
(11‑6)
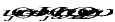
Where uj() and Qa() are the Fourier transforms of uj and Qa, then the power spectral density of the response , is related to the power spectral density of the source, Sa(), by
(11‑7)
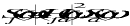
Eq 2-6 is an important result because it allows the statistical properties (e.g., the Auto-correlation function) of the response of a system to random excitation to be evaluated via the techniques of frequency response. Another useful result is that, if sources Q1, Q2, Q3, etc., are statistically independent, i.e., if the cross-correlation function between any pair of sources
(11‑8)
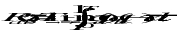
is null, then the power spectral density of the total response is equal to the sum of the power spectral densities of the responses due to individual sources. Thus
(11‑9)

If the sources are statistically correlated, the degree of correlation can be expressed by a cross-spectral density, Sab, and the spectral density of the response may be evaluated from
(11‑10)

Where H*jb, is the complex conjugate of Hjb.
In applying the theory, it is not necessary to consider the sources to be forces at individual points. Rather, an ensemble of applied forces that are completely correlated (i.e., a loading condition) should be treated as a single source. For example, a plane pressure wave from a specified direction may be treated as a source. Furthermore, the response may be any physical variable including internal forces and stresses as well as displacements, velocities, and accelerations.
Cross-Power Spectral Density and Cross-Correlation Functions
For a pair of response quantities, ua(t) and ub(t), the cross-correlation functions between them is defined as
(11‑11)
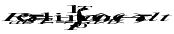
Where ua(t) and ub(t) can be displacement, velocity, acceleration or single-point force responses at the same or different grid points; or stress, strain, and force components in the same of different elements. The cross-correlation functions have the following relation
(11‑12)

The cross-power spectral density (cross-PSD) of ua(t) and ub(t) is defined as;
(11‑13)

(11‑14)
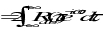
And Rab() is related to Sab() by the relation
(11‑15)
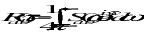
The cross-PSD Sab() is a complex-valued function of angular frequency . The following relations hold for the cross-PSDs.
(11‑16)
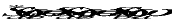
Where Sab*() is the complex conjugate of Sab(). If we denote Sab() by its real and imaginary parts as
(11‑17)
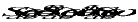
From (2-15), we can see that Sab(R)() is an even function and Sab(I)() is an odd function of , i.e.
(11‑18)
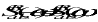
(11‑19)
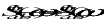
Substituting (2-17) and (2-18) into (2-14), we get
(11‑20)

If the system is subject to multiple sources of excitation, the cross-PSD of responses ua(t) and ub(t) is related to the PSDs of excitation sources by the frequency response function as
(11‑21)

Where Haj() is the frequency response function of ua(t) corresponding to the excitation source Qj(t), Hbk*() the complex conjugate of Hbk() , and Sjk() the cross-PSD of excitation sources when j k. If the two different excitation sources Qj and Qk are not correlated, we have Sjk() 0.
The aforementioned equations of cross-PSDs and cross-correlation functions become the ones for auto-PSDs and auto-correlation functions when ua(t) = ub(t).
The calculation of the cross-correlation function from 2-18 is carried out by numerical integration based on the trapezoidal approximation.
Cumulative Root Mean Square (CRMS)
The cumulative RMS (CRMS) shows how the RMS value is accumulated through frequency range. CRMS shows the frequency range that contributed the most in the total RMS value. The CRMS uj() of a random response quantity uj(t) at a set of selected frequency point is defined as
The Root Mean Square (RMS) of a random response quantity uj(t) is defined as
(11‑22)
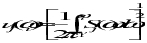
, i = 1,2, …, N (2-21)
Coherence Function or Schwarz's Inequality
The coherence function (sometimes called the coherency squared function or Schwarz’s Inequality) is defined as
(11‑23)
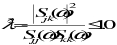
MSC Random will check for the input and will print out the warning message in “job-name”.out file.
Numerical Integration Using Log-Log Approximation
MSC Random, by default, uses logarithmic integration to calculate RMS value. MSC Nastran, on other hand uses linear integration by default. In order to use logarithmic integration in MSC Nastran, use “Param, Rmsint, LogLog” (See Ref 6). The logarithmic approach yields more accurate results if PSDF curve is straight line in an integration sub-domain in a Log-Log scaled coordinate system and also will produce better results with fewer frequency points compared to the trapezoidal approximation of PSDF using Linear coordinate system (See Ref 2, sec 3.7 for more details).
Von Mises Stress in Random Analysis
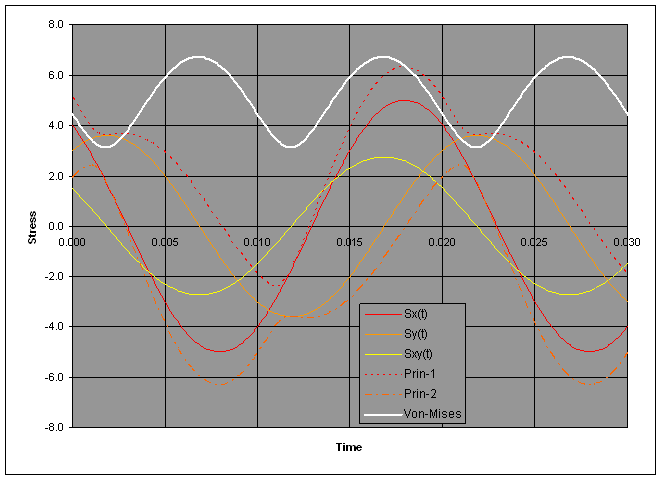
The RMS of basic stress tensor can not be used to calculate von Mises stresses. The probability distribution of von Mises stress is not Gaussian, nor is it centered about zero as basic stress tensor is. This can be demonstrated by the specific example. Fig 2-2 shows the harmonic response of basic tensor, Sx, Sy and Sxy, in time domain. The von Mises and Principal stresses are calculated at each time steps from basic tensor. Ref 5 have demonstrated efficient way to calculate peak von Mises stresses from harmonic stress tensors, however, as shown in figure, von Mises stress does not oscillate about zero. The principal stresses are periodic but not harmonic. The von Mises stress is a scalar quantity and the basic tensor has same direction at all times whereas principal stresses change the direction at every time steps.
Figure 11‑3 Time domain representation of harmonic response.
Ref 3 and 4 outline the method of calculating von Mises PSD response. Ref 3 discusses computing von Mises PSD using Modal Approach whereas Ref 4 computes von Mises PSD directly from PSD-matrix of stress tensor. The MSC Random uses the approach from Ref 4 since it is applicable to both Modal Frequency Response Analysis and Direct Frequency Response Analysis.