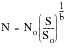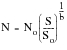XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> Total Life (S-N) Analysis
It has been recognized, since 1830, that a metal subjected to a repeated or fluctuating load will fail at a stress level lower than that required to cause fracture on a single application of the load. The nominal stress (S-N) method was the first approach developed to try to understand this failure process and is still widely used in applications where the applied stress is nominally within the elastic range of the material and the number of cycles to failure is large. From this point of view, the nominal stress approach is best suited to that area of the fatigue process known as high-cycle fatigue. The nominal stress method does not work well in the low-cycle region where the applied strains have a significant plastic component. In this region, a strain-based methodology must be used.
Stress Cycles
Before looking in more detail at the nominal stress procedure it is worth considering the general types of cyclic stresses which contribute to the fatigue process.
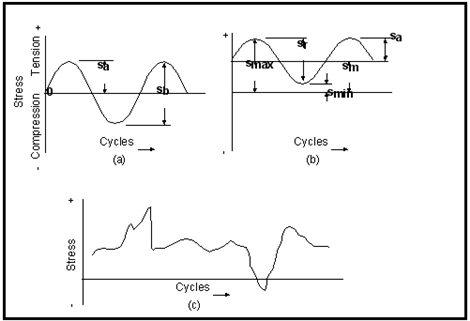
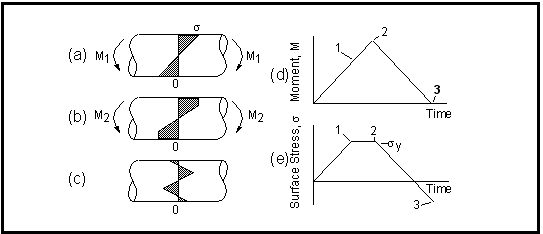
Figure 15‑7 details some typical fatigue stress cycles.
Figure 15‑7 Typical Fatigue Stress Cycles,
(a) Fully Reversed (b) Offset, (c) Random
In
Figure 15‑7(a) illustrates a fully-reversed stress cycle with a sinusoidal form. This is an idealized loading condition typical of that found in rotating shafts operating at constant speed without overloads. For this kind of stress cycle, the maximum and minimum stresses are of equal magnitude but opposite sign. Usually tensile stress is considered to be positive and compressive stress negative.
Figure 15‑7 (b) illustrates the more general situation where the maximum and minimum stresses are not equal. In this case they are both tensile and so define an offset for the cyclic loading.
Figure 15‑7 (c) illustrates a more complex, random loading pattern which is more representative of the cyclic stresses found in real structures.
From the above, it is clear that a fluctuating stress cycle can be considered to be made up of two components, a
static or steady state stress
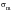
, and an alternating or variable stress
amplitude,
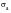
. It is also often necessary to consider the stress
range,
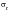
, which is the algebraic difference between the maximum and minimum stress in a cycle.
(15‑2)
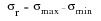
The stress amplitude,
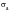
, then is one half the stress range.
(15‑3)
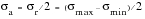
The mean stress, is the algebraic mean of the maximum and minimum stress in the cycle.
(15‑4)
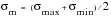
Two ratios are often defined for the representation of mean stress, the stress or R ratio, and the amplitude ratio A.
(15‑5)
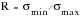
(15‑6)
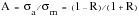
Table 15‑5 illustrates some R values for common loading conditions.
Table 15‑5 R ratio | Loading Condition |
R > 1 R = 1 0 < R < 1 R = 0 R = -1 R < 0 R infinite | Both σmax and σmin are negative. Negative mean stress. Static loading. Both σmax and σmin are positive; Positive mean stress, |σmax| > |σmin|. Zero to tension loading, σmin = 0 Fully-reversed loading, |σmax| = |σmin|; zero mean stress. |σmax| < |σmin|, σmax approaching zero. σmax equal to zero. |
|
|
|
|
|
|
The S-N Curve
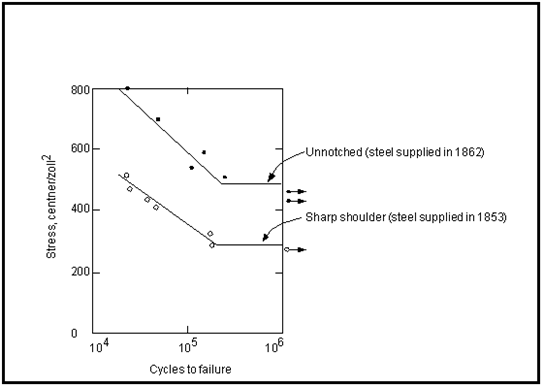
Between 1852 and 1870, the German railway engineer August Wöhler set up and conducted the first systematic fatigue investigation.
Figure 15‑8 S-N Data Reported by Wöhler
(Note, 1 centner = 50 Kg, 1 zoll = 1 inch, 1 centner /
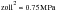
.)
Wöhler conducted cyclic tests on full-scale railway axles and also on small-scale bending, torsion, and push-pull specimens of several different materials. Some of Wöhler’s data, shown in
Figure 15‑8, are for Krupp axle steel and are plotted, in terms of nominal stress vs. cycles to failure, on what has become known as the S‑N diagram. Typically, the S-N relationship is determined for a specific value of Sm, R or A. Note that in dealing with the nominal stress approach, the convention is that nominal stress is usually referred to as S and localized stress by the Greek counterpart,
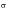
.
Procedure for Determining the S-N Curve
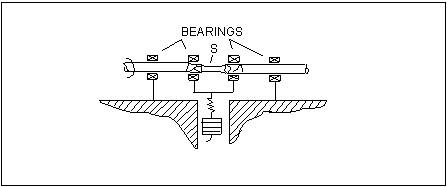
Most determinations of fatigue properties have been made in completely reversed bending (i.e., R = –1), by means of the so-called rotating bend test. One example is the R. R. Moore test, which uses four-point loading to apply a constant moment to a rotating (1750 rpm) cylindrical hourglass-shaped specimen. See
Figure 15‑9. Specimens, which are typically between 6 to 8 mm in diameter in the test section, are usually polished to a mirror finish prior to testing.
Figure 15‑9 The R.R. Moore Fatigue Testing Machine
The stress level at the surface of the specimen is calculated using the elastic beam equation, even if the resulting value exceeds the yield strength of the material.
(15‑7)
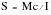
where:
S | | the nominal stress acting normal to the cross-section |
M | | the bending moment |
c | | the distance of the surface from the neutral axis |
I | | the moment of inertia |
For the circular section of the R. R. Moore specimen, the beam equation reduces to:
(15‑8)
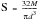
where:
d | | the diameter of the specimen. |
The usual laboratory procedure for determining an S-N curve is to test the first specimen at a high stress, about two thirds of the static tensile strength of the material, where failure is expected in a fairly small number of cycles. The test stress is decreased for each succeeding specimen until one or two specimens do not fail before at least 107 cycles. For materials which exhibit it, the highest stress at which no failure occurs, a runout is taken to be the fatigue limit. For situations where an infinite life design requires a probability of survival to be associated with it, more complex testing and analysis procedures, such as the Prot and staircase methods, have been developed to determine the mean and variance of the fatigue limit. For materials which do not exhibit a fatigue limit, tests are usually terminated between 107 and 108 cycles, and the concept of an endurance limit at either 107 or 108 cycles defined.
The S-N curve is usually determined through the use of about 15 specimens. However, it is generally found that results are accompanied by a large amount of scatter and some form of statistical analysis should be applied, see
The Statistical Nature of Fatigue, 1390 for more details.
S-N data are nearly always presented in the form of a log-log plot of alternating stress, amplitude Sa or range Sr, versus cycles to failure, with the actual Wöhler line representing the mean of the data. Certain materials, steels for example, display a fatigue limit, Se, which represents an alternating stress level below which the material has an infinite life. For most engineering purposes, infinite is taken to be 1 million cycles. Great care must be exercised when designing on the basis of a fatigue limit, since it has a nasty habit of disappearing due to periodic overloads, corrosion, and elevated temperature.
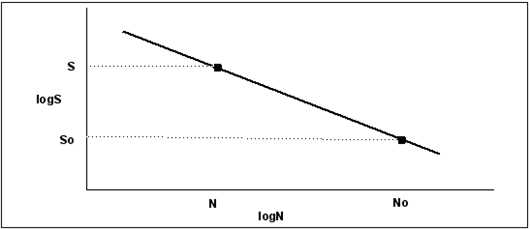
Figure 15‑10 Idealized Form of the S-N Curve
When plotted on log-log scales, the relationship between alternating stress, S, and number of cycles to failure, N can be described by a straight line,
Figure 15‑10. The slope of the line, b, (after Basquin, a prominent worker who first proposed the law) can be derived from the following:
(15‑9)
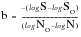
(15‑10)
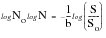
(15‑11)
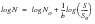
(15‑12)
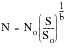
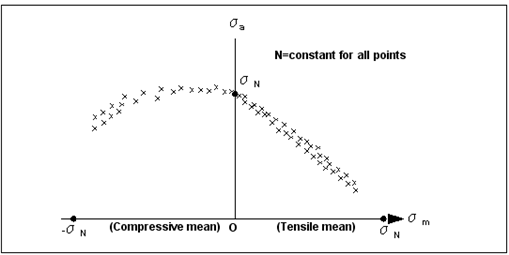
Sometimes, for convenience, the term 1/b is replaced by the letter k,
(15‑13)
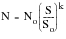
The above equation says that if we know the Basquin slope, b, and any other coordinate pair (No,So), then for a given stress amplitude S, the number of cycles can be calculated directly. Typically, No is taken to be 106 cycles and the corresponding stress amplitude is taken to be an endurance limit, usually denoted as Se or S6, so that the above equation may be rewritten as:
(15‑14)
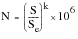
Example 1: A Simple Life Estimation
For a material with an endurance limit of 250 MPa, and a Basquin slope, b, of -0.1, calculate number of cycles to failure at a stress amplitude of 300 MPa. Under these conditions,
(15‑14) gives:
Limits of the S-N Curve
As previously mentioned, the S-N approach is applicable to situations where cyclic loading is essentially elastic.
Figure 15‑11 Typical S-N Curves for Ferrous and Nonferrous Metals
This means that the S-N curve should be confined on the life axis to numbers greater than about 10,000 cycles in order to ensure no significant plasticity is occurring.
Indeed, great care must be taken in using the above S-N equations in situations where lives less than 10,000 cycles are being estimated.
Figure 15‑11 shows typical S‑N curves for both ferrous and nonferrous metals. The points to note in
Figure 15‑11 are the limits of the logN axis, the presence of a fatigue limit for the mild steel and the absence of a fatigue limit for the aluminum alloy. Because both materials represented in
Figure 15‑11 have relatively low yield stresses, the life axis is confined to begin at 105 cycles at which point the alternating stress is about 350 and 300 MPa respectively for the two alloys.
Tensile Properties and the S-N Curve
Through many years of experience, particularly with steels, empirical relationships between fatigue and tensile properties have been developed. These relationships are not soundly based in science. However, they remain useful tools for engineers for assessing fatigue performance. When the S-N curves for a number of different steels of varying strengths are plotted as the ratio of endurance limit (i.e., the stress amplitude at 106 cycles), S6, to ultimate tensile strength, Su, all the curves tend to all fall onto a single curve which implies that:
(15‑15)
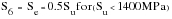
and
(15‑16)
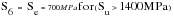
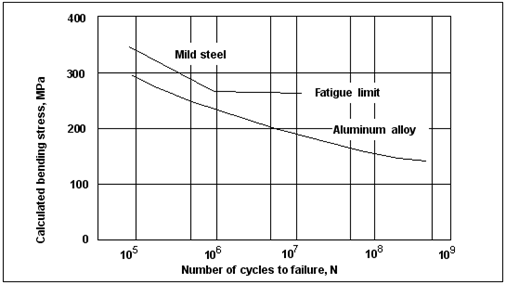
Figure 15‑12 Generalized S-N Curve for Wrought Steels
In addition to this, the stress at 103 cycles, S3, can be approximated by 0.9 Su and so, utilizing these approximations, a generalized S-N curve can be generated for wrought steels, see
Figure 15‑12.
Methods of representing the S-N curve in the range 1 to 103 cycles have been developed but they must be treated with extreme caution. They usually use some percentage of the ultimate strength, Su, or true fracture stress,
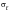
, as a measure of the stress amplitude at either 1 or 1/4 cycles. The main difficulty with employing this approach is that the deduced S-N curves are extremely flat in the low-cycle region, and this makes estimates of life particularly inaccurate. The reason for this apparent flatness is the large plastic strain which results from the high load levels. Low-cycle fatigue analysis is best treated by strain-based procedures which account for rather than ignore the effects of plasticity.
The Influence of Mean Stress
As previously mentioned, most basic fatigue data are collected in the laboratory by means of testing procedures which employ fully reversed loading (i.e., R = –1). However, most realistic service situations involve nonzero mean stresses. It is, therefore, very important to know the influence that mean stress has on the fatigue process so that the fully reversed laboratory data can be usefully employed in the assessment of real situations.
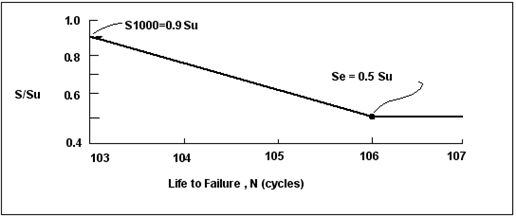
Figure 15‑13 High-Cycle Fatigue Data Showing the Influence of Mean Stress
Fatigue data collected from a series of tests designed to investigate different combinations of stress amplitude and mean stress are characterized in
Figure 15‑13 for a given number of cycles to failure. The diagram plots the mean stress, both tensile and compressive, along the x-axis and the alternating constant stress amplitude along the y-axis. This kind of representation was first proposed by Haigh and is therefore commonly referred to as the Haigh diagram.
The stress amplitude at zero mean stress, Sn, corresponds to the stress amplitude at N cycles to failure as measured by the fully-reversed fatigue test. The failure data points tend to follow a curve which if extrapolated would pass through the ultimate tensile strength, Su, on the mean stress axis. Notice that the influence of mean stress is different for compressive and tensile mean stress values. Failure appears to be more sensitive to tensile mean stress, than compressive mean stress. When available, data of the type illustrated above are collated into what are commonly referred to as master diagrams for a particular material.
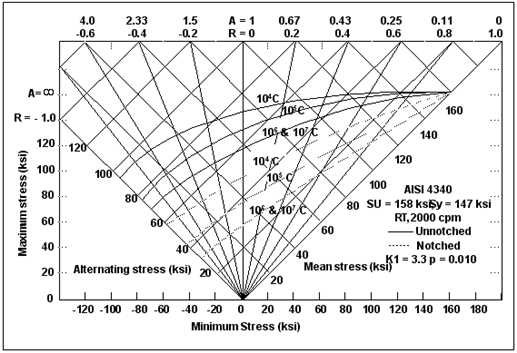
Figure 15‑14 illustrates the master diagram for SAE 4340 from the U.S. Department of Defense MIL Handbook-5.
Figure 15‑14 Master Diagram for SAE 4340
Since the tests required to generate a Haigh or master diagram are quite expensive, several empirical relationships which relate alternating stress amplitude to mean stress have been developed. These relationships characterize a material through its ultimate tensile strength, Su, and are very convenient. For infinite life design strategies, the methods use various curves to connect the endurance limit, Se, on the alternating stress axis to either the yield stress, Sy, ultimate strength, Su, or true fracture stress,
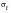
, on the mean stress axis. Of all the proposed relationships, two have been most widely accepted (i.e., those of Goodman and Gerber).
(15‑17)Goodman:
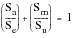
(15‑18)Gerber:
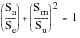
Experience has shown that actual test data tends to fall between the Goodman and Gerber curves (Goodman joining Se to Su by means of straight line and Gerber by means of a parabola). For most design situations where R « 1 (i.e., small mean stress in relation to the alternating stress), there is little difference between the two relationships. However, when R approaches 1 (i.e., nearly equal mean and alternating stresses, the two relationships show considerable differences). Unfortunately, little or no experimental data exist to support one approach over the other and so typically, the recommendation would be to select the approach which provides the most conservative lives in a given situation.
Example 2: Correcting for Mean Stress Effects
A component is subjected to a maximum cyclic stress of 750 MPa and a minimum of 70 MPa. The steel from which it is manufactured has an ultimate tensile strength, Su, of 1050 MPa and a measured endurance limit, S6, of 400 MPa. The fully reversed stress at 1000 cycles is 750 MPa. Using both the Goodman and Gerber mean stress correction procedures calculate the component life.
The first step is to calculate the stress amplitude, Sa, and the mean stress, Sm,using equations
(15‑3) and
(15‑4).
(15‑19)
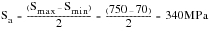
(15‑20)
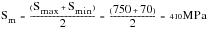
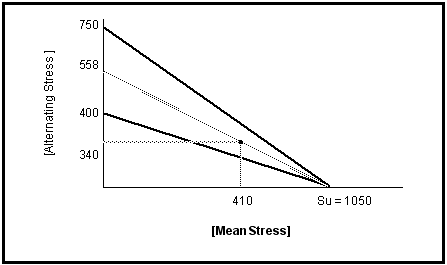
A Haigh diagram for the Goodman correction procedure can now be constructed for constant lives of 106 and 103 cycles. This is done by connecting the endurance limit, S6, and the stress at 1000 cycles, S3, respectively, on the alternating stress axis with the ultimate tensile strength, Su, on the mean stress axis (see
Figure 15‑15). The stress conditions on the component calculated above, Sa = 340 and Sm = 410, can be plotted on the diagram and a line drawn from Su to the alternating stress axis. This line represents the constant life line for the component at all combinations of stress amplitude and mean stress. The line intersects the fully reversed axis at a stress Sn = 558 MPa.
Figure 15‑15 The Haigh Diagram
It should be noted that this stress can also be calculated directly from the Goodman equation
(15‑17):
(15‑21)
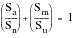
It will be recalled that the S-N curve is given by equation
(15‑13),
and so for the conditions defined at 103 and 106 cycles,
and so
and for Sn = 557.8, the life can be calculated from:
The Gerber correction can be used in a similar way, i.e.,
and
Factors Influencing Fatigue Life
A standardized rotating bend test (such as the R.R. Moore test) is used to determine a baseline S-N relationship for a polished specimen of approximately 6mm diameter loaded under conditions of fully reversed bending. If the fatigue or endurance limit measured by these means be denoted by S'e then the actual limit for a real component, Se, must reflect all the modifications that come about in moving from a laboratory specimen to a component. For steels in particular, several empirical relationships have been developed which can account for the variation in Se as a result of the following:
• Component size
• The type of loading
• The effect of notches
• The effect of surface finish
• The effect of surface treatment
The usual way to account for these effects is through the calculation and application of specific modifying factors so that:
(15‑22)
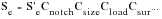
where reciprocal of the product, Cnotch Csize Cload Csur, is collectively known as the fatigue strength reduction factor Kf, i.e.,
(15‑23)
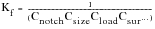
The approach tends to be conservative and the corrections are usually only applied at the endurance limit, the modifications required for the rest of the S-N curve are ill-defined. Typically, the procedure is to pivot the S-N curve about the 1000 cycles point, see
Figure 15‑16.
Figure 15‑16 Modification of the S-N Curve
It is very important to remember that all the modification factors are empirical, conservative and mostly only applicable to steels. They provide little or no fundamental insight into the fatigue process itself other than providing approximate trends. In particular, they should not be used in areas outside their measured applicability.
The Influence of Component Size
Fatigue in metals results from the nucleation and subsequent growth of crack-like flaws under the influence of an alternating stress field. This view leads to the concept of failure commencing from the weakest link, the most favorably orientated metal crystal for example, and then growth through less favorably orientated grains until final failure. Intuitively, it would seem reasonable to suppose that the larger the volume of material subjected to the alternating stress, the higher the probability of finding the weakest link sooner. Actual test data do confirm the presence of a size effect particularly in the case of bending and torsion.
The stress gradient built up through the section, in bending and to a lesser extent in torsion, concentrates more than 95% of the maximum surface stress to a thin layer of surface material. In large sections, this stress gradient will be less steep than in smaller ones, and so the volume of material available which could contain a critical flaw will be greater leading to reduced fatigue strength. The effect is quite small for axial tension where the stress gradient is absent. The value for Csize can be estimated from one of the following, if the diameter of the shaft is < 8mm:
(15‑24)
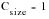
if the diameter is between 8 mm and 250 mm:
(15‑25)
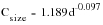
The effect of size is particularly important for the analysis of rotating shafts such as might be found in vehicle powertrains.
For situations where components do not have a round cross section, an equivalent diameter, deq, can be calculated for a rectangular section width, w and thickness, t, undergoing bending from:
(15‑26)
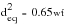
The Influence of Loading Type
Fatigue data measured according to one regime, axial tension for example, may be “corrected” to represent the data that would have been obtained had the test been carried out in some other loading methodology such as torsion or bending. Recall that the R.R Moore test calls for fatigue tests to be carried out under conditions of fully-reversed bending.
The values of Cload to be used in conjunction with the endurance limit, Se, in moving from one loading condition to another are detailed in
Table 15‑6.
Table 15‑6 6
Measured Loading | Target Loading | Cload |
Axial to | Bending | 1.25 |
Axial to | Torsion | 0.725 |
Bending to | Torsion | 0.58 |
Bending to | Axial | 0.8 |
Torsion to | Axial | 1.38 |
Torsion to | Bending | 1.72 |
In addition to influencing the endurance limit, loading conditions can also influence the Basquin slope, b. This effect is usually taken into account by modification of the stress at 103, S3, as well as Se. The following factors can be used to define C'load, the S3 modification factor, see
Table 15‑7.
Table 15‑7 3
Measured Loading | Target Loading | Cload |
Axial to | Torsion | 0.82 |
Bending to | Torsion | 0.82 |
Torsion to | Axial | 1.22 |
Torsion to | Bending | 1.22 |
The Influence of Surface Finish
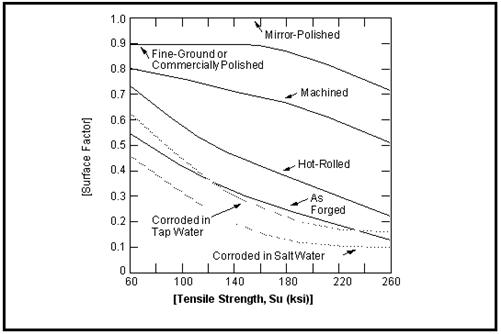
A very high proportion of all fatigue failures nucleate at the surface of components and so surface conditions become an extremely important factor influencing fatigue strength. The usual standard by which various surface conditions are judged is against the polished laboratory specimen. Normally, scratches, pits, machining marks influence fatigue strength by providing additional stress raisers which aid the process of crack nucleation. Broadly speaking, high strength steels are more adversely affected by a rough surface finish than softer steels, for this reason the surface correction factor, Csur, is strongly related to tensile strength. The surface finish correction factor is often presented on diagrams that categorize finish by means of qualitative terms such as polished, machined or forged, see
Figure 15‑17.
Figure 15‑17 Surface Finish Correction Factor for Steel Components
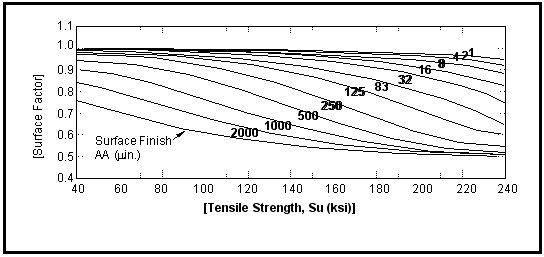
Figure 15‑18 The Effect of Surface Roughness on Surface Finish Factor
It is worth noting that some of the curves presented in
Figure 15‑17 include effects other than just surface finish. For example, the forged and hot-rolled curves include the effect of decarburization.
Other diagrams present the surface factor in a more quantitative way by using a quantitative measure of surface roughness such as R
A, the root mean square, or AA the arithmetic average, see
Figure 15‑18. Values of surface roughness associated with each of the manufacturing processes are readily available in handbooks, as an example consider
Table 15‑8.
Table 15‑8 Type of finish | Surface Roughness (microns) |
Lathe-formed Partly hand polished Hand Polished Ground Superfinished Ground and polished | 2.67 0.15 0.13 0.18 0.18 0.05 |
|
|
|
|
|
Figure 15‑19 Residual Stress in a Beam
The Influence of Surface Treatment
As in the case of surface finish, surface treatment can have a profound influence on fatigue strength, particularly the endurance limit. Surface treatments can be divided broadly into mechanical, thermal, and plating processes. The important point to note with all three is that the net effect of the treatment is to alter the state of residual stress at the free surface. In the first two processes, by providing a compressive layer, and in the case of plating, by providing a tensile residual stress.
Residual stresses arise when plastic deformation is not uniformly distributed throughout the entire cross-section of the component being deformed.
Figure 15‑19 represents a metal bar whose surface has been deformed in tension by bending so that part of it has undergone plastic deformation. When the external force is removed, the regions which have been deformed plastically prevent the adjacent elastic regions from complete elastic recovery to the unstrained condition. In this way, the elastically deformed regions are left in residual tension, and the plastically deformed regions must be in a state of residual compression. For many purposes, residual stress can be considered identical to the stresses produced by an external force. Thus, the presence of a compressive residual stress at the surface of a component will have the effect of decreasing the likelihood of fatigue failure.
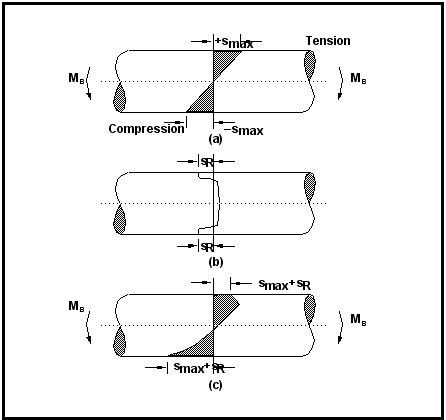
Figure 15‑20 Superposition of Applied and Residual Stresses
Figure 15‑20 illustrates the effect schematically.
Figure 15‑20(a) shows an elastic stress distribution in a beam with no residual stress. The typical residual stress distribution associated with shot peening is detailed in
Figure 15‑20(b). Note that the compressive stress at the surface must be compensated by an equivalent tensile stress over the interior of the cross section. In
Figure 15‑20(c), the distribution due the algebraic summation of the residual and applied stresses is shown. Observe that the maximum tensile stress at the surface has been reduced by the amount of the residual stress. Furthermore, note that the peak tensile stress has now been moved to the interior of the beam. The magnitude of this stress will depend on the gradient of the applied stress and the residual stress distribution. Also note that under these conditions, subsurface crack initiation becomes a possibility.
Mechanical Treatments
The main commercial methods for introducing residual compressive stresses are cold rolling and shot peening. Although some alteration in the strength of the material occurs as a result of work hardening, the improvement in fatigue strength is due mainly to the compressive surface stress. Surface rolling is particularly suited to large parts and is frequently used in critical components such as crankshafts and the bearing surface of railway axles. Bolts with rolled threads typically possess twice the fatigue strength of conventionally machined threads.
Shot peening, which consists of firing fine steel or cast iron shot against the surface of a component, is particularly well suited to processing small mass produced parts.
It is important to remember that cold rolling and shot peening have their greatest effect at long lives. At short lives they have little or no effect.
As with other modifying factors, the effect of these mechanically induced compressive stresses can be accounted for by the use of correction factors which can be used to adjust the endurance limit Se. Typically the factor associated with peening is about 1.5-2.0.
Plating
Chrome and nickel plating of steel components can more than halve the endurance limit due to the creation of tensile residual stresses at the surface. These tensile stresses are a direct result of the plating process itself. As in the case of mechanically induced surface stresses, the effect of plating is most pronounced at the long life end of the spectrum and also with higher strength materials.
The deleterious effect of plating can be reduced by introducing a compressive residual stress prior to the plating process by either shot peening or nitriding. An alternative approach might be to anneal components after plating and thereby relieve the tensions.
Electroplating may also cause a shortening of the fatigue life through the mechanism of hydrogen embrittlement. Hydrogen ions are produced at the surface of the metal during plating. For high-strength steels, these ions enter the large steel microstructure and then combine into the molecular hydrogen, H2, causing high stresses under cyclic loading and accelerating fatigue failure. Such effects are difficult to model analytically. In practice, the preventative action of baking the component after plating to release the hydrogen is often used.
Thermal Treatments
Thermal treatments are processes which rely on the diffusion of either carbon, carburizing, or nitrogen, nitriding, onto and into the surface of a steel component. Both species of atoms are interstitial (i.e., they occupy the spaces between adjacent iron atoms), and thereby both increase the strength of the steel and, through volumetric changes, cause a compressive residual stress to be left on the surface. Carburizing is commonly carried out by packing the steel components within boxes which contain carbonaceous solids, sealing to exclude the atmosphere and heating to about 900° C for a period of time which depends on the depth of the case required. Alternatively, components may be heated in a furnace in the presence of a hot carburizing gas such as methane. This process has the advantage that it is quicker and more accurate. In addition, the carburizing cycle may be followed up by a diffusion cycle, with no carburizing agent present, which allows some of the carbon atoms to diffuse further into the component and so reduce gradients.
The nitriding process is very similar in nature to gas carburizing, except that, in this case, ammonia gas is used and the components are soaked at lower temperatures. Typically 48 hours at about 550 degrees centigrade will provide a nitrided case depth of about 0.5 mm. Nitriding is particularly suited to the treatment of finished notched components such as gears and slotted shafts, the effectiveness of the process is illustrated in
Table 15‑9.
Table 15‑9 Geometry | Endurance Limit (MPa) |
not nitrided | nitrided |
Unnotched Semicircular notch V notch | 310 175 175 | 620 600 550 |
|
|
Example 3: To Shot Peen or Not?
From a particular vehicle, as heat treated, low alloy leaf springs (manufactured to a tensile strength of 1500 MPa), are failing in service, albeit after some considerable time, but nevertheless within the lifetime of the vehicle. Service measurement has shown that the loading is of the type from zero to a maximum stress of about 770 MPa (i.e., R = 0). The question to be answered is, will shot peening the springs prior to installation make the problem go away?
The springs have a section measuring 40 mm by 5 mm. From tables of surface roughness, Csur has been determined to be about 0.75 for the “as heat treated” condition and about 0.58 for the “shot peened” condition. Measurements have shown that shot peening introduces a compressive residual stress of about 550 MPa.
From the ultimate strength, Su = 1500 MPa, S'e can be estimated to be 750 MPa.
For the “as heat treated” condition the modification factor required to correct for the section size of the springs can be estimated by first calculating the equivalent diameter, deq, associated with the rectangular cross section from
(15‑26):
deq2 = 0.65 w t = 0.65 x 40 x 5 = 130
deq = 11.4 mm
and since deq > 8 mm, Csize can now be computed from
(15‑25):
Csize = 1.189 x 11.4-0.097 = 0.94
Since, in operation, the leaf springs are loaded only in bending, CL is equal to 1.0.
We are now in a position to calculate the modified magnitude of endurance limit, Se.
Se = S'e x the product of all the modifying factors
Se = 750 x 0.94 x 1.0 x 0.75
Se = 529 MPa
For the loading condition defined by R = 0, the amplitude of the alternating stress, Sa, and the mean stress, Sm, must be equal. By setting Sa = Sm, the allowable stress level, S, for the as heat-treated material can now be calculated from the Goodman equation
(15‑17).
(Sa / Se) + (Sm / Su) = 1
(S / 529) + (S / 1500) = 1
S = 391 MPa
and the maximum allowable stress for infinite life would be
Smax = Sa + Sm = 2 S = 782 MPa
This figure is uncomfortably close to the operational maximum stress of 770 MPa and so clearly we do not have an infinite life design; we must expect to have some failures in service.
The procedure so far has been useful since it has helped us verify the calculation procedure being used and provided some confidence in the methodology. We are now in a position to estimate the effect of shot peening.
In the shot peened condition, the modified magnitude of endurance limit, Se is given by:
Se = S'e x the product of all the modifying factors
Se = 750 x 0.94 x 1.0 x 0.58
Se = 409 MPa
As in the as heat-treated case, for R = 0, the amplitude of the alternating stress, Sa, and the mean stress, Sm, are equal and the Goodman equation can be used to calculate the allowable stress. By subtracting the compressive residual stress from the mean stress, the peening operation is taken into account,
S = 439 MPa
and the maximum allowable stress for infinite life would be
Smax = Sa + Sm = 2 S = 878 MPa
The calculated maximum working stress for shot peened springs is significantly higher than both the equivalent as heat treated stress and the operational stress. From this, we could justifiably conclude that shot peening to the extent which produces residual compression of 550 MPa would be sufficient to provide the leaf spring with an infinite service life.
Application in MSC.Fatigue
MSC.Fatigue supports two types of stress-life curve. The first is the nominal or component S-N curve where the stress plotted on the Y‑axis is not the actual stress where failure occurs (i.e., there is a built-in geometric stress concentration factor, Kt ). The use of this type of S-N curve is only valid when the stress in a nominal or reference area is used to compute lives. This approach takes no account of localized plasticity effects such as might be found at a stress-raiser. The effects of such discontinuities must be taken into account through the S-N damage curve itself. Each S-N curve, therefore, must reflect the overall “structural” characteristics of the detail under investigation.
The second type of S-N curve is the local stress or material S-N curve. This curve has associated with it a Kt value of 1.0 (i.e., the stress on the Y‑axis is a local stress which causes fatigue). No reference area is needed as the results at each node or element may be used directly.
The S-N approach must be used when basic material data are unavailable, or one or more of the basic assumptions embodied in the more fundamental local stress‑strain approach are considered invalid. Typical examples would be the treatment of welded structures or complex joints, rivets or spot welds and composites. In addition) some companies, due to the extensive use of the stress-life method in past years, a large quantity of S-N curves and experience has been accumulated. In this case, the stress-life method offers compatibility with previous work and so may be more appropriate.
The Measured Loading Environment
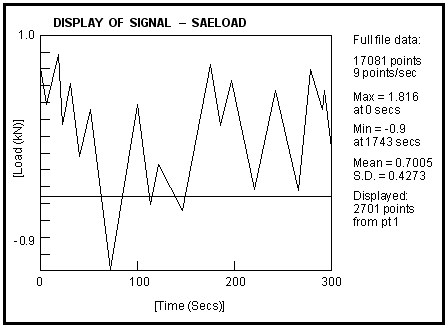
MSC.Fatigue requires a representation of a load time history in order to define the loading environment to which a component or structure is subject, such as shown in
Figure 15‑21.
Figure 15‑21 A Load Time Series
It is very important to ensure that these measured load histories are indeed representative of the service environment experienced by the component in terms of both amplitudes and sequence. If, for example, the main source of fatigue damage is due to occasional “overloads” such as the bump of a wheel on a pothole or the “cold-hot-cold” (startup-run-shutdown) cycle of a large engine, as opposed to the cyclic loads associated with continuous smooth operation, then large errors and misinterpretations can arise.
Definition of the S-N Curve
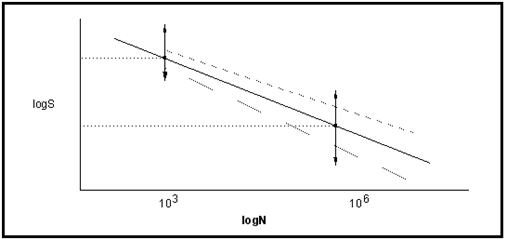
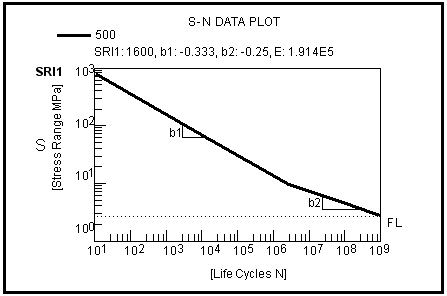
Figure 15‑22 The S-N Fatigue Damage Curve
The basic equation for the S-N curve is:
(15‑27)
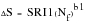
which may be written as:
(15‑28)
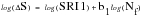
ΔS | | Nominal stress range |
SRI1 | | Stress range intercept of the life line |
SRI2 | | Stress range intercept of second life line |
b1 | | Slope of the first life line |
b2 | | Slope of the second life line |
Note that in
Figure 15‑22 the slope of the life line changes, with the second slope, b2, being shallower than the first. This “knee” or fatigue transition point, as it is sometimes called, punctuates the change in slope and typically occurs at about 107 cycles. The second slope can have any value between the first slope, b1, and zero. In the case that it is zero, the transition point represents a fatigue limit below which no further damage will accumulate.
The equation of the second life line will of course be defined by:
(15‑29)
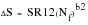
If b2 is non-zero, a stress-based fatigue limit, FL, may be defined to cutoff any further fatigue damage; all three features can be distinguished in
Figure 15‑22.
Because of the complexity and often the variability of the test pieces used, together with the difficulties of controlling local stresses and strains, the degree of scatter in the measured lives can be quite high. It is usual, therefore, to apply some statistical methods to account for this variability. MSC.Fatigue takes this scatter into account through a consideration of the standard error of log (Nf).
The standard error of log (Nf) is calculated in the following way:
(15‑30)
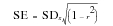
SE | | Standard error of log(Nf) |
SDx | | Standard deviation of log(Nf) from the regression analysis |
r | | Correlation coefficient from the regression analysis |
By the use of this statistic, a whole family of life curves, centered around the “mean life line”, may be constructed. It is usual to consider three standard deviations on either side of the mean. The lower limit represents 99.9% confidence that, for a given stress range, failure will not occur after less cycles than those which correspond to that stress. The mean life line provides 50% confidence and in the case of the upper line only 0.15% confidence that the component will survive.
Figure 15‑23 The 3-SD Confidence
Analytical Procedure
Since the stress-life method in MSC.Fatigue makes no attempt to model localized plasticity, the analytical procedure used is relatively straightforward and may be summarized as follows:
1. By means of linear static FEA, derive the local stress time history from the load time histories. This includes superpositioning of multiple FEA/load time history load cases (or use stress time history directly from linear transient or forced vibration FE analysis). However, it is important to ensure that the S-N data applies to the situation being modeled; most S-N curves are for nominal stress, not local stress.
2. Extract the fatigue cycles in the local stress time history by means of the rainflow algorithm.
3. Assess the damage contribution of each cycle by referring to the selected damage curve.
4. Linearly sum the damage associated with each cycle by using Miner’s rule.
Account for Nominal Mean Stress
Nominal S-N curves can be either structure, component or specimen based and are used to provide damage data for complex situations which otherwise could not be characterized. This gives rise to different procedures for accessing the S-N curve, depending on the situation being considered. Indeed, the British Standards Institution has tried to formalize some of these procedures in the document BS5400 Pt. 10. The main differences between the various procedures lie in the treatment of mean stresses and the damage contribution of cycles with “small” ranges. The total life analyzer in MSC.Fatigue offers five different procedures:
1. Ignore the Effect of Mean Stress
In this mode of operation, the stress-life analyzers in MSC.Fatigue estimate the damage for each cycle and takes no account of its mean stress. If the stress range of the cycle is below the fatigue limit then no damage will be accumulated irrespective of the relative magnitude of any other cycles which may be present.
2. Account for Mean Stress According to BS5400 Pt.10, Welded
In this mode of operation, the stress-life analyzers in MSC.Fatigue estimate the damage for each cycle and do not take into account the effects of mean stress.
Specific S-N curves are used for the BS5400 welded analysis and these are referred to as weld classes. These damage curves are known to MSC.Fatigue by the following names:
CLASSB, CLASSC, CLASSD, CLASSE, CLASSF,
CLASSF2, CLASSG, CLASSW, CLASSS and CLASST
3. Account for Mean Stress According to BS5400 Pt.10, Non-Welded
In this mode of operation, the stress-life analyzers in MSC.Fatigue estimate the damage for each cycle and takes account of the effects of mean stress by reducing compressive stress amplitudes to 60% of their measured values.
Specific S-N curves are used for the BS5400 non-welded analysis. These are referred to as classes and are known to MSC.Fatigue by the following names:
CLASSB, CLASSC, CLASSD, CLASSE, CLASSF,
CLASSF2, CLASSG, CLASSW, CLASSS and CLASST
These S-N curves are in fact the same as those used in the welded analysis. The difference in the non-welded analysis lies in the treatment of compressive stresses.
4. Account for Mean Stress According to Goodman
In this mode of operation, the stress-life analyzers in MSC.Fatigue estimate the damage for each cycle and account for the effects of mean stress by reducing the allowable applied stress amplitudes in a linear way for both positive and negative mean stresses. This procedure was first proposed by Goodman and can be summarized as follows:
(15‑31)
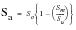
Sa | | The allowable stress amplitude. |
So | | The allowable stress amplitude at zero mean stress. |
Sm | | The mean stress. |
Su | | The ultimate tensile stress. |
If the stress range of the cycle is below the fatigue limit, as defined by the FL parameter, then no damage will be accumulated irrespective of the relative magnitude of any other cycles which may be present.
Account for Mean Stress According to Gerber
In this mode of operation, the stress-life analyzers in MSC.Fatigue estimate the damage for each cycle and account for the effects of mean stress by reducing the allowable applied stress amplitudes in a quadratic way for both positive and negative mean stresses. This procedure was first proposed by Gerber and can be summarized as follows:
(15‑32)
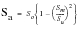
Sa | | The allowable stress amplitude. |
So | | The allowable stress amplitude at zero mean stress. |
Sm | | The mean stress. |
Su | | The ultimate tensile stress. |
If the stress range of the cycle is below the fatigue limit, as defined by the FL parameter, then no damage will be accumulated irrespective of the relative magnitude of any other cycles which may be present.
Linear Damage Summation
A constant amplitude, S-N curve represents a set of tests at constant stress range (
S) together with associated lives. Operation at a stress range (
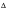
S1) will result in failure in say N1 cycles. Operation at the same stress range for a number of cycles less than N1, Nj say, will result in a smaller fraction of damage, Dj, which is often referred to as a partial damage. Operation over a spectrum of different stress ranges, results in a partial damage contribution Di from each stress cycle,
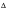
Si. Failure is then predicted when the sum of these partial damage fractions reaches unity so that:
(15‑33)
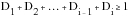
The Palmgren-Miner rule asserts that the partial damage at any stress range
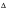
S1, is linearly proportional to the ratio of the number of cycles of operation to the total number of cycles that would produce failure at that stress level,
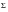
(F(n
1,Ν
1)). For example:
(15‑34)
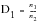
Failure is predicted then if:
(15‑35)
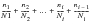
or
(15‑36)
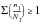
The above equations represent a statement of the linear damage rules used by both the stress-life and local strain fatigue life processors in MSC.Fatigue. Experience shows that linear damage summation is somewhat of an over simplification of reality. The most important shortcoming is that no account is made of the sequence in which strain levels are experienced, and damage is assumed to accumulate at the same rate for a given strain level regardless of prehistory. In particular, it appears that large strain amplitudes which precede smaller ones, cause the smaller cycles to become more damaging than expected. The net result is that in the first instance, the Miner’s sum
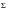
(F(n,Ν)) is measured to be less than 1 and in the latter case it becomes greater than 1. Since most service environments involve quasi-random loading sequences, the use of the Palmgren‑Miner linear damage rule summing to a constant of 1 is mostly satisfactory.
Important: | BS 5400 Pt 10 attempts to cope with these effects by asserting that if there are no cycles with a stress range greater than the stress corresponding to 1 x 107 cycles, then no damage will be accumulated. If, on the other hand, even one cycle exceeds this stress, then damage will be accumulated for ALL other cycles. This correction takes into account the observed behavior when a crack growing cycle occurs, subsequent previously non-damaging cycles start to increment the crack size (i.e., cause damage). This is particularly true for welded structures which are always already cracked. The choice of the 1E7 cycles point reflects the fact that the stress at this point is close to the threshold for crack advance. If, on the other hand, even one cycle exceeds this stress, then damage will be accumulated for ALL other cycles. |
Factor of Safety Analysis
When fatigue was first recognized in the mid 1800s, the solution to fatigue problems was to find a load below which fatigue failures didn’t occur. This worked well as far as eliminating fatigue failures, but it made structures heavy and expensive. The direction of fatigue research since then has been to allow engineers to make products lighter and more highly optimized. The safe life and fail-safe philosophies came from this recognition by engineers that product weight and cost must be reduced without increasing risk of unexpected failure. This was especially true for aircraft structures which would never leave the ground if they were designed for no cracks (i.e., no fatigue damage). In other words, the fatigue life of some products must be finite.
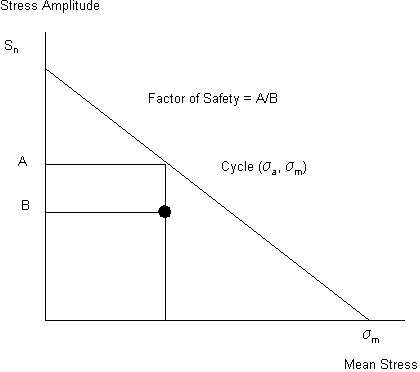
However, there is still a class of structures where fatigue lives are essentially infinite or at least beyond any available fatigue test data. Typically these include components from high speed rotating machines such as internal combustion engines and gas turbines. In order to assess the fatigue life of “infinite life” structures, it has been found most useful if a measure is obtained of the difference between the working stress and the fatigue limit stress (a stress below which no fatigue damage is incurred). Often this is expressed as a ratio of fatigue limit/working stress and this ratio is known as the “factor of safety.” This simple methodology is ideal for hand calculations using idealized loading but for realistic variable amplitude loading, a more realistic approach is required.
Stress Based Calculation
Taking the basic factor of safety concept as a ratio of the applied stress to the fatigue stress, it is possible to introduce a mean stress correction based on the Goodman or Gerber rules.
Goodman Based Factor
(15‑37)Factor of Safety =
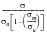
This equation may be modified to include corrections for surface finish (Csurf) and size effects (Csize). These factors take values less than 1.0. An additional notch sensitivity factor may be included (Kf) which is a multiplier of the applied stress amplitude.
(15‑38)Factor of Safety =
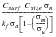
σn | | is the stress at life n |
σa | | is the stress amplitude of the cycle |
σm | | is the mean stress of the cycle |
σu | | is the ultimate strength of the material |
The normal way to select Sn is to choose a target life and to obtain the corresponding stress from an S-N curve, extrapolating the curve to the required life if necessary.
The factor of safety can be illustrated graphically on the Goodman diagram as shown in
Figure 15‑24.
Figure 15‑24 Factor of Safety Illustrated on the Goodman Diagram
Gerber Based Factor
This is the same as the Goodman except the Gerber mean stress correction is applied.
(15‑39)Factor of Safety =
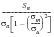
By also calculating the factor of safety for each cycle in a random loading history, the stress-based factor of safety may be used with realistic loading in a meaningful way.
MSC.Fatigue calculates factors of safety for all cycles in a time history at each location (node or element) and reports the lowest value computed. The correction factors for surface treatment and finish are obtained from the Lipson (9) empirical data and are related to the ultimate strength of the material.
Life-Based Calculation
The life based calculation is in fact a calculation to find the magnitude of stress scaling factor which will cause failure in a specific design life. Since the scaling factor is applied to all cycles it is an overall factor of safety. This approach is far better suited to calculating meaningful factors of safety for random loading.
This approach to calculating a scaling factor is used in MSC.Fatigue in the Factor of Safety module for multi-location computation and also in Design Optimization where the scaling parameter optimization calculates the value of a factor at one location (node/element).
Other Factors Influencing Safety
The calculations described above compute a stress scaling factor either using a stress based or life based methodology. It should be remembered that there are other factors contributing to the life of the product. For example, a change in the material may reduce the factor of safety. This may be explored more fully using the Design Optimization tools in MSC.Fatigue or by submitting a new job with edited input data.