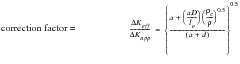XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> Crack Growth Analysis Theory
In general engineering, the possibility of crack-like defects being present at the start of service life has to be recognized. This is particularly true when asking oneself the question “what if we can’t be sure the structure is not cracked?” (i.e., the safest assumption is that the biggest crack that nondestructive testing cannot reliably find is present). Even if the component is not cracked to start with, the remaining life after initiation may be significant or possibly dominant with respect to the total life. Furthermore, for inspection related activities, the remaining life of a component discovered to be cracked during inspection needs to be determined so that decisions regarding serviceability can be supported by reliable life estimations.
In low-stress (linear elastic) situations, the growth of fatigue cracks governs useful life leading to the “defect tolerance approach” to design which necessarily also implies regular inspection and assessment. In service, fatigue loading is nearly always random and the operating environment is nearly always corrosive or aggressive in nature.
Diagnosis or life estimation can only be achieved in one of two ways: laboratory testing under accurately simulated service conditions of geometry, loading and especially environment, or life estimation from quantitative models of crack growth processes. Laboratory testing is very expensive and, because of the time dependent corrosion influence which prohibits test acceleration, it is also very time consuming. For example, an offshore platform designed to withstand 108 cycles in a 30-year life would require a 30-year test at 0.2 Hz to validate the design. Computer-based estimation methodologies can perform the same validation with equal accuracy in a small fraction of the time at a small fraction of the cost.
Basic Principles of Fracture Mechanics
The branch of engineering science concerned with linear elastic fracture mechanics (LEFM) is by no means a new one. The earliest work in the UK dates back to Inglis (1913) but the major developments took place following the research by Griffith at RAE in 1920, and Irwin in the USA in 1956, and LEFM has since flourished.
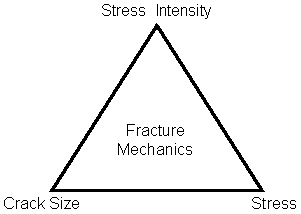
The driving force for a crack to extend is not the strain or stress but the stress intensity factor, universally known as K. This is not to be confused with the stress concentration factor, Kt or with the strain hardening exponents k or k'. The stress intensity factor embodies both the stress and the crack size and uniquely describes the crack tip stress field independent of global geometry. The relationship may be viewed as a triangle:
Figure 7‑54 The Fracture Mechanics Triangle
The triangle may be solved by knowing two of the three corners to derive the third. For example, the material toughness, KIC, and the NDT crack size limit may be known and hence the working stress may be derived to provide safety against fracture.
The relationship between K, applied stress (S) and crack size (a) is:
(7‑11)
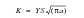
The compliance function, Y, describes the geometry of the structure, component or specimen in which the crack exists. It assumes a value 1 for a defect buried in an infinite body and 1.12 for a surface crack in a semi-infinite body. For finite-sized bodies (i.e., real structures), Y may be seen as a geometric correction which takes a general form:
(7‑12)
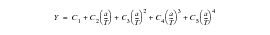
though it may take a much more complex mathematical description in some cases.
In fatigue analysis, again the stress intensity factor provides the driving force for crack growth in the sense that the rate of crack growth, da/dN, is governed by the cyclic range of K,
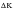
. The two are related by a crack growth “law”, the best known being the Paris Law derived by Paul C. Paris at Lehigh University in 1960:
(7‑13)
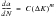
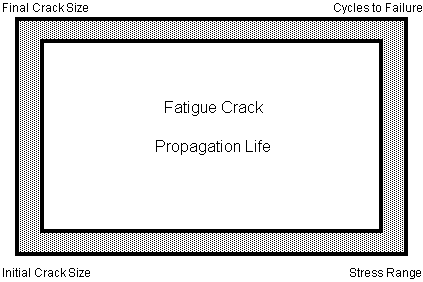
In terms of fatigue crack growth and overall life, a rectangular rather than a triangular representation is used:
Figure 7‑55 The Fatigue Crack Propagation Rectangle
Here we have a relationship between fatigue stress range and fatigue life, in the same way as in an S-N curve approach, but we now also have the initial and final crack sizes and indeed all the crack sizes in between these limits throughout the fatigue crack propagation period. In a similar way to solving the triangle, the fatigue crack propagation rectangle can be solved by declaring the three known corners to derive the unknown fourth.
This relationship may be expressed with the following equations:
(7‑14)
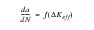
(7‑15)
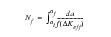
The crack growth prediction model in MSC Fatigue relies on the approximating assumptions that fatigue crack growth can be represented by a simple law:
(7‑16)
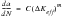
and that the stress intensity factor range can be derived from the solution:
(7‑17)
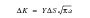
If the geometric compliance function, Y, is assumed to be constant and independent of crack length, a, then integration of
(7‑16) is straight forward. This latter assumption is only strictly true for a very few cases such as a surface crack in an infinite plate. However, it is a quick way of assessing the crack growth performance of a structure.
Substituting
(7‑16) in
(7‑17) and integrating leads to:
(7‑18)
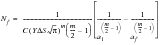
except for the special case where m equals exactly two when:
(7‑19)
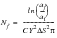
(7‑18) represents a relationship between fatigue life (Nf), stress range (
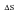
), initial crack size (ai) and final crack size (af). Note that from
(7‑18), af could be infinite and still give a finite fatigue life indicating the relative unimportance of the final crack size. The stress range can be a constant amplitude value or a CA value equivalent to a variable sequence calculated as a weighted average (known as the Weighted Average Stress Range or WASR).
MSC Fatigue Crack Growth Models
The cycle-by-cycle fatigue crack growth prediction module calculates the crack extension, da, in each cycle of a sequence of cycles and adds it to the current crack size. This process proceeds until the failure condition is reached or a preset crack size is achieved. The driving force for crack growth in each cycle is the effective range of stress intensity,
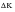
. In each cycle, the apparent or applied
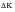
is calculated from the stress range, the crack size and the geometry of the component or structure under consideration. This is then modified to effective
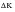
to account for the possible occurrence of:
• crack closure
• history effects
• notch effects
• environmental influence
• static fracture mode contribution
Consequently, the crack propagation life is accurately modeled and this can only be achieved on a cycle-by-cycle basis.
The module may be viewed as part of a greater whole in which a complete case is analyzed using stress-time information, geometric descriptions, and materials response characteristics to produce a prediction that can be subsequently postprocessed and in particular, interpolated.
There are many applications of this approach including: design analysis, pre‑prediction of test programs, defect tolerance assessment, inspection related strategy, failure investigation, and decision support.
The basic premise of the fracture mechanics approach to fatigue relies on the “similitude concept” which adopts the simple belief that if the K is the same, the response is the same. In fatigue terms, the similitude applies to the cyclic range of K,
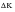
, and the “response” is the rate of fatigue crack growth. It should be clearly understood that even though the growth of macroscopic fatigue cracks is governed by linear elastic fracture mechanics, the microscopic crack extension process by fatigue still necessitates local plasticity. At the tip of a fatigue crack, there are two plastic zones, one for monotonic shear the other for reversed shear, whose sizes depend on the ratio of (
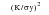
. These crack tip plastic zones are assumed to be negligibly small in relation to crack size, especially for high strength materials, but essential to the fatigue crack growth process.
To undertake a fatigue crack growth life prediction, it is necessary to adopt a cycle‑by-cycle approach and to have a good knowledge of the service loading environment, the appropriate properties to describe materials response, a geometric description and the means of combining this information into a coherent model of the fatigue crack growth process.
The Service Environment
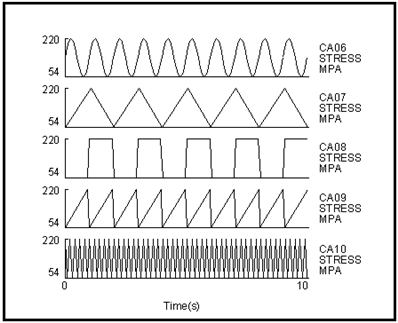
The cycle-by-cycle fatigue crack growth modeling requires a sequence of cycles to be extracted from a representative stress time history. Representative here means not only the sequence of stresses but also the durations, cyclic frequencies, and waveforms. These help to define the environmental effects in corrosion fatigue and the corrosive medium itself should also be characterized in terms of composition, temperature, etc.
Figure 7‑56 Multi-file Display of Stress Histories with Different Frequencies and Waveforms
For example, slower frequencies produce faster crack growth rates, on a da/dN basis, and sine waveforms give faster rates than square waveforms. A multi-file display of stress histories with different frequencies and waveforms is shown in
Figure 7‑56. A stress time history is computed at a node by applying the local scaling. The stress time history is then cycle counted, including reordering in preparation for processing by the main crack growth analyzer.
Geometric Description
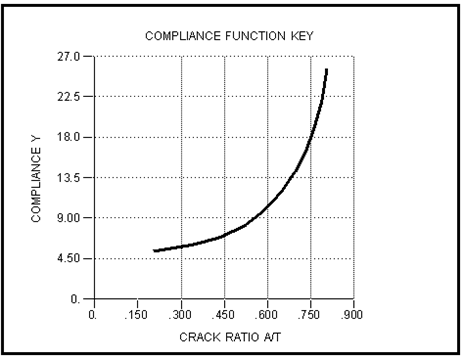
The geometric description of a component or engineering structure is accomplished by means of the appropriate stress intensity solution. This is a mathematical description of the relationship between K, stress (range), and crack size for the geometry in question and many solutions have been derived and documented. The most useful of these are contained in the MSC Fatigue compliance function library module, PKSOL.
This compliance function converts the value of K for each successive loading cycle according to the current crack size. An example of a compliance function is shown in
Figure 7‑57.
Figure 7‑57 An Example of a Compliance Function
Materials Response
The material response is modeled by measuring fatigue crack growth rates as a function of
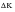
in constant load amplitude laboratory tests using small scale specimens. These can be carried out under the correct environmental conditions and then the similitude concept is invoked to apply the data to large scale components and structures. Also, the fatigue crack growth threshold characteristics and the material fracture toughness are measured using the same type of specimens and all these tests are standardized (e.g., in BSI and ASTM Standards).
The parameters which characterize the materials response in terms of fatigue crack growth have been measured for many materials, in standard tests, and reported in the literature. Until now, no materials database has been constructed in a commercial crack growth prediction software package. The materials response parameters required for crack growth prediction using MSC Fatigue are contained within the materials database and may be viewed using the database manager, PFMAT.
Cycle-by-Cycle Approach
The cycle-by-cycle approach has been adopted as the only way in which fatigue crack growth can be accurately modeled. In each fatigue cycle in turn (the correct order must be preserved), the apparent
is calculated from:
(7‑20)
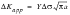
where
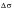
is the stress range of the cycle, a is the current crack size, and Y is the compliance function obtained from the relevant lookup table generated for the geometry in question by the K solution library module, PKSOL. This value of
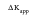
has to be modified if necessary to account for the effects of potentially complicating features until the effective
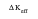
, the driving force that the crack tip actually experiences, is derived. Only then can the crack extension, the amount of crack growth or damage, be calculated simply from the Paris Law (Ref. 10.) as:
(7‑21)
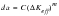
This is added to the current crack size and the process repeated until the crack growth life is exhausted.
Note that this approach disregards all other crack growth laws developed since the original Paris Law, to account for complexing effects, such as Forman’s Law for static fracture modes (Ref. 11.) and the Klesnil and Lukas correction for threshold (Ref. 12.). The Paris Law holds if, and only if, the effective
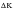
is used and all possible complicating features are modeled through effective
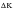
.
The various mechanistic models leading to mathematical descriptions of complex fatigue crack growth behavior are essentially derived from extensive ECSC sponsored research work carried out at British Steel, Swinden Laboratories, involving more than 25 man-years effort and nearly $2 million. The research work is reported ((Ref. 13.) through (Ref. 22.)) in detail including the results of hundreds of tests designed to validate the predictive models.
For each of the features or mathematical models, a description is given in the following sections:
Initial Crack Size
The initial crack size, to which individual cyclic crack extensions are cumulatively added, may be preset but often is unknown. A minimum initial crack size is modeled in MSC Fatigue to ensure that:
1. the crack size is not too small to be handled by the concepts of fracture mechanics as implemented in the MSC Fatigue crack growth analyzer (i.e., it does not violate the assumption of an isotropic continuum by being smaller than a metallurgical feature such as grain size).
2. the crack size at the start of the propagation phase is equal to the crack size at the end of the initiation phase (i.e., critical location fatigue analysis can be combined with fracture mechanics crack growth analysis with ensured continuity to give total fatigue life).
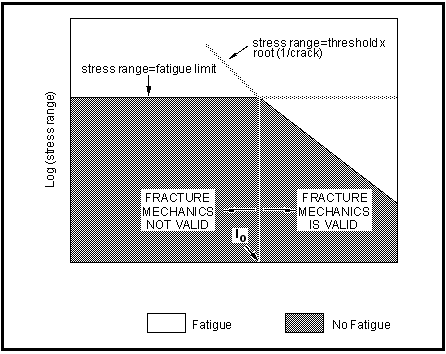
The minimum crack size is derived from the so called “short crack parameter” which is calculated from the “Kitagawa Diagram”. An example of a Kitagawa Diagram, which relates threshold stress and threshold
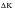
to fatigue crack size is given in
Figure 7‑58.
Figure 7‑58 An Example of a Kitagawa Diagram for Fatigue
The short crack parameter, is given by:
(7‑22)
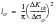
where
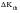
is the threshold
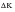
value, and l
o is taken to be the minimum initial crack size. It is in fact calculated in each cycle using the value of
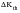
for the stress ratio, R, of that cycle for other purposes, but for the minimum initial crack size it is calculated for R = 0.
Crack Closure and Thresholds
Crack closure can be caused by a number of mechanisms including plasticity, oxide, roughness, corrosion product, metallurgical transformation and incompressible viscous fluids. Starting from the viewpoint that a crack cannot grow when it is closed, then if crack closure occurs at a level, Kcl, that is above Kmin in the cycle, the effective range of stress intensity becomes:
(7‑23)
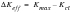
The crack growth rate, da/dN, will be reduced as the driving force that the crack tip experiences is reduced from
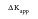
to
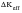
. In the limit, as
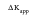
is reduced, Kmax reaches Kcl and
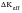
becomes zero; crack growth ceases but there remains a positive applied
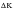
,
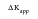
, identified with the threshold for fatigue crack growth,
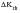
.
Experimental measurements of crack closure (or opening) level are often made by use of crack mouth displacement gauges or back face strain gauges. In threshold testing, the measured closure level is subtracted from the apparent
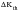
to still leave a positive result, sometimes termed the “intrinsic” threshold. In fact, this is erroneous as only the mechanical closure level is remotely measured (plasticity induced closure) but not the crack tip oxide induced closure. At high stress ratio, R (=Kmin/Kmax), the mechanical closure mechanisms produce Kcl below Kmin but thresholds induced by oxide lead to an approximately constant value of 2MPaR(m) for steels (Ref. 20.).
Applying the logic that at threshold (zero growth rate), the effective
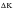
is zero then the overall closure level can be obtained directly from:
(7‑24)
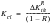
It must be appreciated that measured
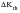
values are linked to a cut off growth rate (10-11 m/c) not zero, though the error is small due to the steepness of the growth rate curve in the rear threshold region.
If the closure level, Kcl, is a constant for a particular stress ratio, then in
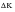
increasing tests (and service situations) the closure effect peters out to nothing as Kmin rises above Kcl so that
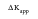
and
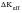
are equal.
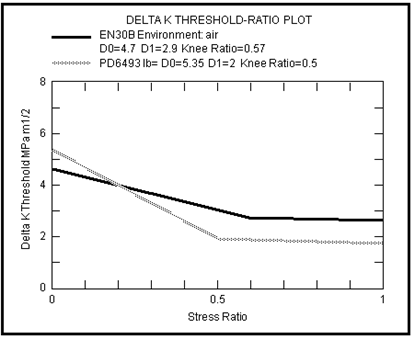
The closure level, which defines the threshold
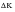
, manifests itself as a stress ratio effect on
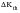
: higher R (higher mean stress) gives lower
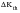
values. It has been found from a wide ranging survey of measured threshold values (Ref. 20.) that the relationship can be described by the equation:
(7‑25)
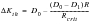
| | Threshold ΔK at a particular R value |
D0 | | Threshold ΔK at R=0 |
D1 | | Threshold ΔK as R->1 |
R | | Stress ratio for the 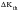 in question |
| | Value of R above which 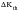 is constant and equal to 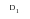 |
The appearance of the dependence of
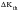
on R is as shown in
Figure 7‑59, which is taken from the database module PFMAT.
Short Cracks
A logical progression from the previous section on crack closure is to consider the apparently anomalous behavior of short cracks. It is well-established that short cracks grow at faster rates and at lower
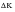
values than would be projected by long crack data and thresholds. Broadly speaking, this is because short cracks have less closure (especially plasticity induced closure) associated with them and indeed may have no threshold at all.
A definition of what is “short” and what is “long” arises from the Kitagawa Diagram (see previous section on initial crack size). Clearly if the cyclic stress range is above the fatigue limit,
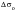
, then fatigue failure will eventually occur implying zero threshold for growth whatever the defect size. For crack sizes smaller than lo, conventional fracture mechanics is unsafe in its prediction of no growth and the use of K is dubious as the crack size may well be less than the microstructural features such as grain size, pearlite colony spacing, etc. The parameter lo thus defines the boundary between short and long cracks and takes values typically in the range 0.01 to 1 mm for steels where high strength steels take the smallest values.
Obviously, because short cracks grow faster, they very quickly become long cracks. As they do so, the plastic deformation wake builds up the crack closure level to that pertaining to long cracks. Mechanistically, it could be suggested that short cracks are not anomalous; long cracks are, because of the closure phenomena associated with them.
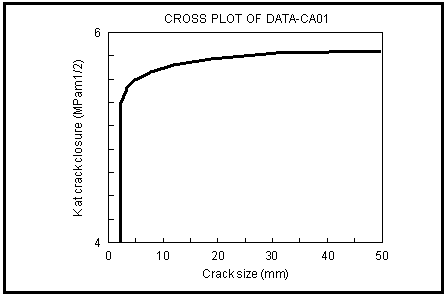
Short crack growth is not modeled in MSC Fatigue in its present form. However, the crack length dependence of the crack closure level is taken into account. The derivation of the formula in
(7‑26) is given by Austen (Ref. 20.), but it describes how the closure level, Kcl, depends on Kmax (because of the plasticity effect) and on crack size in relation to lo.
(7‑26)
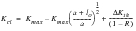
Note that it reduces to
(7‑24), the long crack value of Kcl when a is very much greater than lo. An example of the buildup of crack closure level with increasing crack size is shown in
Figure 7‑60.
Figure 7‑60 The Buildup of Crack Closure Level with Increasing Crack Size
Notches
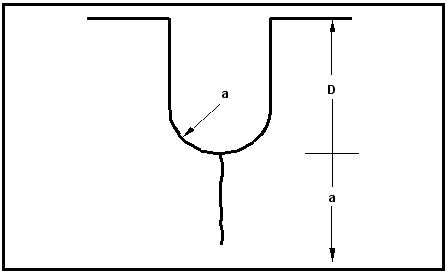
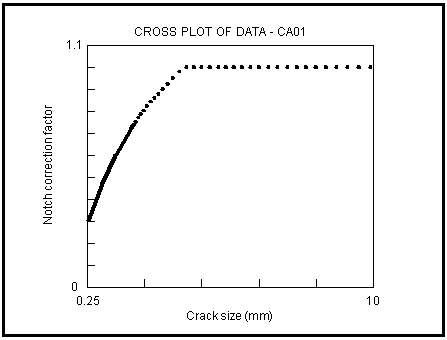
To account for cases where fatigue cracks grow from notches, it is necessary to modify the fracture mechanics description of the crack tip stress field. The presence of the notch overrides the crack tip K solution when the crack is close to the notch but, as the crack grows by fatigue, it escapes from the notch influence. Therefore, it is inappropriate to simply multiply the stress range by the stress concentration factor and equally inappropriate to ignore the notch presence in the K solution. A mathematical model is required in which the notch correction factor varies with crack size and disappears as the crack escapes from the notch influence. Cracks near notches behave like short cracks and a model developed to meet these requirements (Ref. 20.) incorporates the short crack parameter, lo (see previous sections).
Figure 7‑61 Schematic Illustration of a Crack at a Notch
Referring to
Figure 7‑61 for definition of terms, the procedure is to calculate
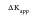
assuming the notch is part of the crack, based on a notional crack size equal to a+D. Then this value is reduced by a correction factor to account for the fact that the notch is not a sharp crack but has a significant root radius,
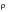
. The full derivation is given elsewhere (Ref. 20.); the formula built into MSC Fatigue to account for notch effects is:
ΔKeff | | Effective ΔK at the crack tip |
ΔKapp | | Remotely applied or apparent ΔK |
a | | Crack size |
D | | Notch depth |
r | | Notch root radius |
ρc | | Root radius of a sharp fatigue crack |
lo | | Short crack parameter |
The correction factor is less than unity and the formula correctly reduces to unity for a sharp notch
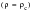
. The factor reaches unity when the crack escapes from the notch; the crack size at this point is given by:
(7‑27)
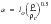
a cannot be less than lo so that the minimum correction factor is:
minimum correction factor =
(7‑28)
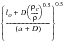
A plot of the notch correction factor against crack size produced by the PCPOST module is shown in
Figure 7‑62.
Figure 7‑62 Plot of Notch Correction Factor Against Crack Size
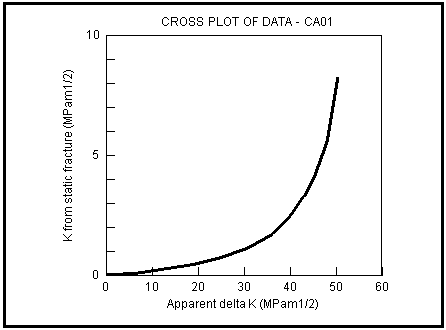
Static Fracture
Fatigue crack growth rate increases with increasing crack size because it is driven by
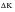
and
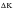
depends on (a)0.5. Nevertheless, as the critical fracture condition is approached, growth rate increases even more rapidly due to the contribution of static fracture modes to the cracking process. Eventually, the crack growth rate becomes infinite (or at least as fast as the speed of sound) when Kmax in the cycle reaches the critical K usually identified with the material fracture toughness.
To model this increase in growth rate from static fracture modes in MSC Fatigue, an additional K, Kfs, is added to Kmax so that
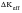
is increased and growth rate is increased according to
(7‑21), the Paris Law. This model (Ref. 20.) is based on LEFM though current research at British Steel is aimed at deriving an equivalent model based on the J integral concept to account for elasto‑plastic fracture modes. The formulas are:
(7‑29)

(7‑30)
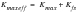
(7‑31)
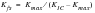
ΔKeff | | Effective 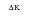 |
Kmaxeff | | Effective maximum K in the cycle |
Kmineff | | Effective minimum K in the cycle |
Kfs | | Additional K from static fracture modes |
Kmax | | Apparent maximum K in the cycle |
KIC | | Material fracture toughness |
Note that Kfs is small at small values of Kmax and tends to infinity as Kmax approaches KIC. The “stat frac” light in the on-line MSC Fatigue display of modifying effects is activated when Kfs is greater than 5% of KIC.
A plot of Kfs with increasing
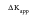
is shown as an illustrative example in
Figure 7‑63.
Cycles Sequence
Under constant amplitude loading, the fatigue crack growth rate response has been modeled using
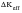
so that crack closure and static fracture are modeled by:
(7‑32)

(7‑33)
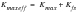
(7‑34)
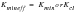
To account for the effect of cycles sequence, the so called “history effect,” an additional term is incorporated into these equations as follows:
(7‑35)
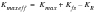
(7‑36)
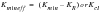
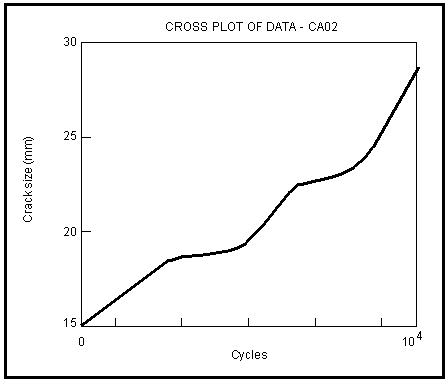
where KR is termed the “residual K.” This residual K arises whenever a previous cycle has produced a crack tip plastic zone that extends beyond the plastic zone of the current cycle. Prior deformation therefore causes the cyclic deformation to deviate from constant amplitude behavior and a history effect results. History effects include retardation (possibly to crack arrest), acceleration, delayed retardation, and what is known as “overshoot” or “lost retardation.” These invalidate linear damage accumulation concepts (Miner’s Rule) and necessitate cycle-by-cycle modeling.
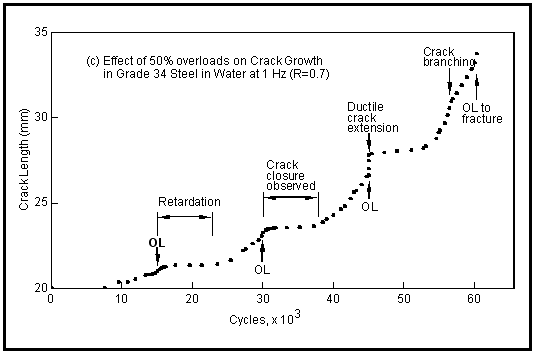
As an example, consider the case of a single overload in a constant amplitude sequence. The crack growing under constant amplitude has two plastic zones associated with its tip: a maximum zone based on Kmax and a reversed zone based on
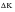
. When the overload occurs, it then has four plastic zones at the crack tip (see
Figure 7‑65) and, because of the confusion and complexity, transient response results. The measured crack size — cycles and growth rate —
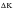
information appears as in
Figure 7‑64 with retardations occurring at each overload.
Figure 7‑64 Crack Length — Cycles Response for Single Overloads
In a random sequence of cycles, the largest current overload governs the response of the crack to each cycle in turn.
The original formulation for KR was due to Willenborg (Ref. 23.)and was subsequently modified by Johnson at NASA (Ref. 24.) at the same time as the closure concepts of Elber (Ref. 25.) were also being introduced to explain and model history effects. The original Willenborg expression was:
(7‑37)
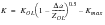
KOL | | K due to the overload |
Δa | | Crack extension since the overload |
ZOL | | Plastic zone size due to the overload and given by: |
(7‑38)
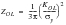
This has been substantially expanded by Austen ((Ref. 13.), (Ref. 14.), (Ref. 20.), (Ref. 21.)) to account for delayed retardation and overshoot as:
(7‑39)
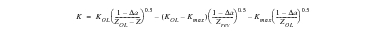
Z | = | Maximum plastic zone size for the current cycle |
Zrev | = | Reversed plastic zone size for the overload |
These are given by:
(7‑40)
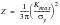
and
(7‑41)
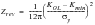
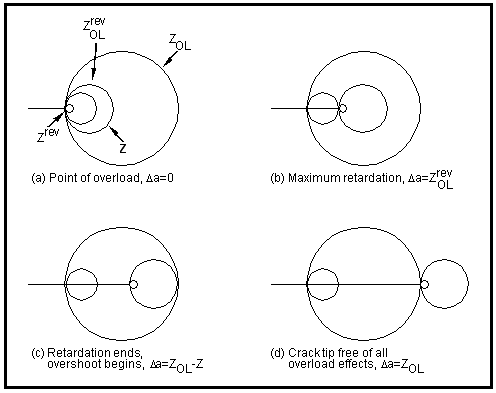
Figure 7‑66 Crack Tip Plastic Zone Interactions Following an Overload
The first term in
(7‑39) describes the decay in KR which becomes zero as the boundary of the current maximum plastic zone crosses that due to the overload as in
Figure 7‑66 (c). The second term in
(7‑39) describes the delayed retardation such that KR is in fact zero at the point of overload (
Figure 7‑66 (a)) and realizes its maximum effect as the moving crack tip crosses the reversed plastic zone due to the overload (
Figure 7‑66 (b)). The third term in
(7‑39) controls the overshoot phenomenon where, during the crack extension phase from
Figure 7‑66 (c) to
Figure 7‑66 (d), KR is negative and increases both Kmaxeff and Kmineff. An overshoot will occur if Kmineff is thus raised above the current closure level, Kcl. During this phase, the crack behaves almost as a closure free short crack and it is only when it is fully clear of the overload zone does “normality” return (
Figure 7‑66 (d)).
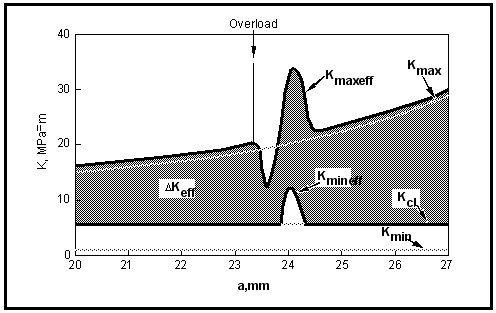
The passage of the crack through the overload zone is illustrated in terms of stress intensity in
Figure 7‑67.
Figure 7‑67 Overload Effects on Stress Intensity
This model not only incorporates delayed retardation, overshoot, and closure but also the significant crack extension caused by an overload is modeled via:
(7‑42)
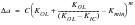
It is notable that in single overload block loading, the growth rate is significantly retarded (which should increase life), but the overall life may in fact be reduced because of premature failure at an overload.
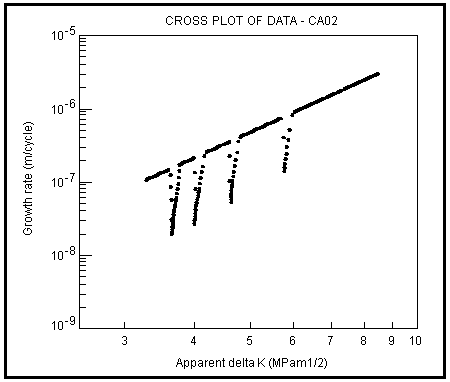
Clearly, history effects are complex but they are physically observed as in the experimental data shown in
Figure 7‑67 and it is only through cycle-by-cycle modeling of the crack tip response that the actual behavior is reproduced in prediction methods and software. In fact,
Figure 7‑64 and
Figure 7‑65 are MSC Fatigue predictions.
Figure 7‑68 Example of Experimental Crack Growth History Showing Sequence Effects (Ref. 21.)
Environment
Fatigue crack growth rates, and hence lifetimes, are strongly influenced by the environment to the extent that corrosion fatigue is a synergistic phenomenon in which corrosion and fatigue are mutually enhanced. Cracks generally adopt that process which gives the fastest rate with the easiest or lowest energy path and this was termed “process competition” in corrosion fatigue modeling (Ref. 15.). To predict lifetimes accurately, environmental influences must be taken into consideration. If materials data is available for the precise environment concerned, then MSC Fatigue can use them for accurate predictions. However, each change of cyclic frequency, waveform, temperature, electrochemical potential or chemical composition of the environment produces a requirement for a new dataset and clearly this is impossible to accommodate within a database even if the test data were available.
The MSC Fatigue module allows materials data for air to be combined with models for the environmental effects on fatigue crack growth rate for the most common environmental mechanism, that of hydrogen embrittlement. In this way, corrosion fatigue can be modeled in the absence of appropriate corrosion fatigue crack growth data for the material/environment system.
In aqueous environments, two electrochemical processes occur: the anodic reaction dissolves metal which makes the crack less sharp, the cathodic process generates hydrogen which, in the presence of cyclic deformation, concentrates in the crack tip plastic zone. Crack tip blunting reduces
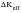
and slows down the growth rate; localized hydrogen embrittlement introduces an alternative, faster growth rate.
The equation which governs the growth rate for local hydrogen embrittlement is:
(7‑43)
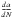
= greater of
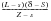
and s
L | | Hydrogen penetration distance = 4(DH•t)0.5 |
s | | Striation width = C (ΔKeff)m |
d | | Maximum crack tip opening F(0.12,σy E) BBC(F(ΔK,(1-R))) 2 |
Z | | Plastic zone size given by (7‑26) |
t | | Cycle rise time |
DH | | Hydrogen diffusion coefficient |
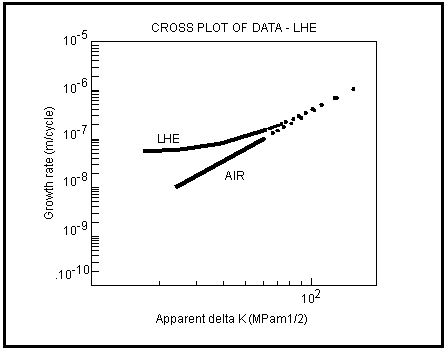
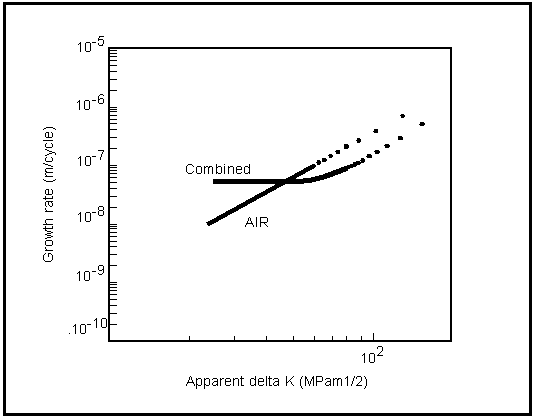
The most important parameter is the hydrogen diffusion coefficient and published values very widely between 10-7 and 10-12 m2/sec. The effect of the hydrogen influence on crack growth rates and life is compared to behavior in air in
Figure 7‑69. In nonaqueous hydrogen bearing environments or if cathodic protection suppresses anodic dissolution in aqueous ones, then only the hydrogen effect needs to be modeled leading to the often observed plateau effect in growth rates (
Figure 7‑69).
Figure 7‑69 Growth Rate Behavior for Local Hydrogen Embrittlement
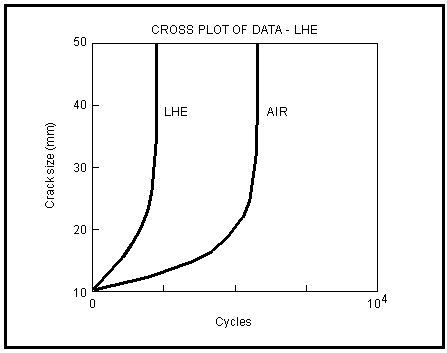
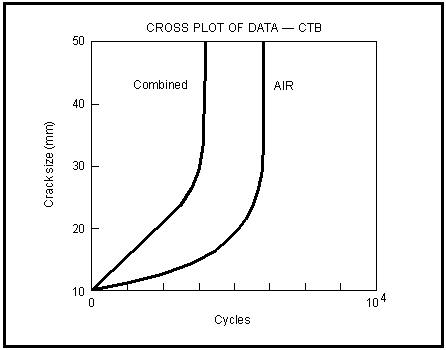
Figure 7‑70 Crack Size — Life Behavior for Local Hydrogen Embrittlement
The blunting effect is accounted for by reduction in
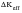
according to:
(7‑44)
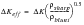
ρsharp | = | Sharp or air crack tip radius |
ρblunt | = | Blunt or corroded crack tip radius |
A full derivation of the derivation of

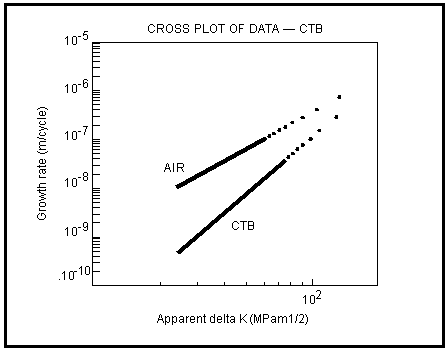
from Faraday’s Laws of electrochemistry is given elsewhere ((Ref. 16.), (Ref. 20.). The most important parameter here is the anodic current density and again, published values vary widely from 10-5 to 1 amp/sq cm. The effect of blunting alone, which may be experienced in square wave loading for example, is shown in comparison to air behavior in
Figure 7‑71 and
Figure 7‑72. The overall combined effect of crack tip blunting and local hydrogen embrittlement is shown in
Figure 7‑73 and
Figure 7‑74.
Figure 7‑71 Growth Rate Behavior for Crack Tip Blunting
Figure 7‑72 Crack Size — Life Behavior for Crack Tip Blunting
Figure 7‑73 Growth Rate Behavior for Combined Corrosion Fatigue Processes
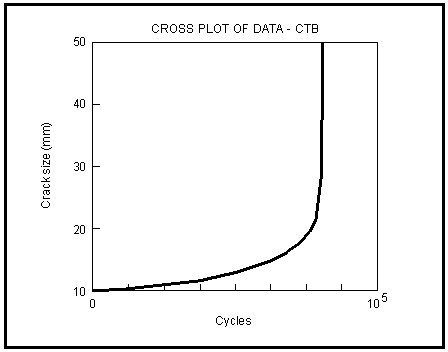
Figure 7‑74 Crack Size — Life Behavior for Combined Corrosion Fatigue Processes
Applications of Fracture Mechanics
There are many potential applications for using MSC Fatigue to solve engineering problems arising from the presence and growth of fatigue cracks. A brief list of some of them is given below:
1. Pre-Prototype Design Analysis — An assessment can be made of the crack tolerance of a design in terms of its safety and integrity throughout its design life. The use of the software predictions may reduce the number of prototype builds by one or more, thus saving considerable time and expense.
2. Prototype Testing — At some stage in the design process, prototype testing may be necessary and the determination of the test program parameters can be enhanced by pre-predicting the test results using MSC Fatigue. Thus, the test program itself can be optimized in terms of time and cost.
3. Inspection Strategy — This is the case where a crack is discovered in a component in service and decisions are required quickly concerning actions to be taken:
• Should the component be removed from service?
• Can it be repaired and returned to service?
• Can it be left until the next planned maintenance?
• If it is safe now, when should it be inspected again?
These questions can be answered using fatigue life calculations and the process repeated at every inspection until a remnant life estimation at the end of the original design life may lead to decisions concerning possible reliving of the component.
4. Failure Analysis — The software can be used to recreate the service failure in the computer, to work backwards to the start point of the known life and reach some conclusions concerning the material, loading, environment and original design and manufacture. The conclusions from the life estimations can be used to determine the probable causes of the failure and to answer questions about the likelihood of similar failures in nominally identical components.
5. Decision Support — MSC Fatigue provides a general set of tools with which to derive evidence to support engineering decisions. Such decisions need not now rely entirely on engineering experience and good sense but can be substantiated by data obtained from “state-of-the-art” life estimation methods.
Estimation of LEFM Data
The parameters required to characterize fracture toughness and fatigue crack growth properties can be generated purely on the basis of ultimate tensile strength, UTS. The rules for this generation are empirical and come from the British Standards Document PD6493 (1991) and the Dynamic Test Agency Structural Integrity Assessment Manual (volume 9, 1994).
The same rules apply for steels, aluminium alloys and titanium alloys for which the values of elastic modulus, E, are assumed to be 210,000, 73,000 and 110,000 MPa respectively. The rules should not be used for other materials.
The parameters are calculated according to the following rules:
(Note that these parameters are in the MPa, MPam1/2 and metres/cycle units system.)
Yield or proof strength, σy: | UTS / 1.3 |
Fracture toughness, KIC: | 0.133 E / σy |
Unnotched fatigue limit, FL: | 0.357 * UTS |
Paris Law coefficient, C: | 92610 / E3 |
Paris Law exponent, m: | 3 |
Threshold at R=0, D0: | 5.38* (E / 210000) |
Threshold at R->1, D1: | 2* (E / 210000) |
Critical R value, Rc: | 0.5 |
da/dN lower threshold: | 1e-11 |
SCC threshold, KISCC: | KIC / 2 |
The above parameters are for non-welded materials in air. If the material is welded then the Paris Law coefficient, C, is increased by a factor of 2. If the material is undergoing fatigue crack growth in an aqueous environment, such as water, then the Paris Law coefficient, C, is increased by a factor of 7.3. If the material is both welded and undergoing fatigue crack growth in an aqueous environment, then the Paris Law coefficient, C, is increased by a factor of 14.6.
Multiaxial Stresses and Crack Propagation Methods
The crack propagation methods incorporated in MSC Fatigue are essentially 1‑dimensional. All geometry, stress-state, and stress distribution information must be taken into account using the stress intensity calibration. The analysis will assume that the crack path, crack shape, and stress distribution (e.g., proportion of tension and bending) are as defined by the stress intensity calibration. MSC Fatigue’s biaxiality indicators provide some means of placing confidence limits on these assumptions.