XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> Introduction
This chapter is dedicated to multiaxial concerns. The stress state in a component and how that stress state changes over time tends to have a great influence on how a crack grows or initiates. The basic fatigue techniques in MSC Fatigue are based on uniaxial stress state assumptions. It is recommended that the user be intimately familiar with these techniques before attempting to solve fatigue problems of structures with multiaxial stress states. The basic uniaxial techniques and usage of the program with these techniques are described in
Using MSC Fatigue (Ch. 2),
Total Life and Crack Initiation (Ch. 5), and
Fatigue Theory (Ch. 15).
Two modules are provided in MSC Fatigue for multiaxial fatigue calculations.
The real difference between the two is that the first uses a multiaxial notch correction procedure to convert purely elastic FE results into elastic-plastic stresses and strains. This is not necessary when dealing directly with measured responses.
For the FE method, it is not recommended to simply use multiaxial techniques immediately without first running a basic analysis based on uniaxial assumptions along with a multiaxial assessment by running a biaxiality analysis. A multiaxial analysis of an entire model can be a computationally intensive operation and thus should only be resorted to if necessary and then again, only for the critical locations of a model.
MSC Fatigue allows the user, during a basic fatigue analysis, to do a biaxiality analysis. This is described in
Using MSC Fatigue (Ch. 2) in detail. To summarize here, a biaxiality analysis will give you a good understanding of the stress state in your model and how that stress state varies with time. It uses surface resolved stresses (the state of stress on the surface of the model must be plane stress meaning the out-of-plane stress,
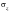
, must be zero). It then uses the two in-plane principal stresses to determine the biaxiality ratio,
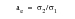
, where
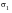
is the absolute maximum in-plane principal stress and
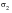
is the other in-plane principal. This parameter can take on values between minus one (pure shear) and plus one (fully biaxial).
A biaxiality analysis also will determine the standard deviation of the biaxiality ratio and the angle spread, that is, how the biaxiality ratio is changing over time and whether or not the angle,

, that
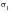
makes with the local x-axis is changing. With these three parameters the stress state can be determined using the following guidelines:
Value of ae | Value of f | Stress State |
0 | Constant | Uniaxial |
-1<=ae<=+1
Constant but not zero | Constant | Proportional Loading |
Varies | Varies | Non-proportional Loading |
Uniaxial stress states can be fully handled by the basic techniques of MSC Fatigue as previously stated.
Proportional loading means that you no longer have a uniaxial stress state but that the relative magnitude of
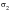
to
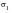
is not changing with time, i.e. they remain proportional to each other. This case can also be fully handled with the basic techniques of MSC Fatigue by setting the biaxiality correction on and possibly using a signed tresca shear stress parameter as opposed to using the default maximum absolute principal.
Only when the third state of the above table actually exists (non-proportional loading) do the techniques described in this chapter need to be resorted to. To summarize the approach to assess for multiaxiality:
1. Calculate surface resolved stresses. For shell elements this is normally not necessary in that the stresses are already surface resolved. For solid elements this can be done using the
Calculate Normals, 71 option. Also see the discussion below in
2. Run a global crack initiation or S-N fatigue analysis using the basic methods with the biaxiality analysis turned on to determine the fatigue critical locations and to calculate the multiaxial assessment parameters such as
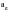
.
3. Use the post-processing techniques in MSC Patran or MSC Fatigue Pre & Post to evaluate the mean biaxiality ratio, standard deviation of the mean biaxiality ratio, and the angle spread at the critical locations of the model as previously described. Cross plots of the stress parameter versus these multiaxial assessment parameters can also be created at critical locations over the entire time series to help with the assessment.
4. If uniaxial conditions exist, no further steps are necessary.
5. If a proportional loading state exists in the critical locations, correct by turning on the biaxiality correction using the basic analysis.
6. If a non-proportional loading exists in the critical locations, you must resort to the techniques described in this chapter.
Surface Resolved Stresses from FE Models
Many of the multiaxial models used in the module FEMLF are applicable on free surfaces only; in fact all do except the Dang Van model, which does not care. These models require surface resolved stresses and 2-D stress states. When working with shell models, this is not a problem because the stresses are normally already plane stress in a surface resolved coordinate system, with zz, xz and yz stress components being zero. The problem arises when dealing with solid models, where the stresses are surface resolved, but in general, due to the errors in the finite element model, especially in extrapolating stresses to the free surface, the zz, xz and yz stress components will not be zero. There are various possible strategies for dealing with this issue.
1. The first option, and this is the one currently being used, is to ignore the zz, yz and zx stresses. This method has the advantage of simplicity, and is of course correct if the stresses really are 2D. However, in a FE solid model, you would generally expect the displacements of the surface nodes and hence the surface strains to be calculated relatively accurately, and the surface stresses to be less accurate, due to the inaccuracy in extrapolation to the surface. If you calculate the surface strains from the stresses, the accuracy of these will also be compromised.
2. The second option is, when calculating stresses and strains on any plane, always to consider the whole stress tensor. Because the stresses are in any case calculated by the FE from the strains, this approach should give accurate values of the in-plane strains. However, the stresses, and also the out-of-plane strains will have errors due to the non-zero surface normal components, which cannot be present in practice.
3. The third option is to use the whole stress tensor to calculate the in-plane strains, and this will give the same strain values as predicted by the original FE calculation.
(6‑1)
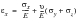
(6‑2)
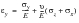
(6‑3)

The surface normal strain and direct in-plane stresses could then be recalculated from Hooke's law assuming all the components containing z are zero, thus:
(6‑4)
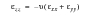
(6‑5)
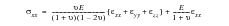
(6‑6)
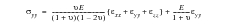
(6‑7)
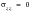
This is generally the best method, because:
1. The in-plane strains are always correct.
2. The surface normal stress is zero.
3. The stresses and strains are consistent with one another.
See
Multiaxial Low Cycle Fatigue Analysis, 473 in the Theory section for more details.