XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> Crack Initiation/Strain-Life (ε‑N) Analysis
The nominal stress approach has been used extensively in the study of premature failures of components subjected to fluctuating loads. Traditionally, the magnitude of the observed cyclic stresses were observed to be less than the tensile elastic limit and the lives long (i.e., greater than about 10 5 cycles). This pattern of behavior has become known as high-cycle fatigue.
As duty cycles have became more severe and components more complicated, another pattern of fatigue behavior has emerged. In this regime, the cyclic loads are relatively large and have significant amounts of plastic deformation associated with them together with relatively short lives. This type of behavior has been commonly referred to as low-cycle fatigue or more recently strain-controlled fatigue. The transition from low-cycle to high-cycle fatigue behavior generally occurs in the range 10 4 to 10 5 cycles. A more precise definition of this transition will be developed later.
The analytical procedure evolved to deal with strain-controlled fatigue is called the strain-life, local stress-strain or critical location approach. In MSC.Fatigue, it is referred to as the crack initiation method for reasons that will become clear later.
The Microscopic Aspects of Fatigue Failure
It is almost universally agreed that fatigue failures usually start at the surface of a fatigue specimen or component. This is true whether the test is made in a rotating‑beam machine where the maximum stress is always at the surface, or in a push‑pull machine which gives a simple tensile-compressive stress cycle. Furthermore, fatigue failures start as microscopic cracks and accordingly are very sensitive to even minute stress raisers. It is quite apparent from these considerations, that a fatigue specimen will give results which are representative of the metal tested only if its surface is free of defects. Tool or grinding marks left on the surface make the formation of fatigue cracks easier and may result in low apparent values of fatigue limit or strength.
Early research into the mechanisms of fatigue clearly demonstrated that the failure process is linked to reversed plastic flow (i.e., the forward and backward motions of dislocations). (Dislocations are imperfections in the crystal lattice of a metal and are responsible for nearly all aspects of plastic deformation along the slip planes of metallic crystals.) Under cyclic loading, the direction of the strain is reversed over and over again; the slip lines that appear on the surface reflect this fact.
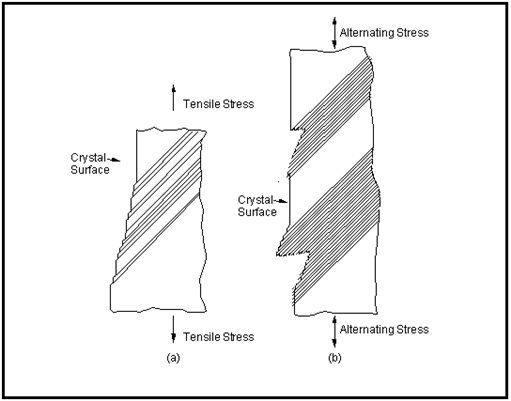
When the strain is monotonic, the slip steps that appear on a crystal surface have a relatively simple topology, see
Figure 15‑25(a). On the other hand, under cyclic loading, the slip bands tend to group into packets or striations. The surface topology of these striations is more complex and is indicated schematically in
Figure 15‑25(b). Note that both ridges and crevices tend to be formed. There is good evidence that the crevices are closely associated with the initiation of cracks. Whether or not crevices are formed in a particular specimen or a specific grain of a particular specimen is largely a function of the crystal orientation. If the shear direction in the striation is nearly normal to the surface, crevice formation will be favored. However, if the slip direction is parallel to the surface, crevices are not normally formed. It is possible, even in this case, for damage to occur inside a striation, since pores or holes can also open up inside the slip-band packet.
A further consequence of these repeated dislocation movements is that small localized deformations called
extrusions may occur in the slip bands. An extrusion is a small ribbon of material which is apparently squeezed out from the surface of a slip band. The inverse of extrusions, which are narrow crevices called
intrusions have also been observed,
Figure 15‑25(b). Typically these surface disturbances are approximately 1 to 10 microns in height and constitute embryonic cracks.
Figure 15‑25 Surface Contours Where Slip Bands Intersect a Surface
Another way of describing the above observations is that without some plastic deformation there can be no fatigue damage! Given this assertion, how could it be that the nominal stress approach, which specifically overlooks plasticity, could have been so successfully applied for so many years?
The reason is that, in the high-cycle regime loading, levels are low and so stress and strain are almost linearly related. Under these circumstances, load and strain‑controlled cycling are equivalent. Consequently, in the area of the endurance limit, load-controlled rotating beam fatigue data based on notionally elastic nominal stresses can be used to describe adequately fatigue behavior. However, as the load levels become larger, the method breaks down and a more generalized, strain-based approach, which accounts for plasticity, must be adopted. Indeed, it should be clear by now that the nominal stress approach is in reality a special case of strain-based analysis, as the plastic strain tends to zero.
Figure 15‑26 Similitude Between a Laboratory Specimen and the Root of a Notch
The Strain-Life Methodology
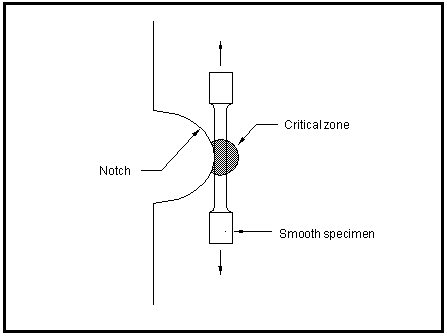
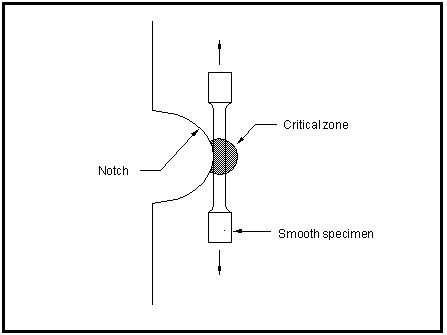
The strain-life methodology is based on the observation that in many critical locations such as notches the material response to cyclic loading is strain rather than load controlled. This arises from the fact that whilst most components are designed to confine nominal stresses to the elastic region, stress concentrations such as notches often cause plastic deformation to occur locally. The material surrounding the plastically deformed zone remains fully elastic and so the deformation at the notch root is considered to be strain controlled.
The strain-life method assumes similitude between the material in a smooth specimen tested under strain control and the material at the root of a notch
Figure 15‑26. For a given loading sequence, the fatigue damage in the specimen and the notch root are considered to be similar and so their lives will also be similar.
The cyclic stress-strain response of the material at the critical location is determined by characterizing the behavior of smooth specimens subjected to similar loading, the local stress-strain history. The local stress-strain history must be determined, either by analytical or experimental means. Stress analysis procedures such as finite element modelling, or experimental strain measurements are usually required.
In performing smooth specimen tests which characterize fatigue performance, it must be recognized that fundamental material properties are being measured which are independent of component geometry. Phenomena such as cyclic hardening or softening, cycle dependent stress relaxation, and loading sequence effects are all taken into consideration.
Monotonic Stress-Strain Behavior
The engineering tension test is widely used to provide basic information on the strength of materials and also as an acceptance test for the specification of alloys. In this test, a cylindrical specimen is subjected to a continually rising, monotonic, uniaxial load while simultaneously measuring its elongation.
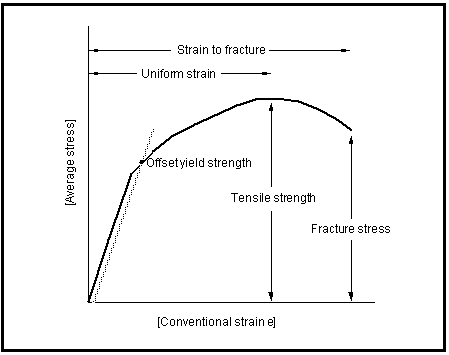
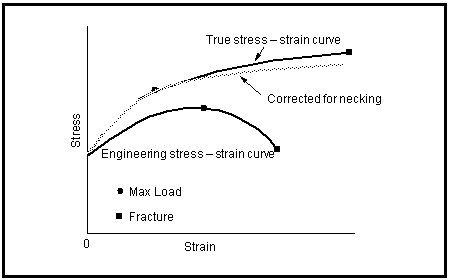
The so-called engineering stress-strain curve can be constructed from the measured values of load and elongation,
Figure 15‑27.
The stress plotted on the engineering stress-strain curve is the average longitudinal stress in the test specimen and is obtained from:
(15‑40)
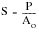
S | | the nominal or engineering stress |
P | | the applied load |
Ao | | the original, unloaded, cross-sectional area |
Figure 15‑27 The Engineering Stress-Strain Curve
The engineering strain is the average linear strain obtained from:
(15‑41)
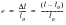
e | | the engineering strain |
lo | | the unstrained specimen gauge length |
l | | the strained gauge length |
The shape and magnitude of the engineering stress-strain curve goes a long way towards characterizing any particular material. The curve itself may be considered to be made up of three distinct regions. Uniform straining where stress and strain are linearly related, uniform straining where stress and strain are no longer linearly related, and a nonuniformly straining region where plastic instability, necking, sets in.
Certain parameters may be measured directly from the engineering stress strain curve. For example, yield strength, tensile strength, percentage elongation, and reduction in area.
The yield stress is used to define the limit of elastic behavior. In some steels, it may be easily defined as a sharp transition between elastic and elastic-plastic behavior. More commonly, it is defined, as in
Figure 15‑27, by a fixed offset (i.e., the stress corresponding to 0.2% plastic strain for example):
(15‑42)
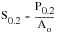
The tensile strength, sometimes referred to as the ultimate tensile strength (UTS or Rm), corresponds to the stress resulting from the maximum load carried by the specimen. It is calculated by dividing the maximum load by the original cross‑sectional area of the specimen:
(15‑43)
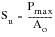
The tensile strength defines the limit of uniform plastic deformation within the tensile test. It is not actually a fundamental material property, but rather it is a function of the test itself. However, it has been and remains the most widely quoted material property, indeed entire national standards are based around it.
Both percentage elongation and reduction in area are measures of ductility, that is the extent to which a metal will deform prior to fracture. Typically, these properties are measured by putting a fractured tensile specimen back together and measuring its final length, lf, and final area, Af thence:
Percent elongation, EL% = (lf - lo) / lo x 100
Percent reduction in area, RA% = (Ao - Af) / Ao x 100
True Stress and Strain
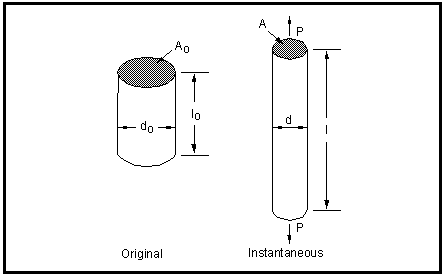
All the parameters derived above have been based on the original dimensions of the test specimen, and as such are normally referred to as engineering stress and strain parameters and denoted by S and e respectively. A true stress is defined as the load divided by the instantaneous area, P / A, and since the specimen is stretching and its cross-sectional area decreasing, the true stress is always larger than the engineering stress.
Up to the onset of necking, a true strain is based on instantaneous gauge length, and is defined as the integral from the original length, lo, to the instantaneous length l, of 1 / l, otherwise:
(15‑44)
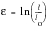
Figure 15‑28 Original and Instantaneous Specimen Geometries
When engineering stress and strain are corrected to their true values and the data replotted, the nature of the stress strain diagram changes,
Figure 15‑29. True stress and strain may be related to engineering stress and strain (i.e., true stress, up to necking).
(15‑45)
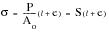
S | | the engineering stress |
e | | the engineering strain |
Figure 15‑29 True Stress/True Strain Diagram
Beyond necking, true stress must be calculated from actual measurements of load and instantaneous cross-sectional area from:
(15‑46)
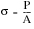
True strain, up to necking:
(15‑47)
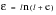
Beyond necking, true strain can be calculated from:
(15‑48)
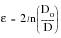
Do | | the original diameter |
D | | the instantaneous diameter |
The fracture stress corresponds to the highest stress carried by the specimen and is calculated by dividing the fracture load, Pf, by the final area, Af.
Stress-Strain Relationships
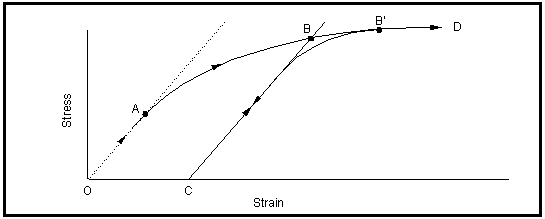
Figure 15‑30 below illustrates various regions of a true stress/true strain curve. The curve has been generated by monotonically loading a specimen up to point B and then unloading down to point C and then reapplying the load up point D.
The portion of the curve defined by O-A represents the elastic, reversible, behavior of the material where stress and strain are linearly related.
Figure 15‑30 Various Regions of the True Stress/True Strain Curve
The constant of proportionality is called the modulus of elasticity or sometimes the stiffness. In this region:
(15‑49)
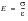
and any elastic strain,
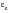
may be written as:
(15‑50)
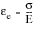
The region B-D defines the elastic-plastic part of the true stress/true strain curve, and for most metallic materials, this region can be represented by a simple power law of the form:
(15‑51)
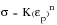
K | | the constant of proportionality is known as the strength coefficient. |
n | | known as the work hardening coefficient. |
| | the plastic strain. |
The plastic strain,
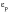
, can now be written as:
(15‑52)
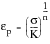
Reversing the Loading Direction
If during the course of a monotonic tension test, point B in
Figure 15‑30 for example, the loading direction is reversed and the specimen unloaded, the stress-strain relationship will follow the line defined by B-C. The slope to the line will be the same as O-A, that is to say, equivalent to the modulus of elasticity, E. Indeed, this is the most accurate way of measuring E during the course of a tension test.
The distance O-C represents a permanent extension of the specimen as a result of loading it up to point B. This extension, the plastic strain, is sometimes referred to as the permanent set.
The distance C-C' represents the recoverable extension of the specimen as a result of loading it up to point B, and is known as the elastic strain.
The total strain induced into the specimen by loading it up to point B, therefore, is the sum of the elastic and plastic components:
(15‑53)
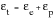
and utilizing the expressions derived above the total strain can be written as:
(15‑54)
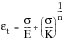
which represents a good description of the true stress/true strain curve.
At fracture, point D in
Figure 15‑30, two further parameters can be defined — the
true fracture strength and the
true fracture ductility. True fracture strength,
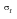
, is the true stress at final fracture and is defined as:
(15‑55)
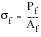
The true fracture ductility,
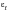
, is the true strain at final fracture and is defined in terms of the initial area and the area at fracture:
(15‑56)
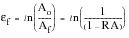
where the reduction in area RA is defined as:
(15‑57)
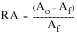
Reversing the Loading Direction, Again
If, from point C in
Figure 15‑30 above, the loading direction is again reversed (i.e., the specimen is loaded back towards point B and beyond), the true stress/true strain curve will follow the trace C-B'-D. As in the case of unloading, most of the trace will be a straight line with slope equal to the modulus of elasticity, E. The interesting thing to note, however, is that the new stress-strain curve C-B'-D rejoins the original stress-strain curve at B'. It is almost as though the material remembered the nature of the original curve and continued to deform along it. Conversely, once beyond B' the material has apparently totally forgotten the excursion B-C-B' and goes on to fracture at D as though it had never happened! The excursion B-C-B' is, therefore, only an interruption in the primary loading process O-A-B-D, and in reality, represents a fatigue cycle. These observations are central to the local strain life methodology and we shall return to them later.
The Bauschinger Effect
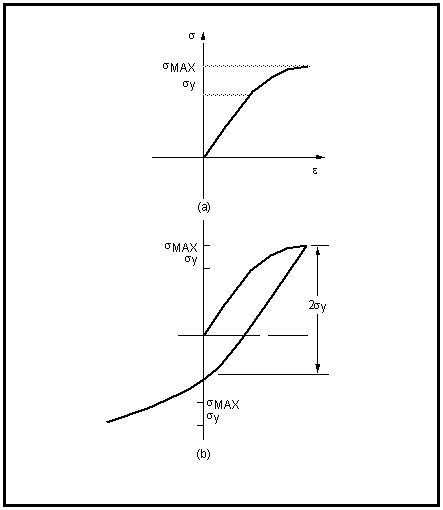
Since 1886, Bauschinger was carrying out and reporting experiments of the sort described above. In reality, he went further in that he did not stop the unloading process at the zero stress level, point C in
Figure 15‑30, but rather continued on down into full compression.
Figure 15‑31 illustrates what he found.
In
Figure 15‑31(a), a specimen of material is loaded in tension to beyond the yield stress to a maximum stress of
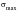
, point A. At this point the loading direction is reversed and the specimen is unloaded from point A through the zero stress level and on into compression to a stress equal to
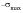
, point B. The interesting point to note is that the material appears to yield at a stress level before
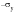
is reached (
Figure 15‑31(b)). This observation has nothing to do with the fact that the yield strength in compression might be different from that in tension. The whole experiment could be repeated, but this time loading in compression first by going to
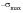
. Yield would take place at
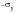
but would again occur before
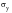
was reached when the loading direction was reversed. Unsurprisingly, this behavior is known as the Bauschinger effect and its importance cannot be overstated.
Figure 15‑31 Reversed Loading Into Compression, the Bauschinger Effect
At this point, a valid question to ask would be: If reversed yield does not take place at
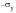
, then at what point does it take place?
Figure 15‑31(b) provides the necessary clue (i.e., at a stress level equal to 2
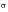
y from
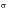
max). It appears as though the stress‑strain curve defined by A-B is geometrically twice the initial true stress/true strain curve O-A. This observation was first made by Masing, in 1926, and is today known as Massing’s hypothesis.
Cyclic Stress-Strain Behavior
If the loading process started in
Figure 15‑31 is continued and at
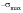
, the loading direction is again reversed and the specimen is loaded back up to
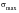
, then a complete loop will be defined (see
Figure 15‑32). The stress-strain loop illustrated in
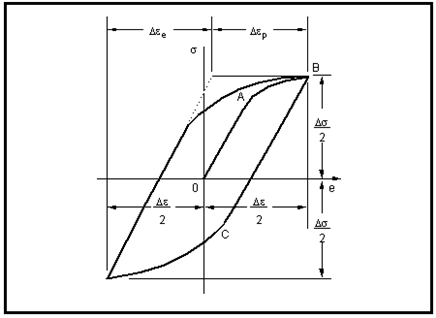
Figure 15‑32 is called a hysteresis loop and defines, in stress-strain space, a single fatigue cycle. Typically such loops are generated in the laboratory under strain control; that is, by straining to specific strain limits. During the initial loading, the stress-strain response is according to the curve O-A-B.
Figure 15‑32 A Complete Stress-Strain Cycle, a Hysteresis Loop
On unloading, yielding begins in compression at point C due to the Bauschinger effect. In reloading, in tension the hysteresis loop develops. The dimensions of the loop are described by its total width, the total strain range
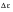
, and its height, the total stress range
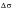
.
The total strain range is made up of the elastic and plastic components:
(15‑58)
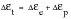
which may be written as:
(15‑59)
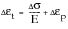
Cyclic Loading Under Strain Control
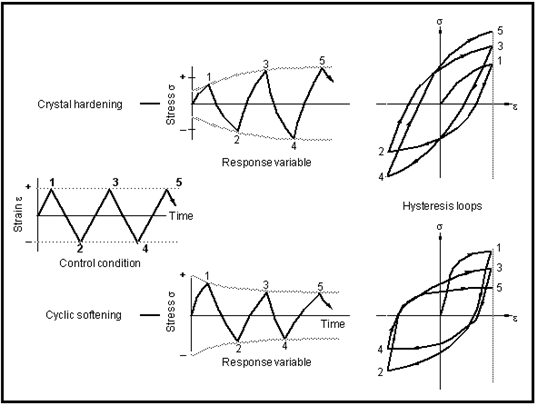
If a material is repeatedly cycled between fixed strain limits one of several things may happen depending on its nature and initial conditions of heat treatment.
Figure 15‑33 Cyclic Hardening and Softening Under Strain Control
The material could respond in any one of the following ways,
• it could cyclically harden
• it could cyclically soften
• it could remain stable
• it could soften or harden depending on strain range
Figure 15‑33 illustrates the effects of cyclic softening and hardening where the first two hysteresis loops of two different materials are plotted. In both cases, the cycling of the specimen is between fixed-strain limits and the load is allowed to find its own level. It is clear that in the case of hardening, the maximum stress reached in each successive strain cycle increases with number of cycles and in the case of softening the maximum stress decreases with number of imposed cycles. This process does not continue indefinitely. In both cases, the stress will find a constant level and remain stable at that level until the first emergence of a fatigue crack.
The reason materials cyclically harden or soften is thought to be associated with dislocation substructures within the metal crystal lattice. Broadly speaking, soft materials such as aluminium, which contain low dislocation densities, tend to harden; whereas, hard materials, such as steels, tend to soften. As a rule of thumb, the ratio of the ultimate tensile strength, Su to the 0.2% proof strength, S0.2 can be used to gauge whether a particular material will cyclically harden or soften, if
(15‑60)
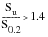
(15‑61)
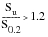
For ratios between 1.2 and 1.4, the estimate is difficult and anything may happen — hardening, softening or both.
Determining the Cyclic Stress-Strain Curve
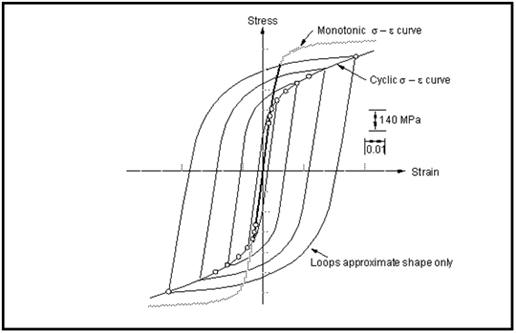
As mentioned above, under strain control and early in life, the stress-strain response of most materials changes significantly with applied cyclic strains. However, after a relatively small number of cycles, typically no more than about 10% of total life, the hysteresis loops tend to stabilize so that the stress amplitude remains reasonably constant over the remaining portion of fatigue life. If the stress, strain coordinates of the tips from a number of stable hysteresis loops, of differing strain amplitudes, are plotted in stress-strain space, then the locus of these points defines the cyclic stress-strain curve, see
Figure 15‑34.
Figure 15‑34 Definition of the Stable Cyclic Stress-Strain Curve
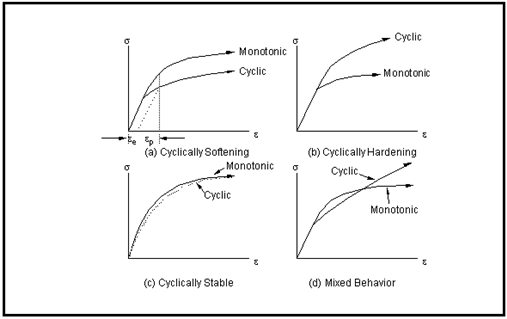
Figure 15‑35 Comparison Between Cyclic and Monotonic Stress-Strain Curves
The cyclic stress-strain curve defines the relationship between stress and strain under cyclic loading conditions, just as the tensile true stress/true strain curve defines the conditions under monotonic loading. The cyclic stress-strain curve can be compared directly with the monotonic stress-strain curve to quantitatively assess the cyclically induced changes in material behavior.
Note that, in
Figure 15‑35(a), when a material cyclically softens the cyclic yield strength is considerably lower than the monotonic value. Using monotonic properties in cyclic applications can result in the prediction of fully-elastic strains when in reality considerable plastic strains are being generated.
It is also interesting to note that whilst stabilization of hysteresis loops can consume 10‑20% of total life in a constant amplitude test, a single large overload in service can produce an immediate change from the monotonic curve to the cyclic. It is a sobering thought that the assembly of or using a machine or component could cause an instant reduction of yield strength of up to 50%.
Figure 15‑35(d) illustrates a common behavior for low strength steels, whereby the material both hardens and softens depending on the strain amplitude. This phenomena is often known as mixed mode behavior.
As with the monotonic stress-strain curve, the cyclic stress-strain curve consists of both elastic and plastic strains:
(15‑62)
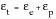
and can be fully characterized by an expression equivalent to that developed for the monotonic stress-strain curve. However, in this case, primes appended to the values of n and K to distinguish them from their monotonic counterparts:
(15‑63)
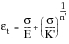
K' | | called the cyclic strength coefficient. |
n' | | called the cyclic strain hardening exponent. |
Typically, K' takes values in the range 1000 to 3000 MPa and n' varies between about 0.1 to 0.2. In general, metals with a high monotonic strain hardening exponent, n, will harden whilst those with a low monotonic strain hardening exponent will cyclically soften.
Table 15‑10 compares the cyclic stress-strain behavior of a number of well-known alloys.
Table 15‑10 Material | Heat Treatment | 0.2% Yield mono/cyclic | n/n’ mono⁄cyclic | Cyclic Behavior |
OFHCCopper | Annealed Partial anneal Cold worked | 20/138 255/200 345/235 | 0.40/0.15 0.13/0.16 0.10/0.12 | Hardens Stable Softens |
|
|
|
Aluminium Alloys 2024 7075 | T4 T6 | 305/450 470/520 | 0.20/0.11 0.11/0.11 | Hardens Hardens |
|
|
Titanium Alloy Ti-8A1-1Mo-1 | Annealed | 1000/790 | 0.078/0.14 | Mixed |
|
Steels SAE4340 SAE 1045 | Q+T 1206 UTS Q+T 2050 UTS Q+T 1725 UTS Q+T 1550 UTS Q+T 1345 UTS | 1170/760 1860/1720 1690/1275 1517/965 1275/758 | 0.066/0.14 0.071/0.14 0.047/0.12 0.041/0.15 0.044/0.17 | Softens Stable Softens Softens Softens |
|
|
|
|
|
SAE 4142 | Q+T 1930 UTS Q+T 1640 UTS Q+T 1550 UTS Q+T 1310 UTS | 1690/1725 1725/1345 1585/1070 1380/825 | 0.092/0.13 0.048/0.12 0.04/0.17 0.051/0.18 | Stable Softens Softens Softens |
|
|
|
Cyclic Yield and the Fatigue Limit
The close association between plasticity and fatigue damage has already been mentioned. This point can be further illustrated through a consideration of the cyclic stress-strain properties of some typical steels, see
Table 15‑11.
Table 15‑11 Monotonic Properties |
Material Low strength Medium strength High strength | Yield Stress
(MPa) 350 650 1090 | Ultimate Tensile Stress
(MPa) 540 790 1160 |
|
|
|
Cyclic Properties |
Material Low strength Medium strength High strength | Strength coefficient
K’, MPa 1340 1062 1620 | Hardening exponent
n’ 0.226 0.123 0.112 |
|
|
|
From the cyclic properties, it is possible to use the equation for the cyclic stress‑strain curve,
(15‑64)
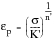
(15‑65)
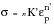
to calculate say the 0.02% cyclic yield stress (i.e., the stress corresponding to 0.02% plastic strain). Note that this is
one tenth the amount of plastic strain usually used to determine an offset yield stress. Broadly speaking, this stress represents a limit below which the level of plasticity is sufficiently low to ensure little or no fatigue damage (i.e., a
fatigue limit). Values of the calculated cyclic yield together with the ratio of cyclic yield to ultimate tensile strength are tabulated below for the three steels, see
Table 15‑12.
Table 15‑12 Material | Cyclic Yield (MPa) | Cyclic Yield / UTS |
Low strength Medium strength High strength | 195 372 624 | 0.36 0.47 0.53 |
|
|
It is interesting to note that the ratios of cyclic yield to UTS are in the region of 0.5. This is consistent with the observation from the nominal stress approach that the endurance limit for steels is about one half the UTS and also supports the view that endurance limit and cyclic yield are closely related if not the same.
Hysteresis Loop Shape
Massing’s hypothesis states that the limb of a stress-strain hysteresis loop is geometrically similar to the cyclic stress strain curve but numerically twice it. Consequently, the equation for the limb can be derived directly from the equation of the cyclic stress-strain curve.
Consider any point on the cyclic stress-strain curve with coordinates
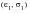
, it follows that:
(15‑66)
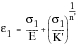
From Massing’s hypothesis, the same point can be located on the hysteresis loop curve and it will have coordinates
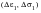
where:
(15‑67)
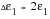
(15‑68)
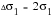
Substituting into the equation for the cyclic stress-strain curve:
(15‑69)
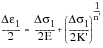
which in the general case reduces to:
(15‑70)
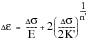
The relationship between the cyclic stress-strain curve and hysteresis loop shape is illustrated in more detail in the following example.
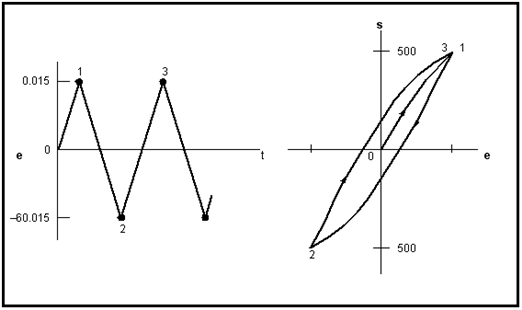
Example 4: Calculating Cyclic Stress-Strain Response
A test piece with the following cyclic properties,
cyclic strength coefficient, | K' = 1200 MPa |
cyclic strain hardening exponent, | n' = 0.2 |
modulus of elasticity, | E = 210,000 MPa |
is to be cycled under strain control with a fully-reversed strain range of 0.03. Calculate the expected stress-strain response.
In calculating the stress-strain response, it will be necessary to make two assumptions.
Firstly, it will be assumed that the material will follow the cyclic stress-strain response rather than the monotonic one on initial loading from zero to the maximum strain amplitude of 0.015. While there is a case for the use of the monotonic response for the first half cycle, in practice after repeated loading, the resulting hysteresis loop tip always migrates towards the cyclic stress-strain curve.
Secondly, it will be assumed that the material will exhibit cyclically stable response from the initial loading. A more precise analysis would require accounting for the cyclic hardening or softening characteristics of the material. As in the case of the first assumption above, the cyclic modelling process is used to model the stable hysteresis behavior since in most cases this occupies the majority of fatigue life.
Figure 15‑36 (a) illustrates a portion of the strain time sequence that is to be used to cycle the test specimen. The value of the stress corresponding to the first turning point, 1, can be calculated directly from the equation for the cyclic stress-strain curve,
Figure 15‑36 (a) The Driving Strain History. (b) The Stress-Strain Response
The value of
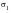
can be calculated from the above equation by using an iterative technique such as Newton Ralphson or interval halving. Such a procedure will provide a value of
The value of the stress at the next turning point, 2 (in
Figure 15‑36 (a)), can be calculated by considering the total strain range, 0.03, together with the equation for twice the cyclic stress-strain curve,
Solving this equation by iteration leads to a value of
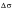
= 1000 MPa. The coordinates of the second turning point in stress-strain space can now be calculated from:
The coordinates of the third turning point can be calculated in the same way as for the second point, and for the fully reversed loading being considered here, they must be the same as for the first turning point.
Figure 15‑36 (b) illustrates the stress‑strain hysteresis loop corresponding to the induced cyclic loading.
The Strain-Life Curve
A number of years ago, Basquin observed that stress-life data may be represented by a straight line relationship when plotted using log scales. The relationship could be expressed in terms of true stress as:
(15‑71)
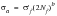
| | the true cyclic stress amplitude |
| | the regression intercept called fatigue strength coefficient |
2Nf | | number of half cycles, reversals, to failure |
b | | the regression slope called the fatigue strength exponent |
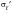
and b are considered to be material properties with the fatigue strength coefficient being approximately equal to the monotonic fracture stress,
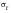
, and b varies between -0.05 and -0.12.
The Basquin equation may be rewritten in terms of elastic strain amplitude:
(15‑72)
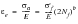
| | the elastic strain amplitude |
E | | the modulus of elasticity |
In the 1950s, Coffin and Manson independently proposed that the plastic strain component of a fatigue cycle may also be related to life by a simple power law:
(15‑73)
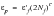
| | the plastic strain amplitude |
| | the regression intercept called fatigue ductility coefficient |
2Nf | | number of half cycles, reversals, to failure |
c | | the regression slope called the fatigue ductility exponent |
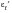
and c are considered to be material properties with the fatigue ductility coefficient being approximately equal to the monotonic fracture strain,
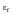
, and c varies between -0.5 and -0.8. More recent work, notably by Morrow, has indicated that the total strain amplitude, that is the sum of the elastic and plastic components, may be better correlated to life.
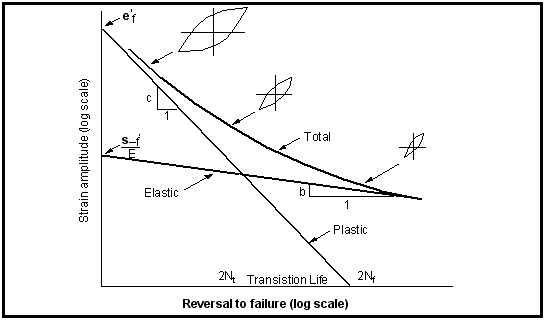
Figure 15‑37 illustrates schematically the nature of the total strain-life curve.
Figure 15‑37 The Total Strain-Life Curve
Mathematically, this curve can be described by summing together the Basquin and the Coffin-Manson component curves:
(15‑74)
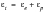
(15‑75)
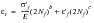
Note that there is no fatigue limit defined by this equation and so it is usual to define a cutoff in terms of reversals which specifies an endurance limit. Typically, the cutoff is set to about 5 x 107 reversals.
Strain-Life vs. Stress-Life
In the realm of high-cycle fatigue, the equation for the S-N curve is usually written as:
(15‑76)
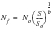
which may be rearranged as
(15‑77)
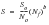
and at one cycle So is the intercept between the S-N line and the stress axis, approximately, the fracture stress, Sf and so
(15‑78)
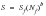
The Basquin equation may be rearranged so that:
(15‑79)
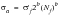
It is clear that these two equations are the same, particularly since magnitude of b is about -0.1 and 2b is close to unity. The thing to note from this comparison is that the classical S-N curve is actually a subset of the total strain-life curve and also that the fundamental material S-N curve, as opposed to a component S-N curve, can be derived from the low-cycle fatigue parameters,
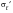
and b. It is important to remember that whilst the elastic S-N curve is defined all the way up to,
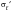
, it should only be used within the high-cycle regime (i.e., above the
transition life).
Transition Life
In
Figure 15‑37, the point where the plastic and elastic life lines intersect is called the
transition life. The transition life represents the point at which a stable hysteresis loop has equal elastic and plastic components. At lives less than the transition, plastic events dominate elastic ones and at lives longer than the transition elastic events dominate plastic ones. From this point of view, therefore, the transition life represents a very convenient and important way of delineating between the low‑ and high-cycle fatigue regimes.
This distinction is important because the solutions which may be proposed to a particular fatigue problem depend entirely on the dominant loading regime. Problems of high-cycle fatigue are usually tackled through the selection of stronger, higher UTS, materials, or through the application of compressive surface stresses through shot peening or nitriding, etc. These solutions would be largely ineffective for the treatment of a low-cycle fatigue problem. Indeed, the selection of a material with a higher UTS, and presumably a lower ductility, could make the situation worse.
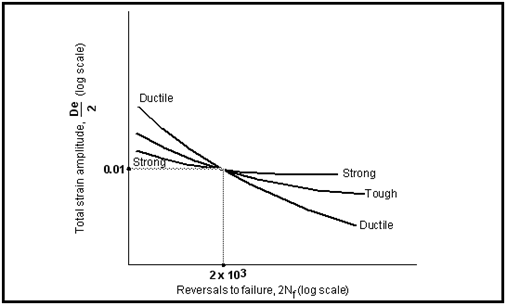
Figure 15‑38 Idealized Representation of Several Strain-Life Curves
These observations are further emphasized in
Figure 15‑38 where three idealized materials are shown, one very high strength material (strong), one ductile material (ductile), and one whose properties lie between the two extremes (tough). The curve cross at about 2 x 103 reversals, 1000 cycles, at a strain amplitude of about 0.01. Thus, one would select the “strong” material for a design life requirement greater than 1000 cycles, pick the “ductile” material for design life requirements shorter than 1000 cycles, and “optimize” with the “tough” material for spectrum loading of a more complicated nature. It is interesting to note that all types of ductile materials seem to have about the same fatigue resistance for a strain amplitude of about 0.01, corresponding to a failure life of about 1000 cycles.
The transition life can be derived directly from the equation of the strain-life curve. At the transition, the elastic and plastic strain amplitudes are equal so that at Nf = Nt
and
Example 5: Transition Life and Shot Peening
A component is manufactured from a steel with the following cyclic properties:
fatigue strength coefficient, | σf' | | 1100 MPa |
fatigue strength exponent, | b | | -0.1 MPa |
modulus of elasticity, | E | | 210,000 MPa |
fatigue ductility coefficient, | ef' | | 0.6 |
fatigue ductility exponent, | c | | -0.5 |
If the component were to be cycled under a fully reversed constant strain amplitude of 0.004, would you expect shot peening to influence observed fatigue life?
The first step is to calculate the transition life from:
The next step is to calculate the total strain amplitude at the transition life. This can be done by calculating either the elastic or plastic strain components at the transition life:
and so
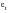
is given by
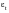
= 2 x 0.0016 =
0.0032The working strain amplitude of 0.004, is significantly larger than the strain amplitude at the transition and so the loading can be considered to fall within the low cycle regime. Under these circumstances shot peening should not be considered and is not providing any real benefit.
The Effect of Mean Stress
As mentioned above, most basic fatigue data are collected in the laboratory by means of testing procedures which employ fully-reversed loading (i.e., R = –1). However, most realistic service situations involve nonzero mean stresses. It is, therefore, very important to know the influence that mean stress has on the fatigue process so that the fully-reversed laboratory data can be usefully employed in the assessment of real situations.
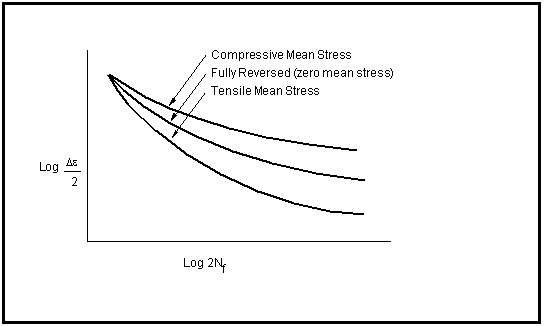
Figure 15‑39 Effect of Mean Stress on the Strain-Life Curve
Figure 15‑39 illustrates schematically the effect mean stress has on the strain-life curve. Typically, the effects are concentrated at the long life end of the diagram, with compressive means extending life and tensile means reducing it. At high strain amplitudes, mean stress relaxation occurs and any mean stress present tends towards zero. This effect is similar to the “washing out” of surface compressive stresses in the low-cycle regime.
The Morrow Mean Stress Correction
Morrow was the first to propose a modification to the baseline strain-life curve which can account for the effect of mean stress. He suggested that mean stress could be taken into account by modifying the elastic part of the strain-life curve by the mean stress,
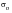
.
(15‑80)
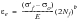
the entire strain life curve becoming:
(15‑81)
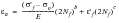
The Morrow equation is consistent with observation that mean stress effects are significant at low values of plastic strain and of little effect at high plastic strains.
The Smith-Watson-Topper Mean Stress Correction
Smith, Watson, and Topper have proposed a slightly different approach to account for mean stress through a consideration of the maximum stress present in any given cycle. In this case, the damage parameter is taken to be the product of the maximum stress,
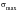
, and the strain amplitude,
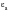
of a cycle.
For fully reversed loading, the maximum stress is give by
(15‑82)
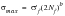
and by multiplying the strain-life equation by this term
(15‑83)
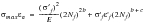
The Smith-Watson-Topper equation predicts that no fatigue damage can accrue when the maximum stress becomes zero or negative, which is not strictly true.
Morrow vs. Smith-Watson-Topper
It is difficult to categorically select one procedure in preference to the other. However, for loading sequences which are predominantly tensile in nature, the Smith-Topper-Watson approach is more conservative and is, therefore, recommended. In the case where the loading is predominantly compressive, particularly for wholly compressive cycles, the Morrow correction can be used to provide more realistic life estimates.
Factors Influencing Fatigue Life
A standardized, fully reversed, strain controlled, fatigue test is used to determine the baseline strain-life relationship for a polished specimen of approximately, 6mm diameter. If the fatigue or endurance limit measured by these means be denoted by
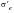
then the actual limit for a real component,
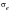
, must reflect all the modifications that come about in moving from a laboratory specimen to a component. For steels in particular, several empirical relationships have been developed which can account for the variation in
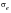
as a result of the following:
• Component size
• The type of loading
• The effect of surface finish
• The effect of surface treatment
The usual way to account for these effects is through the calculation and application of specific modifying factors so that
(15‑84)
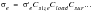
where reciprocal of the product, Csize Cload Csur, is collectively known as the fatigue strength reduction factor Kf, i.e.,
(15‑85)
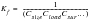
The approach tends to be conservative and the corrections are usually only applied at the endurance limit, the modifications required for the rest of the elastic portion of the strain-life curve are ill-defined. Typically, the procedure is to pivot the elastic strain (Basquin) curve about the 1000 cycles point.
The magnitude of the modification factors required to account for the various effects can be taken to be the same as that required to modify the basic nominal stress-life S-N curve. The manner in which the modifications are implemented is the same as that required for the nominal stress approach.
Application in MSC.Fatigue
The basic premise of the crack initiation or local stress-strain approach to fatigue life estimation is that the local fatigue response of a material at a critical location, for example the site of crack initiation at the root of a notch, is similar to that of a smooth specimen subjected to the same cyclic strains, see
Figure 15‑40.
Figure 15‑40 The Principle of Similitude
The Measured Strain Environment
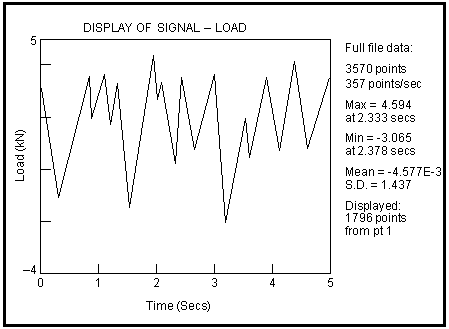
MSC.Fatigue requires representations of the load time histories in order to define the loading environment to which a component or structure is subject.
Figure 15‑41 A Load Time Series
It is very important to ensure that these measured load histories are indeed representative of the service environment experienced by the component in terms of both amplitudes and sequence. If, for example, the main source of fatigue damage is due to occasional “overloads”, such as the bump of a wheel on a pothole, or the “cold-hot-cold” (startup-run-shutdown) cycle of a large engine, as opposed to the cyclic loads associated with the continuous smooth operation, then large errors and misinterpretations can arise due to a misrepresentation of the important fatigue cycles.
Important: | In practice, in the ground vehicle industry in particular, experience has shown that 90 percent of fatigue damage accumulates from only 5 percent of induced fatigue cycles. |
Component Geometry and Stress Concentration
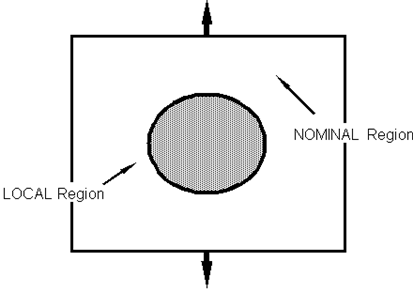
Up until now, the values of stress and strain discussed have been local to the area where fatigue damage accumulates. The finite element analysis translates a load (or set of loads) on a structure to a stress distribution across the component. Consequently, the FEA provides the local stress information at all locations but especially the points of stress concentration where fatigue problems are likely to occur during the life of the structure.
Figure 15‑42 Nominal and Local Critical Regions
In the diagram above, the critical location is at the edge of the hole, where the stress concentration will be a maximum. If conditions at both the nominal and local positions remain purely elastic, then the theoretical elastic stress concentration factor, Kt is equal to both the local stress concentration factor, K
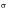
,
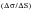
and the local strain concentration factor,
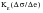
, so that:
(15‑86)
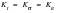
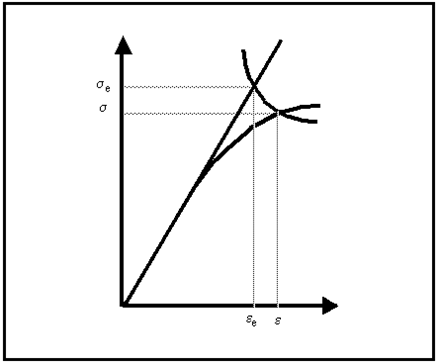
Under these conditions, NO damage can accumulate since fatigue only occurs as a result of reversed plastic flow. The basic rule for the crack initiation model is that fatigue damage, can only accumulate if at least some localized plasticity is present. In order to translate from the local elastic strains to the local elastic-plastic strains, MSC.Fatigue uses Neuber’s Rule.
Neuber’s rule asserts that the theoretical elastic stress concentration factor, Kt, is equal to the geometric mean of the local stress concentration factor,
and the local strain concentration factor,
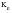
.
This relationship can be described as follows:
(15‑87)
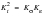
which may be rewritten as:
(15‑88)
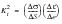
and finally:
(15‑89)
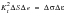
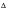 e | | The nominal strain range |
| | The local strain range |
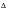 S | | The nominal stress range |
| | The local stress range |
On its own, Kt, can only account for the effect of geometry on the stresses and strains visible at a given location. Kt is not required in MSC.Fatigue since the linear static FEA has already calculated local elastic strains. However, in MSC.Fatigue, an additional Kt, is used which allows you to include the effect of manufacturing and environmental factors such as casting, fretting, corrosion, etc., if they are present.
The surface finish and treatment of a component can also change the local stress concentration and hence affect the fatigue life. However, MSC.Fatigue does not model this using a stress concentration factor since the effect is not equally important at all stress or strain levels. Instead, the high-cycle end of the life curve is modified to reflect a lowering of the endurance limit as reported by Lipson and Juvinall (Ref. 9). This is implemented by adjusting the slope of the elastic strain-life curve. See
Factors Influencing Fatigue Life, 1331.
Elastic-Plastic Corrections
The Neuber method is commonly used to estimate elastic-plastic stresses and strains at the roots of notches on the basis of elastic stress analysis. It applies where the yielding is limited in extent; under these circumstances it provides a reasonable approximation for the redistribution of stress and strain. When yielding is more widespread, for instance when loads are very high, or notches very shallow (or absent) it may give non-conservative predictions. The following methods address this problem through a consideration of behavior in the limit as the component becomes fully plastic.
Mertens-Dittmann method - Neuber’s rule is usually used to calculate elastic-plastic stress and strain from their wholly elastic theoretical equivalents such as might be estimated by an elastic finite element analysis.
So that with Kt taken as unity, i.e. using local elastic finite element stresses and strains:
(15‑90)
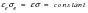
Both
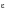
and
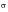
can be calculated from the above equation together with the equations for the cyclic stress-strain curve and twice the cyclic-stress strain curve.
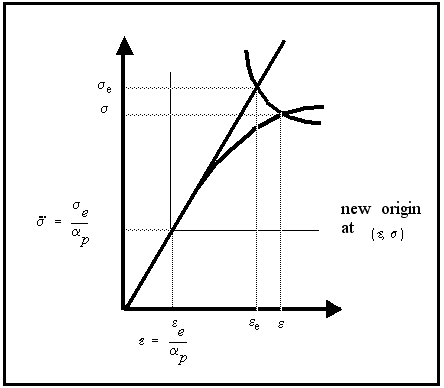
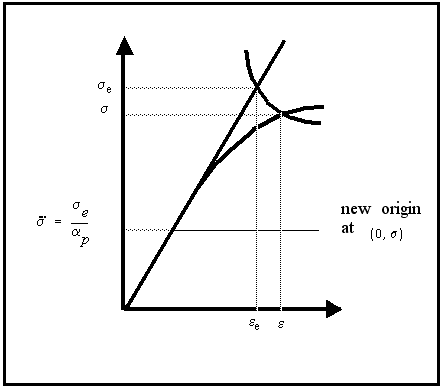
Dittmann (5) describes a modification to the conventional Neuber approach proposed by Mertens. He suggested that a better estimate of the local notch stress and strain can be obtained through a consideration of the minimum theoretical stress and strain which must exist, due to the applied load, in the absence of the notch. This approach requires that a new origin, at these minimum values, be used in the Neuber equation.
The modified form of the Neuber equation is then
(15‑91)
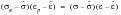
The plastic concentration or shape factor is defined by:
(15‑92)
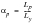
where Ly is the load that gives rise to first yielding and Lp the load required to cause plastic collapse. What this means in terms of the Neuber correction can best be understood by means of a example; consider a simple beam in bending. The bending moment required to produce yielding at the surface of a beam is given by:
(15‑93)
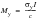
where I is the second moment of area of the beam and c is the distance of the extreme fibre from the neutral axis. As the moment increases the plastic layer will increase and the size of the elastic core will decrease. If the material is considered to be elastic-perfectly plastic, then the stress will not increase but stay fixed at the yield value. Eventually the plastic layer will penetrate right to the centre. The moment corresponding to this load is called the plastic moment and is given by:
(15‑94)
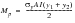
where y1 and y2 are the distances from the neutral axis to the centroids of the two yielded areas and A is the cross sectional area. For beams in bending then:
(15‑95)
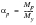
The value of the plastic strain concentration or shape factor
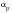
is a function of the shape of the beam. Some typical values for beams in bending are given below:
The normal Neuber correction will tend to underestimate the stress and strain at the surface of a beam in bending when there is more than a small degree of plasticity. When the origin used in the Neuber correction is shifted using the Mertens-Dittmann method, as the beam goes fully plastic, the Neuber hyperbola will be asymptotic to the plastic limit stress. The result is a more conservative prediction of stress and strain as plasticity spreads. Note the following points:
• The value of
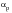
is a function of the loading type.
• When dealing with a notched component,
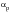
can be estimated from the product of
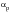
for the unnotched component and a Κ
t value for the notch.
• As
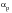
approaches infinity, the Mertens-Dittmann method reduces to the standard Neuber method.
Seeger-Beste method - The Seeger-Beste (6) method is very similar to the Mertens‑Dittmann method except that the origin is shifted only in the stress direction. This is best illustrated graphically:
Linear Damage Summation
A strain-based, constant amplitude, fatigue damage curve represents a set of tests at constant strain amplitude
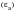
or STW parameter
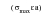
together with associated lives, see
Material Management (Ch. 3), for more details.
Operation at a strain amplitude
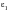
will result in failure in say N1 cycles. Operation at the same strain amplitude for a number of cycles less than N1, Nj say, will result in a smaller fraction of damage, Dj, which is often referred to as a partial damage. Operation over a spectrum of different strain levels, results in a partial damage contribution Di from each strain cycle,
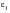
. Failure is then predicted when the sum of these partial damage fractions reaches unity so that:
(15‑96)
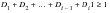
The Palmgren-Miner rule asserts that the partial damage at any strain amplitude
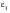
or STW value, is linearly proportional to the ratio of number of cycles of operation, ni, to the total number of cycles that would produce failure at that strain level, Ni, i.e.,
(15‑97)
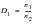
Failure is predicted then if:
(15‑98)
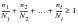
or
(15‑99)
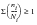
The above equations represent a statement of the linear damage rules used by both the stress-life and local strain fatigue life processors in MSC.Fatigue. Experience shows that linear damage summation is an over simplification of reality. The most important shortcoming is that no account is made of the sequence in which strain levels are experienced, and damage is assumed to accumulate at the same rate for a given strain level regardless of prehistory. In particular, it appears that large strain amplitudes which precede smaller ones, cause the smaller cycles to become more damaging than expected and vice versa. The net result is that in the first instance, the Miner sum
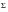
(F(n,Ν)) is measured to be less than 1. Since most service environments involve quasi-random loading sequences, the use of the Palmgren‑Miner linear damage rule summing to a constant of 1 is mostly satisfactory.
Important: | The Design Optimizer (DESOPT) does allow you to change the miner sum from the default value of 1.0 to any value between 0.01 and 2.0. |
Analytical Procedure
The strain-life method in MSC.Fatigue may be summarized as follows:
1. By means of linear static FEA, derive the local stress-strain time history from the load time histories. This includes superpositioning of multiple FEA/load time history load cases (or use stress-strain time history directly from linear transient or forced vibration FE analysis).
2. Extract the fatigue cycles in the local stress time history by means of the rainflow algorithm.
3. Make the elastic-plastic correction using Neuber’s rule.
4. Model the fatigue crack initiation process using hysteresis loop simulation based on the cyclic stress-strain curve.
5. Assess the damage contribution of each closed hysteresis loop by referring to the selected damage curve (strain-life, Morrow, STW curves).
6. Linearly sum the damage associated with each cycle by using Miner’s rule.
The Statistical Nature of Fatigue
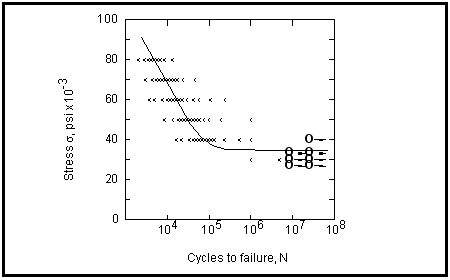
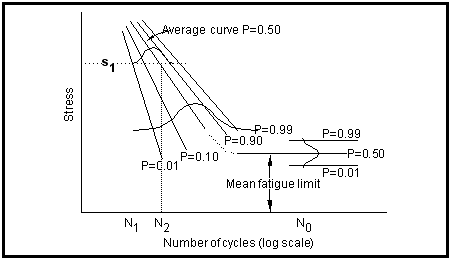
A considerable amount of time and effort has been expended in the statistical analysis of fatigue data and in exploring the reasons for variability in fatigue test results. Since both the fatigue life and fatigue limit are statistical quantities, as are most other measured parameters, it must be realized that considerable deviation from the average curve determined by only a few specimens is to be expected (see
Figure 15‑43). It is necessary to think in terms of the probability of a specimen attaining a certain life at a given stress or strain level or the probability of failure at a given level near the fatigue limit. To do this requires the testing of considerably more specimens than might be expected so that the statistical parameters for estimating these probabilities can be determined.
Figure 15‑43 Plot of Stress-Cycle (S-N) Data
Collected by Laboratory Testing
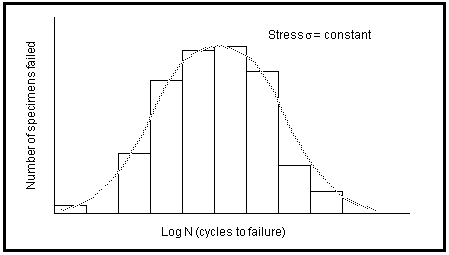
Figure 15‑44 Distribution of Fatigue Specimens Failed at Constant Stress Level
Representation of Fatigue Data on a Statistical Basis
Therefore, the basic method for expressing fatigue data should be a Wöhler line which has been expanded to form a surface representing the relationship between stress (or strain), number of cycles to failure and probability of failure. A distribution of fatigue life at constant stress is illustrated schematically in
Figure 15‑45 and based on this, curves of constant probability drawn. Thus, at standard deviation from mean,
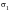
, 1 percent of samples would be expected to fail after N1 cycles, 50 percent after N2 cycles, etc. The figure also indicates a decreasing scatter in fatigue life with increase in stress, which is usually found to be the case.
Figure 15‑45 Representation of Fatigue Data on a Probability Basis
The Statistical Distribution Function
The statistical distribution function which describes the distribution of fatigue lives at a constant stress or strain level is not accurately known, since this would require the testing of over 1000 identical specimens under identical conditions at a constant stress. Researchers have tested up to 200 steel specimens at a single stress amplitude and have found that the frequency distribution of cycles to failure, Nf, followed the Gaussian, or normal, distribution if the fatigue life was expressed as log(Nf). For most engineering purposes, it is sufficiently accurate to assume a logarithmic normal distribution of fatigue life at constant stress in the region of the probability of failure of P = 0.10 to P = 0.90. However, it is frequently important to be able to predict fatigue life corresponding to a probability of failure of 1 percent or less. At this extreme limit of the distribution, the assumption of log-normal distribution of life is no longer justified, although it is frequently used. Alternative approaches have been proposed with the most commonly used one being the Weibull distribution.
Probability of Failure at a Finite Life
For a given stress or strain level, fatigue lives from a series of tests may be plotted on probability paper in order to estimate probability of failure. It is usual to use either log-normal or Weibull probability paper. To plot sample data in a meaningful way, the following procedure may be used:
• Order the array of data with the smallest value of life listed first.
• Assign a rank, r, to each data value (i.e., 1 to the first, 2 to the second, and n to the last — the longest life).
• Determine the plotting position for each data point by dividing its rank, r, by n+1, where n is the total number of measured lives.
• Plot the magnitude of the life at its corresponding plotting position on the chosen probability paper, either log-normal or Weibull.
Having plotted the data, the probability plot is examined for linearity. If the lives fall on a straight line, it may be concluded that the chosen distribution is appropriate.
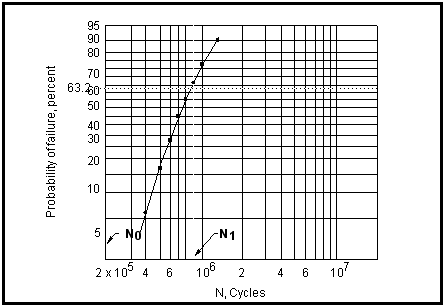
As an example of the procedure, consider the following table of lives for constant amplitude fatigue tests at 345 MPa.
Rank (r) | Cycles to Failure (x10-5) | Plotting Position
100r/(n+1) |
1 2 3 4 5 6 7 8 | 4.0 5.0 6.0 7.3 8.0 9.0 10.6 13.0 | 11.1 22.2 33.3 44.4 55.6 66.7 77.8 88.9 |
|
|
|
|
|
|
|
|
These data have been plotted in
Figure 15‑46, from which the mean, 50%, or characteristic, 63.2% lives can be read off directly. Extrapolation of the line to lower probabilities of failure are also possible.
Figure 15‑46 Weibull Plot for Fatigue Data
Probability of Failure for Infinite Life
Design for infinite life requires operating stresses which are all smaller than the fatigue limit. As with the main part of the Wöhler line, the fatigue limit itself can be treated as a statistical quantity. For a statistical interpretation of the fatigue limit, we are concerned with the distribution of stress at a constant fatigue life. The fatigue limit of steel was once considered to be a sharp threshold value, below which infinite life would prevail. However, it is now recognized that the fatigue limit is really a statistical quantity which requires special techniques for an accurate determination. For example, in a heat- treated alloy steel the stress range which would include the fatigue limits of 95% of all specimens tested could easily range from 280 - 360 MPa.
The statistical problem of accurately measuring fatigue limit is complicated by the fact that we cannot measure the individual value of fatigue limit for any given specimen. We can only test a specimen at a particular stress, and if it fails, then the stress was somewhere above the fatigue limit of the specimen. Since the specimen cannot be retested, even if it did not fail at the test stress, we have to estimate the statistics of the fatigue limit by testing groups of specimens at several stresses to see how many fail at each stress.
Several testing procedures have been evolved for making statistical estimates. Two of the most commonly used procedures are known as Probit analysis and the staircase method. It is beyond the scope of this course to detail these procedures, however, if the reader is interested a good account may be found in “Guide for Fatigue Testing and the Statistical Analysis of Fatigue Data” ASTM STP 91-A, 2 edition, 1963.
Handling Statistics Under Random Loading Conditions
The statistical concepts outlined above have been and remain mainly applicable to fluctuating stresses which have a constant amplitude, rather like the rotation of Wöhler's railway axles. However, the nature of the fatigue problems being addressed today requires the treatment and handling of random loading situations. Clearly, the log-normal or Weibull probability approaches involving probability paper would be totally inappropriate for use in fatigue life estimation of real field data consisting of several thousand, if not millions, of data values. Several factors have come together to meet this challenge of providing statistical information during the process of fatigue life estimation.
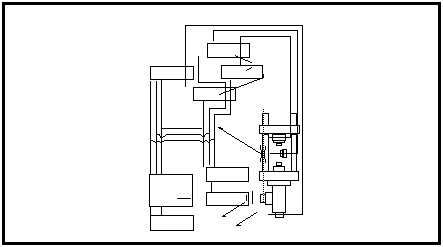
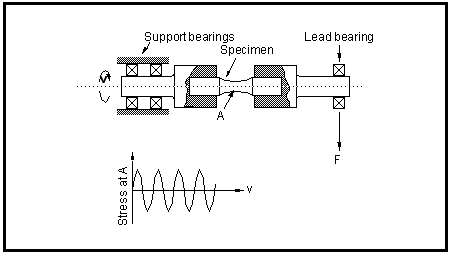
In the late 1960s, the switch away from the so-called nominal stress, S-N, based fatigue approach to the local stress-strain approach led workers to design fatigue testing procedures which are inherently much more precise. It became necessary to control and measure local stresses and strains during the fatigue test and so the “bubble of uncertainty” associated with these parameters in a nominal S-N test was dramatically reduced. Great improvements in laboratory testing procedures, compare
Figure 15‑47 and
Figure 15‑48, were required to achieve the necessary accuracy in the results, and this has gone a long way towards reducing the scatter in measured data and so mitigating the extent of the effect. That is not to say of course that such errors do not remain a problem, they are just less visible.
In addition to this, the need to process large amounts of data, together with the advent of low cost computing has meant that procedures have been developed for on-line statistical analyses, which whilst being firmly based on the principles outlined above, differ in their execution.
Figure 15‑49 illustrates the difference in approach.
Instead of considering the life at a particular stress or strain level to be distributed according to some chosen distribution, such as log-normal or Weibull, it is convenient to think of the stress or strain being distributed, at any life, according to the same distributions. In
Figure 15‑49 for example, the strain-life curve is made up of two components; the plastic strain
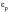
, and the elastic strain,
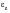
.
Figure 15‑47 Schematic Diagram of a Computer-Controlled
Closed-Loop Fatigue Testing Machine
Figure 15‑48 Rotating-Bending Fatigue Testing Machine of the Cantilever Bending Type
The equation of the strain-life curve may then be written as:
(15‑100)
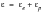
otherwise
(15‑101)
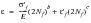
Where 2Nf represents the number of reversals, half cycles to failure, and the other parameters are material constants. This equation can now be expressed statistically in terms of probability of survival:
(15‑102)
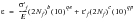
q | | the number of standard errors from the mean life |
e | | the standard error of 2Nf for the elastic life line |
p | | the standard error of 2Nf for the plastic life line |
Typically, the elastic and plastic component standard errors can be calculated directly from the results of the log elastic and log plastic vs. log reversals regression analyses, generally:
(15‑103)Std. Error =
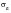
(1 - r
2)
0.5
| | the standard deviation of log(ε) either elastic or plastic |
r | | the regression correlation coefficient. |
For a normal distribution, the following values of 'q' can be assumed:
No. of Standard Errors from Mean, q | Probability of
Survival (% |
-3 -2.33 2 -1.28 -1 0 1 1.28 2 2.33 3 | 99.87 99 97.7 90 84 50 16 10 2.3 1 0.13 |
|
|
|
|
|
|
|
|
|
|
For example, if the following material parameters are assumed:
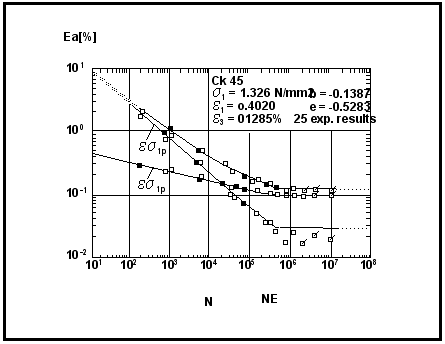
=εf' | =- | =0.4 |
=σf' | =- | =1326 MPa |
=c | =- | =-0.528 |
=b | =- | =-0.139 |
=E | =- | =205000 MPa |
=se | =- | =0.023 |
=sp | =- | =0.067 |
Then the following values of reversals to failure, 2Nf, can be calculated for a 10% and 90% probability of survival.
Specimen | Probability of
Survival (%) |
Plastic, 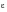 ’ fElastic, 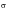 ’ f(MPa) Reversals 2Nf | 50 0.400 1326 1769 | 10 0.456 1417 2307 | 90 0.350 1240 1355 |
|
|
|
which means that there is a 90% chance that the specimen will survive 1355 reversals and only a 10% chance it will survive 2307 reversals.
In the above examples, we have assumed values of q, the number of standard deviations from the mean, for a log-normal distribution. It would be equally valid to use values which represent the Weibull distribution. Indeed, for confidence levels greater than 90% it is recommended to use Weibull.
This approach is by no means confined to a treatment of strain-life curves, S-N curves can also be considered by these means. See, for example,
Figure 15‑50.
Figure 15‑49 Strain-Life Curve Made Up of Elastic and Plastic Components
Figure 15‑50 Weibull Approach With S-N Curves
The Absolute Accuracy of Fatigue Life Estimation
From the above discussion, it has been indicated that fatigue life is a rather statistical quantity to which it is very difficult, if not impossible to ascribe a unique value. It has been shown that the material law used to describe the fatigue response of a material, the Wöhler line (stress or strain), is itself not unique and must be treated as a statistical quantity. However, Wöhler lines are amenable to statistical treatment and so a measure of the variability resulting from the determination of material properties can be defined. In addition to this variability, other sources of error can and most often do arise.
Errors in the measured loading environment can also lead to errors in calculated life. As a rule of thumb, a 10% error in strain or stress measurement can either halve or double life, all else being equal. Similarly, errors in the description of component geometry can lead to significant variations. For this reason, and for complicated geometries in particular, finite element analysis may be used to describe the state of stress at any point within a structure with greater accuracy.
Taking all these factors into account, today the state of the predictive art with respect to fatigue life is to within between a factor of two or three of the actual, which itself is not a unique number. Expressing this mathematically it is possible to say, for any given calculated life, Lc, the largest scatter band we should expect is given by the expression:
(15‑104)
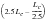
If our life estimates are significantly more widely scattered than this, then a major error in one or more of the inputs to the analysis has been made and must be sought out if the predictive process is to continue.