XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> 1.5 Thermal Analysis
Thermal problems can be categorized as steady-state or transient, linear or nonlinear. Transient analyses are characterized by solution evolution over time, and in addition to energy exchange with the environment, involves thermal energy storage. Steady-state analyses are concerned with state point solutions to fixed boundary condition problems.
Nonlinearities enter into both steady-state and transient solutions through several areas. The most common nonlinearity is associated with temperature dependent material properties, in particular thermal conductivity and specific heat. Other nonlinearities are introduced from application of boundary conditions principally convection and radiation. All nonlinear analyses necessarily involve solution iteration, error estimation, and some form of convergence criteria. MD Nastran attempts to do this as efficiently and trouble free as possible.
Steady-State Analysis
The most general form of the steady-state heat balance equation is as follows:
(1‑4)
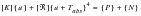
[K] | = | =the heat conduction matrix |
| = | =the radiation exchange matrix |
{u} | = | =the vector of unknown temperatures |
Tabs | = | =the temperature offset from absolute required for radiation
calculations (absolute temperature) |
{P} | = | =the vector of constant applied heat flows |
{N} | = | =the vector of temperature dependent heat flows |
This equation is inherently nonlinear due to the presence of the fourth power law radiation term. In addition to the radiation term, many other nonlinearities may be introduced into this equation through the coefficient matrices and boundary condition terms. Specifically, nonlinearities are introduced by specifying the material properties and boundary conditions as temperature dependent as discussed in the
Thermal Material Properties, 5 and
Thermal Loads and Boundary Conditions, 7.
MD Nastran applies a Newton-Raphson iteration scheme for the solution of these nonlinear equations. This process leads to the following form of the heat balance equation:
(1‑5)
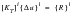
| = | =the tangential conductance matrix |
= 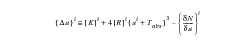 |
| = | =the residual vector {P}i + {N}i - [K]i {u}i - [R]i {ui + Tabs}4 |
At each iteration, the left-hand side matrix and the right-hand side vector are computed based on the temperature from the previous iteration

. By solving for the unknown vector
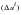
, the new temperatures
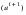
can be determined:
(1‑6)
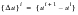
or
(1‑7)
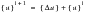
Because of the expense of performing matrix decompositions, MD Nastran recalculates the residual vector at each iteration, but only recalculates the tangent matrix when convergence is illusive or if it will lead to improvement in the iteration efficiency. MD Nastran will attempt to achieve an optimum converged solution by balancing various solution aspects such as: load bisection, residual updates, tangent matrix updates, line searches, and BFGS updates. Further description of the methods employed can be found in Reference 2. (p. 14).
For steady-state analysis, the defaults for controlling the nonlinear solution should be sufficient for most problems. For those problems where additional control is required, the convergence tolerances for Temperature, Load, and Work can be overridden. See
Steady-State and Transient Convergence Criteria, 14 for more information.
Initial Conditions in Steady-State Analysis
Since the nonlinear equations are solved by an iterative scheme, careful consideration of the initial conditions can have a significant effect on how quickly a problem will converge, or if it will converge at all. The initial conditions provide the starting point temperatures for the iterative solution method. Clearly, if we were able to exactly guess the solution to our problem, the process would converge on the first iteration, as it must for linear analysis. Although this is highly unlikely, a good initial guess can speed up the convergence process significantly. For highly nonlinear problems, good initial temperature estimates may be required in order to achieve convergence. See
Initial Conditions in Transient Analysis, 14 for more information.
Transient Analysis
The most general form of the transient heat balance equation is:
(1‑8)
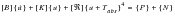
where, in addition to the terms already defined in the steady-state equation, we have:
(1‑9)[B] = the heat capacity matrix.
(1‑10)
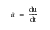
Because of its transient behavior, this equation must be integrated over time. The numerical method implemented for performing the time integration is Newmark’s method. As in the steady-state case, this equation also can be extensively nonlinear due to radiation and temperature-dependent material properties and boundary conditions. As a result, nonlinear iterations are also required for the solution of this equation. The iteration is performed within each time step until a converged solution for that time step is achieved (see Reference 2. (p. 14) for more details).
Transient analysis requires specifying the total solution time. Solution time is defined by the initial time step size and total number of time steps requested. The total solution time is determined from their product. Because MD Nastran employs an automatic time stepping scheme (i.e., the time step is varied by the solver as the solution progresses), the actual number of time steps used may ultimately be quite different from the input request. In any event, the total amount of solution time will be approximately equal to the initially calculated product within some small tolerance of the last time step size. The advantage of using the adaptive time step algorithm is the potential for significantly reduced run times.
To avoid inaccurate results or unstable solutions, the proper choice of the initial time step is required. A responsible initial time step is dependent on a number of factors, including the spatial size of the element mesh and the thermal diffusivity of the material. The selection criteria is:
(1‑11)
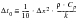
| = | =the initial time step |
| = | =the mesh size |
ρ | = | =the density |
Cp | = | =the specific heat |
k | = | =the conductivity |
Initial Conditions in Transient Analysis
Initial conditions define the temperature starting point for a transient analysis. Every node in the problem must have an initial temperature explicitly defined. Any node that does not have an initial temperature defined will automatically have a temperature of 0.0 assigned to it. This default temperature can be changed in the Solution Parameters form for the given application, either steady-state or transient analysis.
Caution must be exercised when specifying initial conditions relative to any specified temperatures defined via a boundary condition. The initial condition temperature for these nodal points must match the (Implicit and Explicit) boundary condition temperature at time equal to zero. Failure to match these temperatures will cause an initial jump in the solution that can make convergence difficult to achieve. Fortunately, the default analysis setup will automatically enforce these temperatures to be equal at the start of the problem.
Steady-State and Transient Convergence Criteria
As discussed previously, the solution of the nonlinear equations requires an iteration scheme. Efficient iteration schemes are highly dependent on convergence criteria and error estimation. Convergence criteria provide a means of measuring solution error relative to some predetermined acceptable level. For each iteration performed during the solution process, error levels are calculated and compared with preset tolerances. Three convergence criteria are available within MD Nastran that measure error based on temperature, load, and work. These criteria apply to steady-state and transient solutions alike.
Four recommendations regarding nonlinear convergence can be made:
1. For most problems, use the default criteria selection with their default tolerance values.
1. If the analysis is transient and involves any time-varying temperature boundary conditions, you must use the temperature convergence criteria.
1. Convergence may be enhanced by increasing the numerical tolerance levels from their default values.
1. For highly nonlinear transient problems, the maximum number of iterations per time step may be increased.
The defaults for controlling the nonlinear solution should be sufficient for most problems. However, for those problems requiring additional control, the convergence tolerances for Temperature, Load, and Work can be overridden. (In the solution of heat transfer problems, a convergence criteria based on WORK is realistically just a mathematical construct representing an extension of the equations used in the comparable structural solver.)