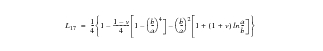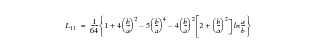XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> 14.2 Validation Problems
Problem 1: Linear Statics, Rigid Frame Analysis
Solution/Element Type:
MSC Nastran, Solution 101, Linear Statics, CBAR Bar Elements with Standard Formulation
Reference:
Roark, R.J., and Young, W.C., Formulas For Stress and Strain, 5th ed., McGraw-Hill, Inc., 1975, pp. 122-126.
Problem Description:
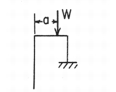
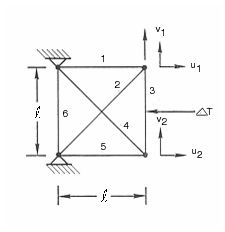
A rigid frame with uniform properties is subjected to a concentrated force midspan of the top horizontal member. One end of the frame is fixed while the other is free. Find the horizontal and vertical displacements as well as the rotation at the free end of the frame. 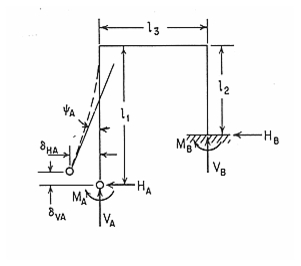
Engineering Data:
Theoretical Solution:
Upon substitution of the engineering data into the equations below, the following results are obtained:
MSC Nastran Results:
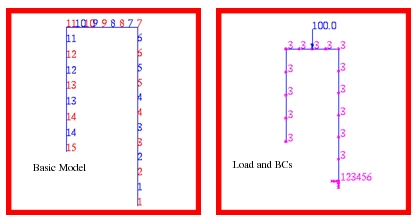
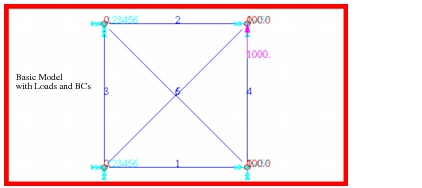
To determine the deflections at the free end of the frame, the model shown in Figure 14‑1 was created. This model consisted of 14 MSC Nastran
CBAR elements. Each bar was assumed to have a square cross-section of 0.5 x 0.5 inches. This gives a cross-sectional moment of inertia of 0.0052083 in4 that is identical to what was assumed in the preceding calculations. Using this model, the following results were obtained.
Table 14‑2 Source | | | |
MSC Nastran* | 0.10368 | -0.16706 | 0.042243 |
Theory | -0.10368 | -0.16664 | -0.042240 |
%, Difference | 0.0% | 0.252% | 0.007% |
*MSC Nastran results have opposite sign due to the reversal of the direction of x and z axes of the global coordinate frame relative to the theoretical results coordinates.
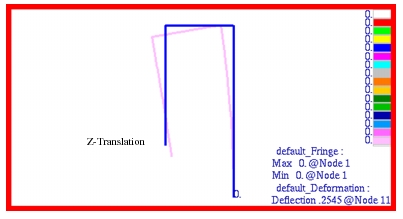
The corresponding deformed shape plot that was made for the rigid frame is shown in
Figure 14‑2 where the deformed shape has been superimposed upon the undeformed mesh. Fringe plots for the x, y, and z components of the translational displacements that were generated with Patran are shown in
Figure 14‑3,
Figure 14‑4 and
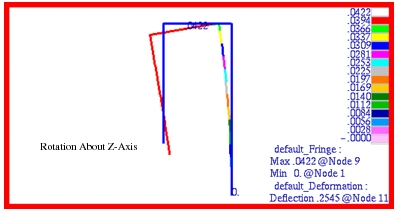
Figure 14‑5, respectively. The fringe plot for the rotation about the z axis is shown plotted in
Figure 14‑6. All fringe plots are displayed on the fully deformed structure. Examination of these fringe plots near the free end of the frame clearly shows that the Patran results are identical to the preceding MSC Nastran results.
File(s): <install_dir>/results_vv_files/prob001.bdf, prob001.op2
Figure 14‑1 Basic FE Model of Rigid Frame with Load and BCs.
Figure 14‑2 Deformed and Undeformed Shape of Rigid Frame.
Figure 14‑3 X-Translational Deformation of Rigid Frame.
Figure 14‑4 Y-Translational Deformation of Rigid Frame.
Figure 14‑5 Z-Translational Deformation of Rigid Frame.
Figure 14‑6 Rotational Displacement about Z-axis of Rigid Frame.
Problem 2: Linear Statics, Cross-Ply Composite Plate Analysis
Solution/Element Type:
MSC Nastran, Linear Statics, Solution 101, CQUAD4 Elements with Standard Formulation and Laminated Material Properties.
Reference:
Jones, R. M., Mechanics of Composite Materials, Hemisphere Pub. Corp., 1975, pp. 198-201.
Problem Description:
A flat rectangular plate is made from a cross-ply 0/90/0 degree ply stacking. Assuming that the plate is cured at 270o F, find the stress in each of the plies once the plate is cooled down to 70o F.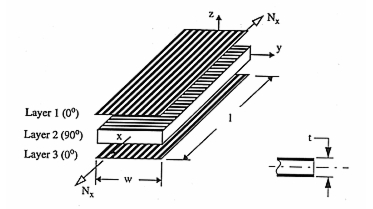
Engineering Data:
Theoretical Solution:
Only the stresses in plies 1 and 2 are shown since the laminate is symmetric about its midplane. Hence, ply 1 is identical to ply 3. In the expressions below, 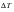 refers to the temperature difference between the curing temperature for the laminate and its final operational temperature. In this particular example,
refers to the temperature difference between the curing temperature for the laminate and its final operational temperature. In this particular example, 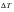 would equal -200o F. Because of the absence of any localized restraint to thermal shrinkage coupled with isotropic thermal expansions, the stresses in each ply are uniform. The predicted stresses are as follows for
would equal -200o F. Because of the absence of any localized restraint to thermal shrinkage coupled with isotropic thermal expansions, the stresses in each ply are uniform. The predicted stresses are as follows for 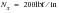 ,
, 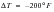 and
and 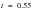 in:
in: MSC Nastran Results:
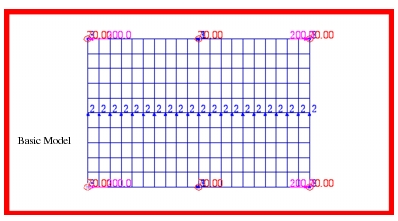
To predict the stresses in the cross-ply laminate for this problem, a model was created that consisted of CQUAD4 elements with laminate properties specified by a MSC Nastran
PCOMP data entry. This permitted stress recovery to be performed on a ply by ply basis. Due to symmetry, any motion along the vertical and horizontal planes of symmetry was restrained out. In addition, all out of plane deformations were restrained since a balanced cross-ply laminate should remain flat during cool down. Application of these boundary conditions avoided any potential problems with unrestrained rigid body motion. The applied loads and boundary conditions are also shown superimposed upon the finite element mesh in Figure 14‑7. Using this model, the following results were obtained with MSC Nastran.
Table 14‑3 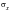
Source | | | |
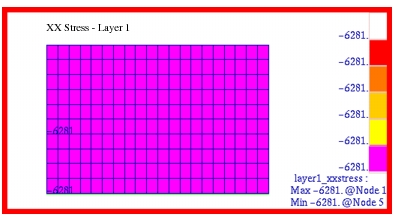
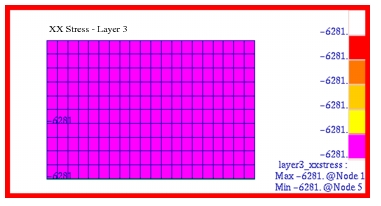
MSC Nastran | -6280.51 | 1691.68 | -6280.51 |
Theory | -6274.55 | 1692.73 | 6274.55 |
%, Difference | 0.095% | -0.062% | 0.095% |
Table 14‑4 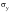
Source | | | |
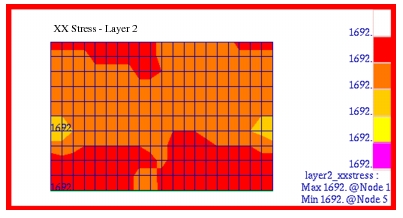
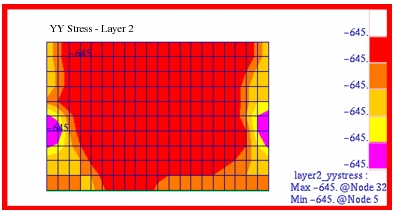
MSC Nastran | 3228.55 | -645.29 | 3228.55 |
Theory | 3243.64 | -648.73 | 3243.64 |
%, Difference | -0.465% | -0.530% | -0.465% |
Table 14‑5 
Source | | | |
MSC Nastran | -0.002043 | 0.000551 | -0.002043 |
Theory | 0.0 | 0.0 | 0.0 |
%, Difference | - | - | - |
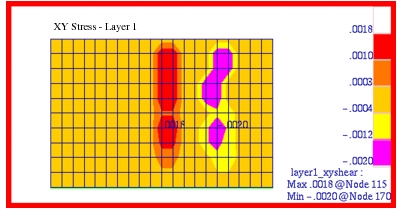
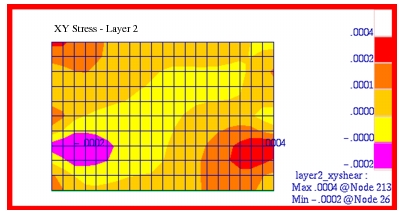
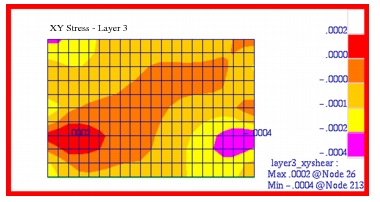
The corresponding fringe plots that were generated with Patran for the x-, y- and xy shear stress components in each of the plies are shown in
Figure 14‑8 through
Figure 14‑16. A comparison of these plots with the preceding MSC Nastran results clearly shows that the two are identical. Layer 1 and 3 were plotted in the element coordinate system; layer 2 was plotted in the Global coordinate system. You must read in the .bdf file below to be able to perform the correct coordinate transformation to reproduce the layer 2 plots.
Files: <install_dir>/results_vv_files/prob002.bdf, prob002.op2
Figure 14‑7 Basic Cross-Ply FE Composite Plate Model.
Problem 3: Linear Statics, Principal Stress and Stress Transformation
Solution/Element Type:
MSC Nastran, Solution 101, Linear Statics, CQUAD4 Elements with Standard Formulation.
Reference:
Popov, E.P., Introduction to Mechanics of Solids, Prentice-Hall, Inc., 1968, pp. 337-340.
Roark, R.J., and Young, W.C. , Formulas For Stress and Strain, 5th ed., McGraw-Hill, Inc., 1975, pp. 62, 93 - 96, 101.
Problem Description:
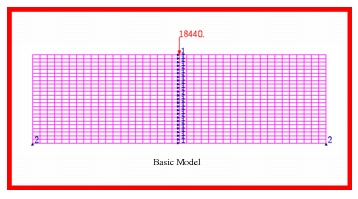
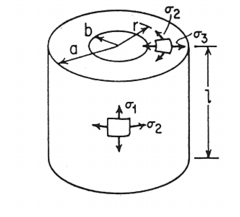
A weightless rectangular beam spans 40 inches and is loaded with a vertical downward force W = 18.44 kips at midspan. Find the principal stresses at points a, b, c, b’ and a’.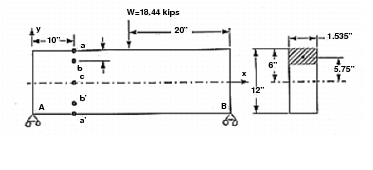
Engineering Data:
Theoretical Solution:
Reaction Loads:
Transverse Shear Force:
where
Moments:
Fiber and Shear Stresses:
Here A’ is the area of that part of the section above (or below if the point of interest is located below the beam’s neutral axis) the point of interest and y’ is the distance from the neutral axis to the centroid of A’ as shown below.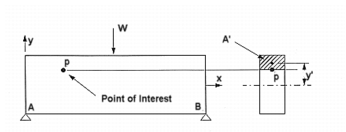
Stress at a:
Stress at b:
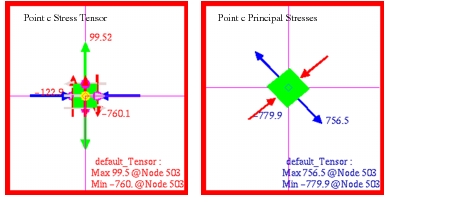
Stress at c:
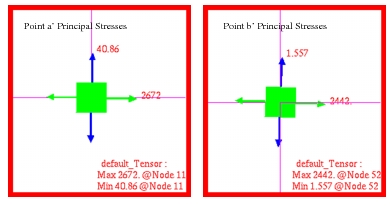
Stress at b’:
Stress at a’:
Based upon these fiber and shear stresses, the following principal stresses are calculated: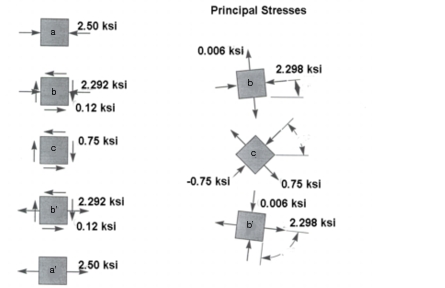
MSC Nastran Results:
To determine the stress state in the beam, a MSC Nastran
model was generated using Patran
. To maximize accuracy, a mesh density was chosen so that nodes would be precisely situated at every designated stress recovery point. In addition, to prevent any out of plane deformation, all displacements normal to the plane of the model were fully restrained, thereby imposing a plane strain condition. Furthermore, to prevent any longitudinal rigid body translation, a symmetry boundary condition was imposed at midspan the entire height of the beam. The imposed boundary conditions and applied loads are shown in Figure 14‑17 superimposed upon the mesh, which consisted solely of CQUAD4 elements using a standard formulation. Using this model, the following stresses were predicted at points a, b, c, b’ and a’. Table 14‑6 Source | | | Max Principal | Min Principal |
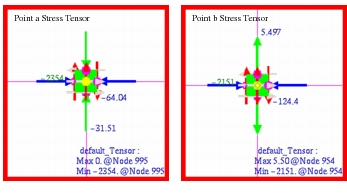
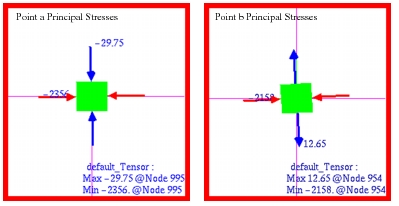
MSC Nastran | -2354. | -64.04 | -29. 75 | -2356. |
Theory | -2500. | 0.0 | 0.0 | -2500. |
%, Difference | -5.85% | - | - | -5.76% |
Table 14‑7 Source | | | Max Principal | Min Principal |
MSC Nastran | -2151. | -124.4 | 12.65 | -2158. |
Theory | -2290. | -120.0 | 6.00 | -2298. |
%, Difference | -6.07% | 3.67% | 110.8% | -6.09% |
Table 14‑8 Source | | | Max Principal | Min Principal |
MSC Nastran | -122.9 | -760.1 | 756.5 | -779.9 |
Theory | 0.0 | -750.0 | 750.0 | -750.0 |
%, Difference | - | 1.35% | 0.867% | 3.99% |
Table 14‑9 Source | | | Max Principal | Min Principal |
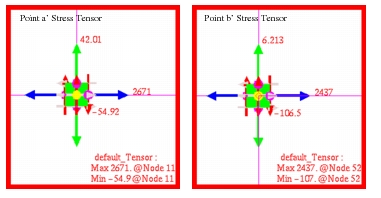
MSC Nastran | 2437. | -106.5 | 2442. | 1.557 |
Theory | 2290. | -120.0 | 2298. | 6.00 |
%, Difference | 6.42% | -11.3% | 6.27% | -74. 05% |
Table 14‑10 Source | | | Max Principal | Min Principal |
MSC Nastran | 2671. | -54.92 | 2672. | 40.86 |
Theory | 2500. | 0.0 | 2500. | 0.0 |
%, Difference | 6.64% | - | 6.88% | - |
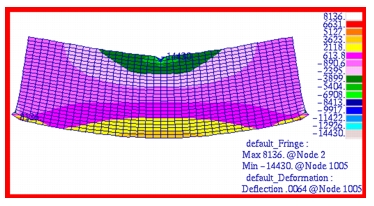
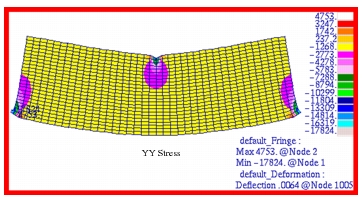
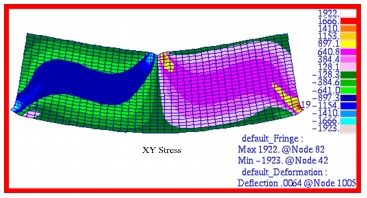
The Patran fringe plots that were made of the x-, y- and xy- stress components are shown in
Figure 14‑18,
Figure 14‑19, and
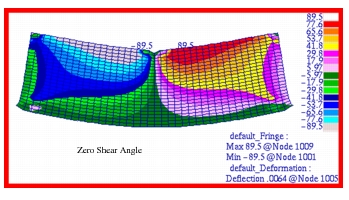
Figure 14‑20 respectively. In addition, the orientation angle for the max principal stress, or zero shear angle, has been plotted in
Figure 14‑21. To better show the stress state at each of the designated stress recovery points, tensor plots were made of the fiber stress as well as the principal stress at each position, starting with
a and proceeding onto
a’. These are shown in
Figure 14‑22 through
Figure 14‑26. Examination of the Patran tensor and fringe plots reveals that they are identical to the preceding MSC Nastran results.
File(s): <install_dir>/results_vv_files/prob003.bdf, prob003.op2
Figure 14‑17 Basic Beam Model with Loads and Boundary Conditions.
Figure 14‑21 Orientation Angle of Maximum Principal Stress.
Figure 14‑22 Stress Tensor at Points a and b.
Figure 14‑23 Principal Stresses at Points a and b.
Figure 14‑24 Stress Tensor at Points a’ and b’.
Figure 14‑25 Principal Stresses at Points a’ and b’.
Figure 14‑26 Stress Tensor and Principal Stresses at Point c.
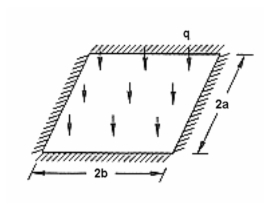
Problem 4: Linear Statics, Plane Strain with 2D Solids
Solution/Element Type:
MSC Nastran, Linear Statics, Solution 101, CQUAD4, CQUAD8, CTRIA3, CTRIA6, CQUADR and CTRIAR Elements with Standard and Revised Formulations
Reference:
Roark, R. J., and Young, W. C., Formulas For Stress and Strain, 5th ed., McGraw-Hill, Inc., 1975, p. 504.
Problem Description:
An infinitely long, thick walled, cylinder is subjected to a uniform internal pressure. Assuming near incompressible material behavior, find the radial displacement as well the radial and hoop stress at the inner diameter (ID) and outer diameter (OD) of the cylinder.
Engineering Data:
| |
E=1000. psi |
|
a = 9.0 inches |
b = 3.0 inches |
q = 100. psi |
Theoretical Solution:
For the case of an internally pressurized thick walled cylinder, the displacement and stresses at the inner and outer radius are given by the equations below. Upon substituting the assumed values for  , the following displacements and stresses are calculated:
, the following displacements and stresses are calculated: MSC Nastran Results:
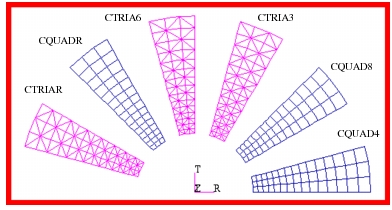
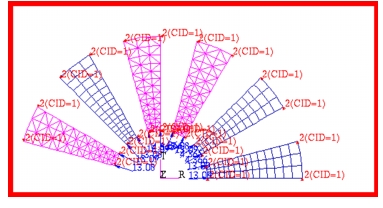
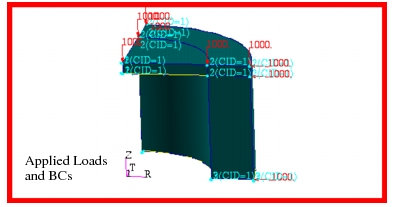
For the purposes of this problem, a 15 degree segment was modeled of the cross-section of the pipe with the appropriate axisymmetric boundary conditions being applied to the lateral edges of the model. In addition, five individual segments were modeled that were meshed with either CQUAD4, CQUAD8, CTRIA3 or CTRIA6 elements using a standard formulation or CQUADR and CTRIAR elements with a revised formulation. This was done to assess how variations in element topology and formulation affect overall accuracy of the results when performing a plane strain analysis with a high Poisson’s ratio. The actual model that was generated with Patran
is shown in Figure 14‑27 where the individual element types associated with each segment have been identified. The loading and boundary conditions that were applied to the model are shown in Figure 14‑28. Using the aforementioned model, the following results were obtained for each of the various element types.
Table 14‑11 
| CQUAD4 | CQUAD8 | CTRIA3 | CTRIA6 | CQUADR | CTRIAR |
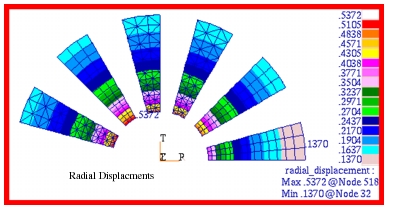
MSC Nastran* | .1370 | .1690 | .1680 | .1689 | .1755 | .1726 |
Theory | .2250 | .2250 | .2250 | .2250 | .2250 | .2250 |
%, Difference | -39.11% | -24.89% | -25.33% | -24.93% | -22.00% | -23.29% |
Table 14‑12 
| CQUAD4 | CQUAD8 | CTRIA3 | CTRIA6 | CQUADR | CTRIAR |
MSC Nastran* | .4102 | .5060 | .5031 | .5058 | .5357 | .5256 |
Theory | .5250 | .5250 | .5250 | .5250 | .5250 | .5250 |
%, Difference | -21.87% | -3.62% | -4.17% | -3.66% | 2.04% | 0.11% |
Table 14‑13 
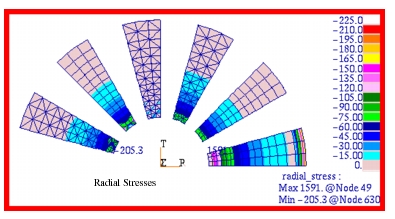
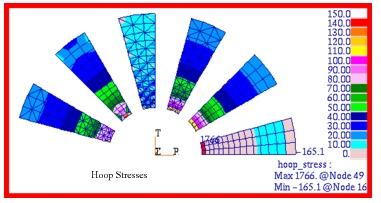
| CQUAD4 | CQUAD8 | CTRIA3 | CTRIA6 | CQUADR | CTRIAR |
MSC Nastran* | -165.1 | 25.32 | 25.00 | 25.01 | 25.30 | 26.44 |
Theory | 25.00 | 25.00 | 25.00 | 25.00 | 25.00 | 25.00 |
%, Difference | -760.40% | 1.28% | 0.0% | 0.04% | 1.20% | 5.76% |
Table 14‑14 
| CQUAD4 | CQUAD8 | CTRIA3 | CTRIA6 | CQUADR | CTRIAR |
MSC Nastran* | 1766. | 129.4 | 124.0 | 124.3 | 131.7 | 129.3 |
Theory | 125.00 | 125.00 | 125.00 | 125.00 | 125.00 | 125.00 |
%, Difference | 1312.8% | 3.52% | -0.80% | -0.56% | 5.36% | 3.44% |
Table 14‑15 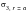
| CQUAD4 | CQUAD8 | CTRIA3 | CTRIA6 | CQUADR | CTRIAR |
MSC Nastran* | -186.0 | .3775 | .7289 | .0476 | 3.809 | -3.039 |
Theory | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
%, Difference | - | - | - | - | - | - |
Table 14‑16 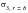
| CQUAD4 | CQUAD8 | CTRIA3 | CTRIA6 | CQUADR | CTRIAR |
MSC Nastran* | 1591.0 | -94.52 | -91.00 | -99.47 | -52.96 | -119.6 |
Theory | -100.0 | -100.0 | -100.0 | -100.0 | -100.0 | -100.0 |
%, Difference | 1691% | - 6.48% | -9.00% | -.53% | -47.04% | 19.60% |
* Represents average of all edge nodal values with nodal values averaged across adjacent elements.
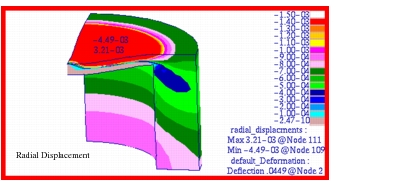
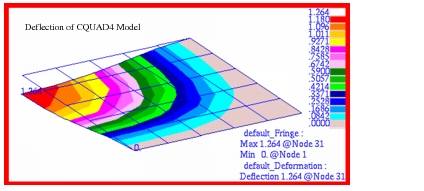
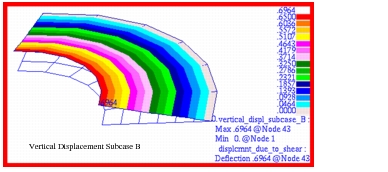
The fringe plot that was generated for the radial displacement is shown in
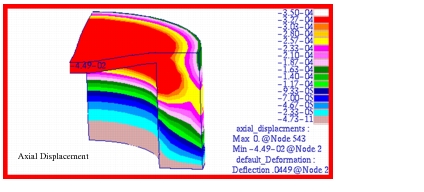
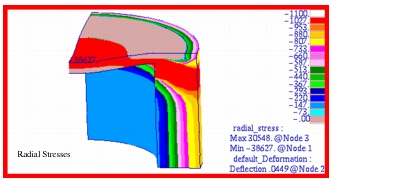
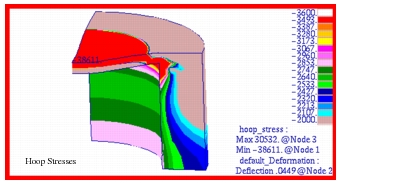
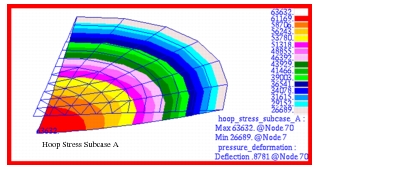
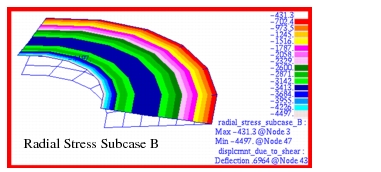
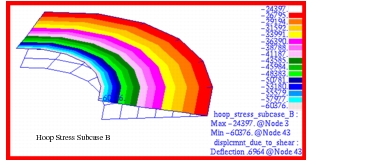
Figure 14‑29. Fringe plots for the radial and hoop stress are shown in
Figure 14‑30 and
Figure 14‑31. Here the stresses have been plotted with an adjusted scale that better shows the stress gradient present in each of the segments. All plots have been transformed into the cylindrical coordinate system defined in the problem. A comparison with the preceding tabular results clearly shows that Patran is accurately reproducing the MSC Nastran results.
The preceding results clearly demonstrate the wide degree of variability in the result attributable to element topology as well as formulation. Consistently, the higher order CQUAD8 and CTRIA6 elements gave superior performance compared to their linear counterparts. Similarly, in this application where cylindrical geometry was involved, a triangular element gave far more accurate results then compared to a quadrilateral element. Only by adopting the revised formulation of a CQUADR could acceptable results be obtained with a quadrilateral element. This would not be unexpected since the removal of any membrane-bending coupling produces far less sensitivity to extreme values in Poisson’s ratio as in this example.
File(s): <install_dir>/results_vv_files/prob004.bdf, prob004.op2
Figure 14‑27 Basic Models Using 2D Solid Elements.
Figure 14‑28 Loads and Boundary Conditions of 2D Solid Models.
Figure 14‑29 Fringe Plot of Radial Displacement on 2D Solids.
Problem 5: Linear Statics, 2D Shells in Spherical Coordinates
Solution/Element Type:
MSC Nastran, Linear Statics, Solution 101, CQUAD4 and CTRIA3 with Standard Formulation
Reference:
Roark, R. J., and Young, W.C., Formulas For Stress and Strain, 5th ed., McGraw-Hill, Inc., 1975, p. 451.
Problem Description:
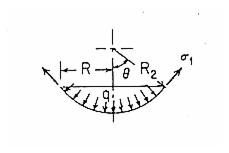
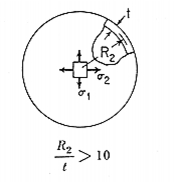
A section of a thin, spherical shell is internally pressurized. The free edge of the shell is restrained in the meridional direction. Find the stresses and displacements of the shell.
Engineering Data:
t = 0.05 in | |
R2 = 10.0 in |
q = 200.0 psi |
|
E = 1.0 x 107 psi |
|
Theoretical Solution:
For the case of an internally pressurized spherical shell tangentially supported, the predicted stresses and displacements are, after substituting the assumed values for
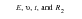 :
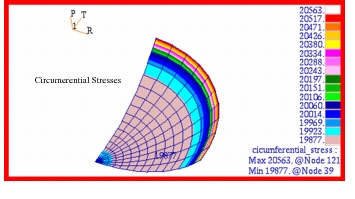
: MSC Nastran Results:
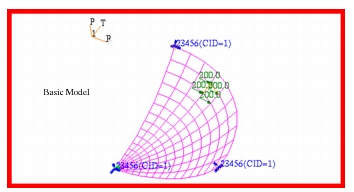
A model of the spherical shell was created using Patran
. Due to symmetry, only one fourth of the shell was modeled with the appropriate axisymmetric boundary conditions applied to the free edges. The model that was created is shown in Figure 14‑32. The majority of the model was meshed with CQUAD4 elements, with the mesh becoming increasingly refined near the center of the shell. Only at the very apex of the shell are CTRIA3 elements used. However, every attempt was made to minimize having high aspect ratio triangular elements that would otherwise cause a loss of accuracy. Using this model, the following results were obtained. Table 14‑17 2D Shell Displacements Source | | | |
max | min |
Theory | .01334 | .01334 | .009433 | .003907 |
MSC Nastran | .01462 | .01383 | .010330 | .003890 |
%, Difference | 9.60% | 3.67% | 9.51% | 0.435% |
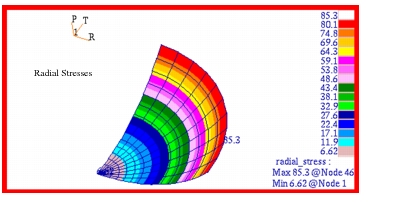
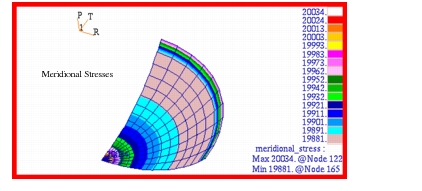
Table 14‑18 Source | | |
max | min | max | min |
Theory | 20,000. | 20,000. | 20,000. | 20,000. |
MSC Nastran | 20,034. | 19,881. | 20,563. | 19,877. |
%, Difference | 0.170% | 0.595% | 2.82% | 0.615% |
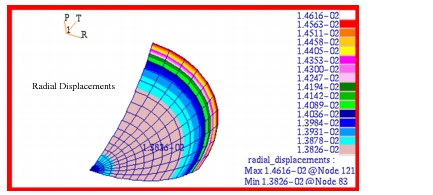
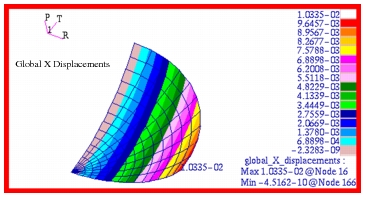
The corresponding fringe plots for the radial displacement and the x-displacement in global coordinates are shown in Figure 14‑33 and Figure 14‑34. The radial displacement plot gives 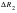 whereas the max value shown on the x-displacement plot corresponds to
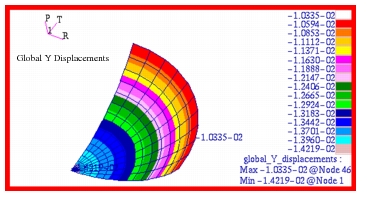
whereas the max value shown on the x-displacement plot corresponds to 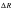 . In Figure 14‑35, the y-displacement in global coordinates is plotted. The difference between the maximum and minimum y-displacements corresponds to
. In Figure 14‑35, the y-displacement in global coordinates is plotted. The difference between the maximum and minimum y-displacements corresponds to 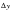 above, or the change in vertical height for the shell. Fringe plots for the radial, meridional and circumferential stresses are shown in Figure 14‑36 through Figure 14‑38. A comparison of the
above, or the change in vertical height for the shell. Fringe plots for the radial, meridional and circumferential stresses are shown in Figure 14‑36 through Figure 14‑38. A comparison of the Patran
fringe plots with the MSC Nastran
results shows an exact correlation between the two. File(s): <install_dir>/results_vv_files/prob005.bdf, prob005.op2
Figure 14‑32 Basic Model of 2D Shell in Spherical Coordinates.
Figure 14‑33 Radial Displacement of Spherical Membrane.
Figure 14‑34 Global Translational X Displacement of Membrane.
Figure 14‑35 Global Translational Y Displacement of Membrane.
Figure 14‑36 Radial Stresses of Spherical Membrane.
Figure 14‑37 Meridional Stresses of Spherical Membrane.
Figure 14‑38 Circumferential Stresses of Spherical Membrane.
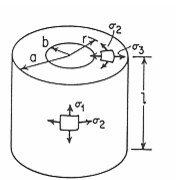
Problem 6: Linear Statics, 2D Axisymmetric Solids
Solution/Element Type:
MSC Nastran, Linear Statics, Solution 101, CTRIAX6 Elements, 2D Axisymmetric Solids
Reference:
Roark, R. J., and Young, W. C., Formulas For Stress and Strain, 5th ed., McGraw-Hill, Inc., 1975, pp. 504-505.
Problem Description:
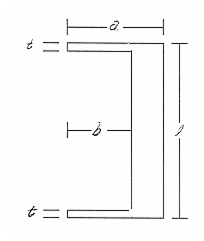
A thick walled cylinder with thick end caps is subjected to a uniform external pressure. Determine both the radial and hoop displacement and stress state at the mid plane of the cylinder.
Engineering Data:
E = 1.0 x 107 psi | |
|
a = 6.0 in |
b = 4.0 in |
l = 11.0 in |
t = 0.5 in |
q = 1000.0 lb/in2 |
Theoretical Solution:
For the case of an externally pressurized thick walled cylinder with thick end caps, there is no closed form solution. The nearest solution corresponds to a capped thick walled cylinder where the restraint afforded by the end caps to radial and hoop contraction is ignored. The presence of the thick end caps would necessarily reduce the radial and hoop displacement at the mid plane of the cylinder, resulting in lower axial and hoop stresses. Only the radial stress would be left unaltered at the mid plane. However, a substantial gradient in all of the stress components should be observed near the ends of the cylinder due to bending of the end caps. Nevertheless, the classical closed form solution is useful in bounding the actual displacements and stresses and is as follows. For the assumed values for 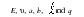 , the following results are obtained for an externally pressurized thick walled cylinder with negligible end caps:
, the following results are obtained for an externally pressurized thick walled cylinder with negligible end caps: MSC Nastran Results:
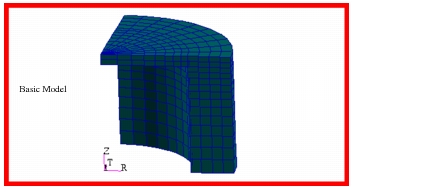
Two models were created with Patran
of the thick walled cylinder. One featured 3 noded and the other 6 noded CTRIAX6 elements. Both models used the same number of elements. The models with the applied loading are shown in Figure 14‑39, which was assumed to be a uniform external ambient pressure of 1000.0 psi. Using these models, results were obtained and the following errors occurred relative to the theoretical values for each of the element topologies that were examined. The results clearly show the expected behavior; namely, the presence of the end caps reduces the inward radial contraction at the center of the cylinder. This necessarily reduces the predicted hoop stress relative to the theoretical value. The only stress components that should correlate with the theoretical values are the radial stress at the ID and OD of the cylinder ad the axial stress at the mean radius of the cylinder.
Table 14‑19 
| 3 Noded CTRIAX | 6 Noded CTRIAX |
r = a | r = b | r = a | r = b |
Theory | -1000.0 | 0.0 | -1000.0 | 0.0 |
MSC Nastran | -903.576 | -268.901 | -1000.697 | -9.847213 |
% Difference | -9.64% | - | 0.0697% | - |
Table 14‑20 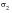
| 3 Noded CTRIAX | 6 Noded CTRIAX |
r = a | r = b | r = a | r = b |
Theory | -2600.0 | -3600.0 | -2600.0 | -3600.0 |
MSC Nastran | -2363.289 | -2967.001 | -2467.246 | -2740.299 |
% Difference | -9.104% | -17.58% | -5.12% | -23.88% |
Table 14‑21 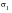
| 3 Noded CTRIAX | 6 Noded CTRIAX |
Theory | -1800.0 | -1800.0 |
MSC Nastran | -1871.255 | -1876.067 |
% Difference | 3.96% | 4.23% |
Table 14‑22 | 3 Noded CTRIAX | 6 Noded CTRIAX |
| | | | | |
Theory | -1.006E-3 | -1.202E-3 | -6.73E-4 | -1.006E-3 | -1.202E-3 | -6.73E-4 |
MSC Nastran | -7.986E-4 | -9.586E-4 | -6.340E-4 | -8.104E-4 | -9.814E-4 | -6.297E-4 |
% Difference | -25.97% | -20.247% | -6.145% | -19.441% | -18.354% | -6.873% |
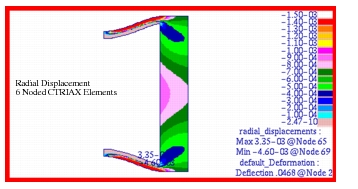
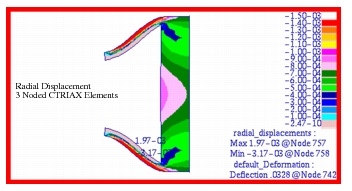
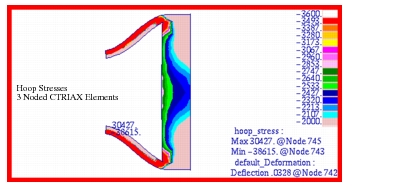
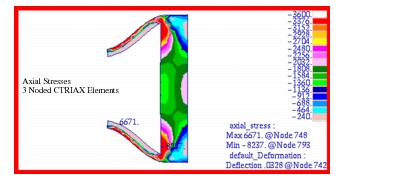
The fringe plots created of the radial displacement are shown in
Figure 14‑40 and
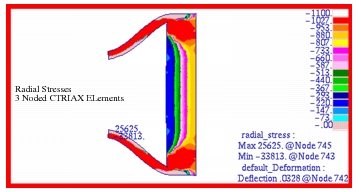
Figure 14‑41. The range has been adjusted to better show the displacement at the center of the cylinder. Similarly, the radial stress distribution is shown in
Figure 14‑42 and
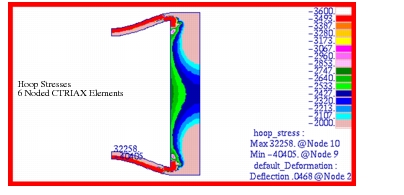
Figure 14‑43; the hoop stress in
Figure 14‑44 and
Figure 14‑45; and the axial stress in
Figure 14‑46 and
Figure 14‑47. A comparison of the Patran fringe plots with the preceding tabular results clearly reveals that the MSC Nastran results are being accurately displayed.
File(s): <install_dir>/results_vv_files/prob006.bdf, prob006.op2
Figure 14‑39 Axisymmetric Models of Thick Walled Cylinder.
Figure 14‑40 Radial Displacement of 6 Noded Axisymmetric Model.
Figure 14‑41 Radial Displacement of 3 Noded Axisymmetric Model.
Figure 14‑42 Radial Stress in 6 Noded Axisymmetric Model.
Figure 14‑43 Radial Stress in 3 Noded Axisymmetric Model.
Figure 14‑44 Hoop Stress in 6 Noded Axisymmetric Model.
Figure 14‑45 Hoop Stress in 3 Noded Axisymmetric Model.
Figure 14‑46 Axial Stress in 6 Noded Axisymmetric Model.
Figure 14‑47 Axial Stress in 3 Noded Axisymmetric Model.
Problem 7: Linear Statics, 3D Solids and Cylindrical Coordinate Frames
Solution/Element Type:
MSC Nastran, Linear Statics, Solution 101, CHEX8 Elements - 3D Solids
Reference:
Roark, R.J., and Young, W. C., Formulas For Stress and Strain, 5th ed., McGraw-Hill, Inc., 1975, pp. 504-505.
Problem Description:
This is a repeat of Problem 6: Linear Statics, 2D Axisymmetric Solids, 42 with the exception that the cylinder and end caps are entirely modeled with MSC Nastran
3D solid HEX8 elements. In addition, all analytical results are recovered in a global cylindrical coordinate frame. This should produce results that are identical to those recovered with CTRIAX6 2D axisymmetric solid elements. Engineering Data:
E = 1.0 x 107 psi | |
|
a = 6.0 in |
b = 4.0 in |
l = 11.0 in |
t = 0.5 in |
q = 1000.0 psi |
Theoretical Solution:
MSC Nastran Results:
A model was created of the thick walled cylinder with the end caps using just MSC Nastran
3D solid CHEX8 elements. Due to symmetry, only one eighth of the cylinder was modeled, with the appropriate axisymmetric and symmetry boundary conditions applied to the free faces of the model. The model that was created is shown in Figure 14‑48 and the applied boundary conditions in Figure 14‑49. Using this model, the results below were computed at the middle of the cylinder. Once again, the analytical results demonstrate the expected behavior. Namely, the presence of the end caps reduces the inward radial contraction at the center of the cylinder. This reduces the predicted hoop stress relative to the theoretical value. The only stress components that are unaffected are the radial stress at the ID and OD of the cylinder and the axial stress at the mean radius of the cylinder. The percent error that occurred relative to the theoretical values for the radial and axial stress are shown below. For comparative purposes, the results that were obtained for a three noded CTRIAX6 element have been included, illustrating the excellent degree of correlation that exists when using either element type to model axisymmetric structures.
Table 14‑23 Radial Stress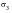
| CHEX8 | CTRIAX6, 3 Noded |
r = a | r = b | r = a | r = b |
Theory | -1000.0 | 0.0 | -1000.0 | 0.0 |
MSC Nastran | -918.731 | -184.862 | -903.576 | -268.901 |
% Difference | -8.13% | - | -9.64% | - |
Table 14‑24 Hoop Stress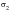
| CHEX8 | CTRIAX6, 3 Noded |
r = a | r = b | r = a | r = b |
Theory | -2600.0 | -3600.0 | -2600.0 | -3600.0 |
MSC Nastran | -2902.487 | -2418.523 | -2467.246 | -2740.299 |
% Difference | 11.634% | -32.819% | -5.12% | -23.88% |
Table 14‑25 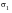
| CHEX8 | CTRIAX6, 3 Noded |
Theory | -1800.0 | 1800.0 |
MSC Nastran | -1760.235 | 1871.255 |
% Difference | -2.21% | 3.96% |
Table 14‑26 | CHEX8 | CTRIAX6 |
| | | | | |
Theory | -1.006E-3 | -1.202E-3 | -6.73E-4 | -1.006E-3 | -1.202E-3 | -6.73E-4 |
MSC Nastran | -8.095E-4 | -9.980E-4 | -6.043E-4 | -8.104E-4 | -9.814E-4 | -6.297E-4 |
% Difference | -19.535% | -18.346% | -10.212% | -19.441% | -18.354% | -6.873% |
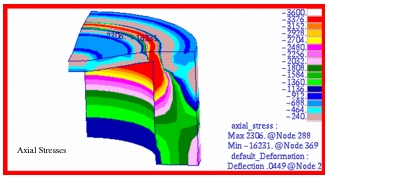
The corresponding fringe plots that were generated for the radial and axial displacement are shown in Figure 14‑50 and Figure 14‑51. Similarly, fringe plots for the radial, hoop and axial stress are shown in Figure 14‑52, Figure 14‑53, and Figure 14‑54, respectively. In each of the fringe plots, the range has been purposely adjusted to better show the gradient in displacement and stress that exists at the middle of the cylinder. In addition, all stresses and displacements have been transformed to a cylindrical coordinate frame. If the boundary conditions were properly applied, then an axisymmetric response should be present, which is evident in each of fringe plots. File(s): <install_dir>/results_vv_files/prob007.bdf, prob007.op2
Figure 14‑48 Solid Model of Thick Walled Cylinder with End Caps.
Figure 14‑49 Loads and Boundary Conditions of Cylinder.
Figure 14‑50 Radial Displacements of Thick Walled Cylinder.
Figure 14‑51 Axial Displacement of Thick Walled Cylinder.
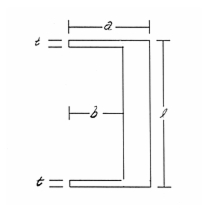
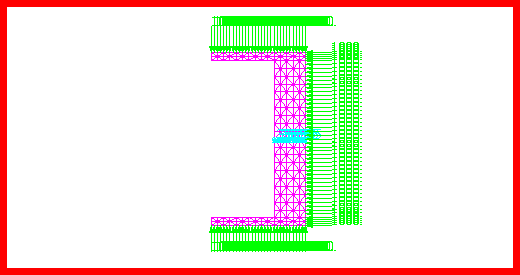
Problem 8: Linear Statics, Pinned Truss Analysis
Solution/Element Type:
MSC Nastran, Linear Statics, Solution 101, CROD 1D Elements.
Reference:
Przemieniecki, J.S., Theory of Matrix Structural Analysis, McGraw-Hill, Inc., 1968, p. 155.
Problem Description:
A pinned joint truss is loaded with a force at one end and one of the components is heated uniformly to an elevated temperature. Considering thermal effects, find the displacements of the truss joints and the forces and stresses in each of the axial elements.
Engineering Data:
Theoretical Solution:
The theoretical solution was calculated by using the matrix equation on page 159 of the reference using the values listed above for  . The results are as follo
. The results are as follows:
Displacements:
Element Forces:
| |
P1 = -636.36 lb (compression) | P4 = -514.25 lb (compression) |
P2 = +899.95 lb (tension) | P5 = +363.64 lb (tension) |
P3 = +363.64 lb (tension) | P6 = 0. lb |
Element Stresses:
MSC Nastran Results:
Due to the pinned construction of the truss, all members are only capable of carrying axial loads. This necessitated that the truss be modeled using MSC Nastran
1D CROD elements. The model that was created using Patran
is shown in Figure 14‑55. Note that each truss member was modeled using a single CROD element. The loads and boundary conditions that were applied to the model are also shown in Figure 14‑55. The following results were obtained with MSC Nastran.
Table 14‑27 Displacements | u1 | v1 | u2 | v2 |
Theory | -1.272727x10-3 | +6.363636x10-3 | +7.272727x10-4 | +3.636364x10-3 |
MSC Nastran | -1.272727x10-3 | +6.363636x10-3 | +7.272727x10-4 | +3.636364x10-3 |
% Difference | 0.0% | 0.0% | 0.0% | 0.0% |
Table 14‑28 | P1 | P2 | P3 | P4 | P5 | P6 |
Theory | -636.36 | +899.95 | +363.64 | -514.26 | +363.64 | 0. |
MSC Nastran | -636.36 | +899.95 | +363.64 | -514.26 | +363.64 | 0. |
% Difference | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
Table 14‑29 | | | | | | |
Theory | -636.36 | +1272.73 | +363.64 | -727.27 | +363.64 | 0. |
MSC Nastran | -636.36 | +1272.73 | +363.64 | -727.27 | +363.64 | 0. |
% Difference | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
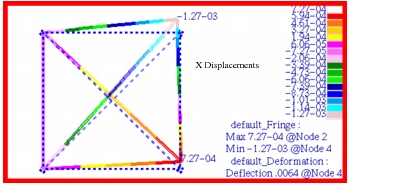
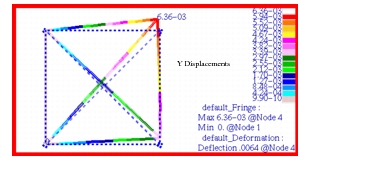
The corresponding color fringe plots that were made in Patran
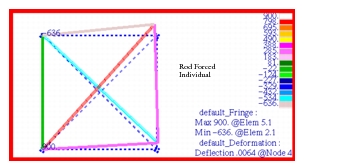
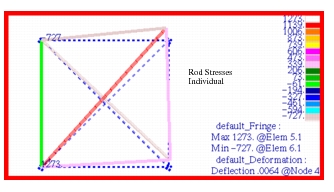
of the x- and y-components of displacement are shown in Figure 14‑56 and Figure 14‑57, respectively. For the purposes of these plots, the target entity was set to nodes and the averaging domain was specified as all entities. The rod forces and stresses that were predicted by MSC Nastran
are shown in Figure 14‑58 and Figure 14‑59, respectively. Unlike displacements, it was necessary to set the target entity to elements and the averaging domain to individual. This avoided having any averaging across adjacent elements which otherwise would have given an inaccurate representation of the actual results. A closer inspection of these plots reveals that the results that are being shown are in fact identical to those predicted by MSC Nastran
. File(s): <install_dir>/results_vv_files/prob008.bdf, prob008.op2
Figure 14‑55 Basic Pinned Truss Analysis Model.
Figure 14‑56 X Translational Displacement of Pinned Truss.
Figure 14‑57 Y Translational Displacement of Pinned Truss.
Figure 14‑58 Rod Forces from Pinned Truss Analysis.
Figure 14‑59 Axial Stresses from Pinned Truss Analysis.
Problem 9: Nonlinear Statics, Large Deflection Effects
Solution/Element Type:
MSC Nastran, Nonlinear Statics, Solution 106, Shell Element with Standard Formulation, CQUAD4 and CQUAD8
Reference:
Timoshenko, S., and Woinowsky-Krieger, S., Theory of Plates and Shells, McGraw-Hill, Inc., 1959, p. 422.
Problem Description:
A square plate with clamped edges is loaded uniformly such that the center deflection exceeds the plate thickness. Considering large deflection effects (small strain theory), find the deflection at the center of the plate.
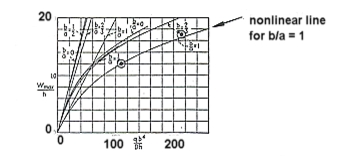
Theoretical Solution:
The following diagram summarizes the theoretical solution for the case when large deflection effects are both considered and ignored.
For
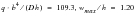
, with nonlinear effects.
For
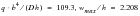
, without nonlinear effects.
MSC Nastran Results:
Due to symmetry, only one-fourth of the plate was modeled. The outer edges were fully restrained while the appropriate symmetry boundary conditions were imposed along the remaining free edges and at the center of the plate. Two models were created. The first was meshed with MSC Nastran CQUAD4 elements which have a finite strain formulation needed to incorporate large deflection effects. The second model was meshed with CQUAD8 elements, which do not have a finite strain formulation. Both models along with the applied loading and imposed boundary conditions are shown in
Figure 14‑60 and
Figure 14‑61. The MSC Nastran results that were obtained are summarized below and plotted in
Figure 14‑62 and
Figure 14‑63.
Table 14‑30 Element Type | 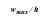 , (Theory) | 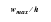 , (MSC Nastran) | % Difference |
QUAD4 | 1.20 | 1.26 | 5.0% |
QUAD8 | 2.208 | 2.21 | .091% |
It should be noted that although both analyses were conducted using MSC Nastran, Solution 106 with large deflection effects included, the analysis performed with CQUAD8 excluded any geometric nonlinearities since this type of element has no finite strain formulation. This illustrates the care that must be exercised when performing a nonlinear statics analysis with mixed element types. The same problem exists for CTRIA3 and CTRIA6 elements.
File(s): <install_dir>/results_vv_files/prob009_Q4.bdf, prob009_Q4.op2, prob009_Q8.bdf, prob009_Q9.op2, prob009_T3.bdf, prob009_T3.op2, prob009_T6.bdf, prob009_T6.op2
Figure 14‑60 CQUAD4 Model of Plate with Loads and BCs.
Figure 14‑61 CQUAD4 Model of Plate with Loads and BCs.
Figure 14‑62 Large Deflection Displacements of CQUAD4 Model.
Figure 14‑63 Large Deflection Displacements of CQUAD8 Model.
Problem 10: Linear Statics, Thermal Stress with Solids
Solution/Element Type:
MSC Nastran, Linear Statics, Solution 101, Solid Elements With Standard Formulation, CHEXA (8 and 20 noded), CPENTA (6 and 15 noded), CTETRA (4 and 10 noded).
Reference:
Timoshenko, S., and Goodier, J. N., Theory of Elasticity, 2nd ed., McGraw-Hill, Inc., 1951, pp. 401-403.
Problem Description:
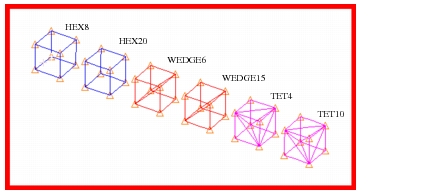
Six cubes are subjected to three independent linear temperature gradients in the
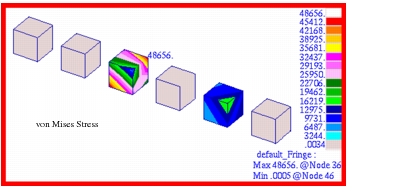
x-, y- and z- directions. The cubes are meshed with either HEX8, HEX20, WEDGE6, WEDGE15, TET4 or TET10 elements. Each cube is mounted on a weak elastic foundation so that the resultant thermal expansion is unrestrained. Compute the Von Mises stress in each of the cubes.
Theoretical Solution:
In general, when the applied temperature is a linear function of x, y and z, the strain induced by free thermal expansion is:
The corresponding stress-strain relationships for three dimensional problems are:
Equations (c) are not affected by temperature since free thermal expansion does not produce angular distortion in an isotropic material. The remaining stress-strain relationships given by equations (b) can only be satisfied after substitution of the strains due to free thermal expansion if
Thus, a linear temperature gradient should produce no apparent stress, provided the expansion is completely unrestrained.
MSC Nastran Results:
To demonstrate that thermal stress effects can be properly recovered for all of the various solid element topologies supported by MSC Nastran
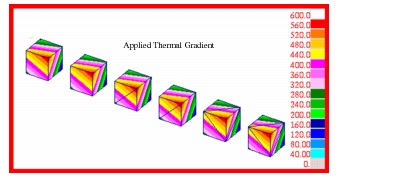
, a simple model was created that consisted of 6 cubes. Each cube was subjected to three independent linear temperature gradients of 100, 200 and 300 degrees F per inch along the x, y and z axes, respectively. The cubes were meshed with either HEX8, HEX20, WEDGE6, WEDGE15 TET4 or TET10 elements with a mesh density of one element per edge. The model that was created is shown in Figure 14‑64 and the applied temperatures are shown in Figure 14‑65. Due to the presence of three simultaneous temperature gradients, the faces of the cubes will not remain planar. This precludes applying uniform constraints along any face of the cubes in order to prevent any rigid body translation from occurring. Instead every vertex of a cube was attached to a triad of three weak grounded springs that were aligned in either the x, y or z-directions. Each spring had a spring rate of 0.1 lbs / inch, which would provide minimal resistance to thermal expansion. This should generate only a minimal amount of residual stress in each of the cubes.
The maximum von Mises stress that was computed by MSC Nastran for a given element topology are summarized below.
Table 14‑31 Element Type | Max Von Mises Stress (psi) |
HEX8 | .001512 |
HEX20 | .007403 |
WEDGE6 | 49811 |
WEDGE15 | .007900 |
TET4 | 7610 |
TET10 | .005904 |
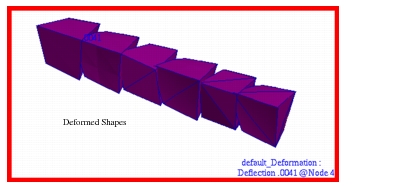
The corresponding deformed shapes and von Mises stress contours that were generated using Patran are shown in
Figure 14‑66 and
Figure 14‑67, clearly showing the high residual stresses that were generated in both the degenerate WEDGE6 and TET4 elements. The peak values for the von Mises stress shown are somewhat less than those shown in due to the nodal averaging of results at adjacent elements.
Ideally, the presence of a weak elastic support should have provided minimal restraint to thermal expansion, resulting in a near zero stress state. This behavior was observed in both the HEX8 and HEX20 elements as well as the higher order TET10 and WEDGE15 elements. The extremely high stresses observed with TET4 and WEDGE6 elements would not be unexpected since these elements tend to be excessively stiff resulting in a loss of accuracy. Consequently, the results illustrate the care that must be exercised when modeling with the solids and the need to avoid excessive use of degenerate elements, especially in areas where high stress gradients are predicted to occur, such as at the vertices of the cubes in this particular problem.
File(s): <install_dir>/results_vv_files/prob010.bdf, prob010.op2
Figure 14‑64 Models of Different Solid Element Types.
Figure 14‑65 Thermal Gradient Applied to Solid Elements.
Figure 14‑66 Deformed Shape of Elements Due to Thermal Gradient.
Figure 14‑67 von Mises Stress in Elements due to Thermal Gradient.
Problem 11: Superposition of Linear Static Results
Solution/Element Type:
MSC Nastran, Linear Statics, Solution 101, Simple Shell Elements, CQUAD4 and CTRIA3
Reference:
Ugural, A.C., Stresses in Plates and Shells, McGraw-Hill, Inc., 1981, pp. 41-42.
Roark, R.J., and Young, W.C., Formulas For Stress and Strain, 5th ed., McGraw-Hill, Inc., 1975, p. 338.
Problem Description:
A flat annular plate is subjected to a uniform pressure. The inner edge is free and the outer edge simply supported. Determine the maximum deflection of the plate.
Theoretical Solution:
The resultant deformation for a simply supported annular plate can be derived by summing the deformations obtained for a flat circular plate subjected to the same pressure load, an annular plate carrying along its inner edge a shear force per unit circumferential length of 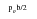
and an annular plate with a distributed radial bending moment of
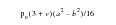
. All of the plates have the same outer radius and the both annular plates have the same inner radius.
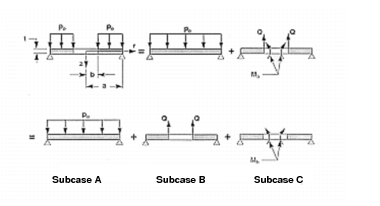
According to reference (2), the maximum deflection occurs at the inner radius and is given by the expression:
(14‑1)
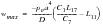
body
(14‑2)
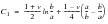
(14‑3)
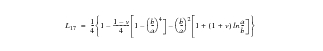
(14‑4)
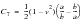
(14‑5)
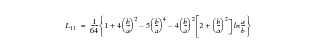
(14‑6)
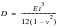
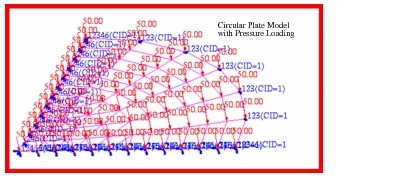
For the purposes of this problem, models of a flat circular and annular plates where created in Patran using the following dimensions, applied loading and material properties:
MSC Nastran Results:
The model that was generated for a uniformly pressurized circular plate is shown in
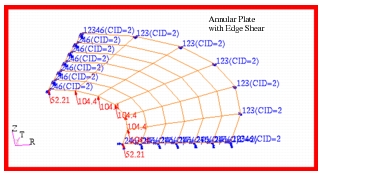
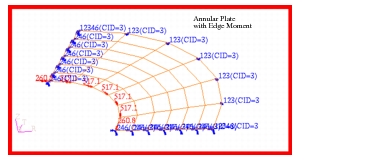
Figure 14‑68. Due to symmetry, only a 90 degree sector of the plate was modeled with axisymmetric boundary conditions being applied along the lateral edges of the sector. The center of the plate was constrained to move only in the vertical direction. Between the inner and outer radius of the annular plate, a mesh consisting of CQUAD4 elements was used to maximize accuracy. Conversely, inboard of the inner radius, a CTRIA3 mesh was used to avoid having badly distorted CQUAD4 elements that might otherwise result in a loss of accuracy. By having the mesh transition coincide exactly with the edges of the annular plate, this permitted using a single model to investigate the behavior of a complete circular plate as well as an annular plate, with the elements corresponding to just the annular and the complete plate being assigned to a different groups within Patran. The corresponding models that were used to investigate the case of an annular plate subjected to either a distributed edge shear or moment are shown in
Figure 14‑69 and
Figure 14‑70.
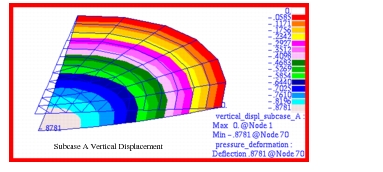
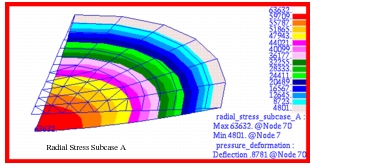
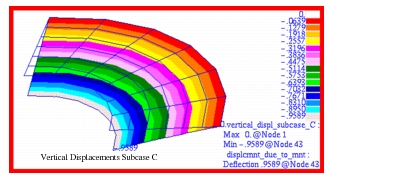
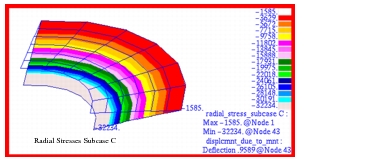
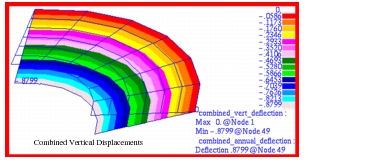
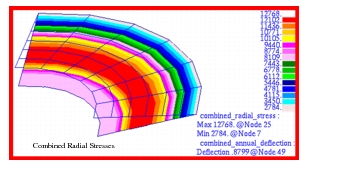
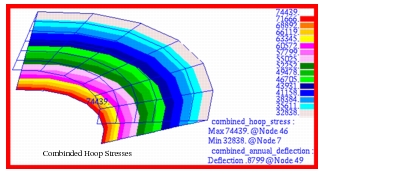
Due to axisymmetric response of the plate, all deformations are principally confined to the vertical, or z-direction. The resultant vertical displacements as well as the hoop and radial stresses that were computed for each of the three different subcases are shown in Figure 14‑71 through Figure 14‑79. The displacement and stress contours have been superimposed upon an exaggerated deformed shape. The resultant displacements and stresses that were derived by combining the results from each of the separate subcases are shown in Figure 14‑80 though Figure 14‑82. An examination of Figure 14‑80 indicates that a maximum deformation of -0.8799 inches occurs at the inner radius of a flat annular plate subjected to a uniform pressure of 50 psi. Note that for the combined stress plots, the averaging was set to Target Entities to remove the influence of the stresses from the CTRIA3 elements. Substitution of the model parameters into equations
(14‑1) through
(14‑6) yields a maximum deflection at the inner radius of
The value derived within Patran was -.8799 in, or a deviation of approximately 0.69% from the theoretical value
File(s): <install_dir>/results_vv_files/prob011_A.bdf, prob011_A.op2, prob011_B.bdf, prob011_B.op2, prob011_C.bdf, prob011_C.op2
Figure 14‑68 Model of Pressurized Circular Plate (Subcase A).
Figure 14‑69 Annular Plate with Edge Shear (Subcase B).
Figure 14‑70 Annular Plate with Edge Moment (Subcase C).
Figure 14‑71 Vertical Displacement of Circular Plate (Subcase A).
Figure 14‑72 Radial Stress of Circular Plate (Subcase A).
Figure 14‑73 Hoop Stress of Circular Plate (Subcase A).
Figure 14‑74 Vertical Displacement of Annular Plate (Subcase B).
Figure 14‑75 Radial Stress of Annular Plate (Subcase B).
Figure 14‑76 Hoop Stress of Annular Plate (Subcase B).
Figure 14‑77 Vertical Displacement of Annular Plate (Subcase C).
Figure 14‑78 Radial Stress of Annular Plate (Subcase C).
Figure 14‑79 Hoop Stress of Annular Plate (Subcase C).
Figure 14‑80 Combined Vertical Displacements of Annular Plate.
Figure 14‑81 Combined Radial Stress of Annular Plate.
Figure 14‑82 Combined Hoop Stress of Annular Plate.
Problem 12: Nonlinear Statics, Post-Buckled Column
Solution/Element Type:
MSC Nastran, Nonlinear Statics, Solution 106, CBEAM, 1D Beams with Standard Formulation.
Reference:
Timoshenko, S. P., and Gere, J. M., Theory of Elastic Stability, McGraw-Hill, Inc., 1961, p. 48.
Problem Description:
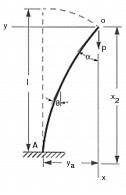
Find the displaced position of a post-buckled column, fixed at one end with an applied axial load at the other end.
Engineering Data:
Theoretical Solution:
: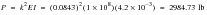
where:
MSC Nastran Results:
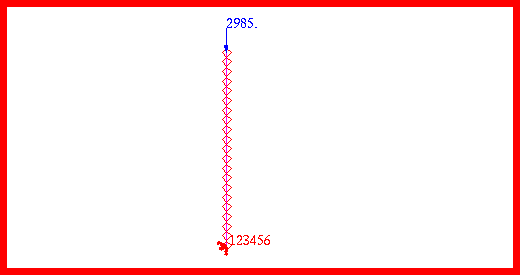
To determine the post-buckled shape for the beam, the model shown in Figure 14‑83 was generated using Patran
. The model consisted of 20 1D CBEAM elements that used a standard generalized formulation. To ensure that the beam will deflect laterally, a slight horizontal load was applied to the beam in addition to an axial load of 2984.73 lbs. In this case a lateral load of 10 lbs was used. In addition, since the structure is post-buckled, it is inherently unstable. This requires that the user set the MSC Nastran
parameter TESTNEG to -2 in the input file. The following results were obtained with MSC Nastran.
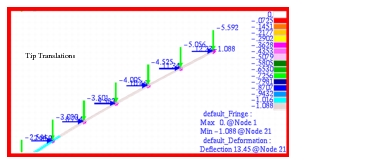
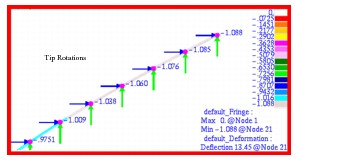
Table 14‑32 Source | | | |
MSC Nastran | 14.4076 | 12.2275 | 62.3583 o |
Theory | 14.8161 | 11.8624 | 60.0 o |
%, Difference | -2.7571% | 3.0778% | 3.9305% |
The corresponding Patran
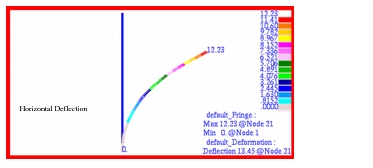
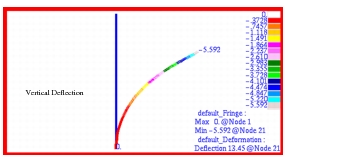
fringe plots that were made of the horizontal and vertical displacements are shown in Figure 14‑84 through Figure 14‑85. Deflection plots were set to True Scale as opposed to a percentage of the model. The rotation about the global z-axis given in radians is shown in Figure 14‑86. For the purposes of evaluating the accuracy of these plots, it is necessary to use the following conversions: where 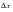 and
and 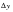 are the
are the MSC Nastran
horizontal and vertical nodal displacements, respectively. Vector plots of the translational and rotational displacements are shown in Figure 14‑87 and Figure 14‑88. After making the appropriate conversions, it is apparent that the Patran
results are identical to those obtained with MSC Nastran
. File(s): <install_dir>/results_vv_files/prob012.bdf, prob012.op2
Figure 14‑83 Nonlinear Beam Post-Buckling Model.
Figure 14‑84 Post-Buckled Horizontal Deformation of Beam.
Figure 14‑85 Post-Buckled Vertical Deformation of Beam.
Figure 14‑86 Post-Buckled Rotational Deformation about Z of Beam.
Figure 14‑87 Vector Plot of Tip Deflections of Beam.
Figure 14‑88 Vector Plot of Rotational Deformation of Beam.