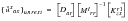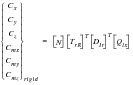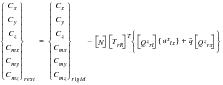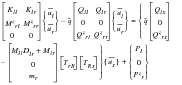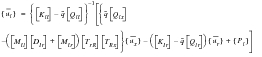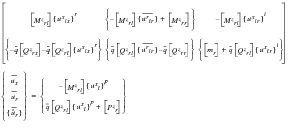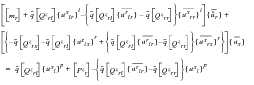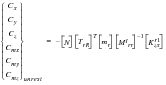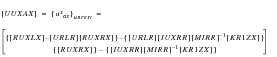XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> Aeroelastic Solutions
The equations of the preceding section can now be solved once we have introduced two new concepts. The first concept is “restrained” vs. “unrestrained” and refers to how the displacements of supported degrees of freedom (ur in the previous section) are treated. The Restrained approach sets these terms to zero and then solves for the remaining variables. This provides considerable simplification in the equations to be solved and is equivalent to the type of analysis that would be performed in a flight simulator. The Unrestrained approach applies a mean axis constraint (see Unrestrained Analysis below) to solve for ur that is orthogonal to the rigid body motions of the vehicle. This corresponds to the equations of a free-flying vehicle and is therefore equivalent to the type of analysis that would be performed in a flight test. MSC.Nastran uses the restrained formulation for the majority of its calculations, but also does unrestrained calculations for the computation of stability derivatives and flexible load increments.
The second concept is that of Unit Loads and Solutions. The static aeroelastic capability implemented in the first release of FlightLoads is linear so that the total solutions can be regarded as the summation of unit solutions that are obtained from applying a unit value to a particular aerodynamic extra point (component of the u
x vector.). FlightLoads exploits this property in arriving at the overall solutions, in creating data through the Flexible Increment Method of
Aeroelasticity and in subsequently presenting the data to the user through
Results Browser. This section makes a distinction between Unit Loads/Solutions that are due to inertia loads and those that are due to other rigid body motions, such as angle of attack or control surface motion. The GUI of main body of this report does not distinguish between these two types of loads, but does distinguish between flexible, rigid and total loads (where “rigid” is the aerodynamic load applied to the structure, “flexible” is the incremental load due to the aeroelastic deformation and “total” is the sum of the two).
Restrained Analysis (Displacements Relative to
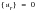
)
We can rewrite
(E‑4) to enable solution of the free-free equations by combining
(E‑4) with
(E‑13) and using
(E‑14) to relate the (rigid body) l-set accelerations to the r-set accelerations (under the usual assumption of quasi-static analysis) to obtain:
(E‑16)
Following the derivation of Eq. 2-69 of Ref. 12, we premultiply the first equation by
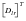
and add it to the second to obtain:
(E‑17)
in which the superscript “z” has been used to denote the r-set reductions:
(E‑18)
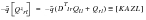
(E‑19)
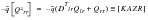
(E‑20)
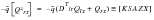
(E‑21)
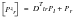
we have also applied the relationships that
by the definition of the rigid body transformation matrix and:
This latter term is the definition of the "reduced mass matrix." Solving the first equation for
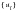
in terms of
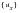
(noting that
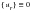
):
(E‑22)
Looking at
(E‑22), we can rewrite it in terms of three component “unit solutions”:
(E‑23)
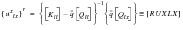
(E‑24)
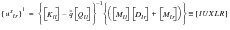
(E‑25)
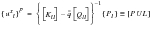
where the r, i and p superscripts denote rigid forces, inertial forces and static forces, respectively. Due to the Boolean matrix selection of the acceleration parameters and the fact that the rigid aerodynamics produces no forces for unit accelerations, the rigid and inertial unit solution vectors are either zero or nonzero for any parameter. This union of elastic unit solutions is denoted:
(E‑26)
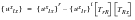
Using these relations leads to a simplified form of
(E‑22):
(E‑27)
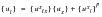
In this form, we can see that the first term is the deflection due to the aeroelastically corrected rigid aerodynamic loads and inertial forces and the second is the deflection due to the aeroelastically corrected statically applied load.
Substituting
(E‑27) into the second row of , results in the following relation that is the equivalent of Eq. 2-74 of Ref. 12 (ZZX * UX = PZ).
(E‑28)
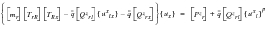
There is one equation for every supported degree of freedom and the unknowns are the free parameters in
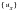
. Note that the right hand side is zero unless there are statically applied loads.
Restrained Stability Derivatives from the Unit Solutions
By inspection of
(E‑28), we can see that the rigid (splined) stability derivatives in the reference coordinate system are:
(E‑29)
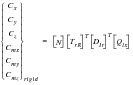
where
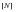
matrix is the normalization matrix that is derived from the user input reference areas and lengths as:
(E‑30)

Similarly, the elastically corrected stability derivatives are:
(E‑31)
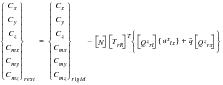
Unrestrained Analysis and Stability Derivatives (Displacements Relative to Mean Axis)
In addition to the restrained analysis (trim and stability derivative calculation), MSC.Nastran computes the unrestrained stability derivatives: force increments due to unit perturbations about the mean axes. To introduce the mean axes, an orthogonality criterion is applied such that the rigid body motions are orthogonal to the elastic deflections:
(E‑32)
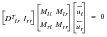
where we introduce the overbar to denote deflections in the mean axis system. These equations are added to those of to yield:
(E‑33)
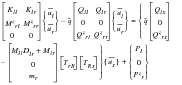
where we again use the “z” superscript:
(E‑34)
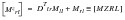
(E‑35)
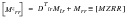
Again, solving the first equation for
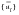
in term of
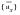
(noting that
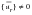
):
(E‑36)
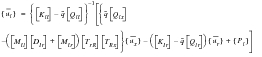
Looking at
(E‑36), we can rewrite it in terms of the three component “unit solutions” of the restrained case and an additional term due to the rigid body displacements:
(E‑37)
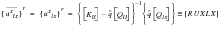
(E‑38)
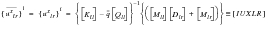
(E‑39)
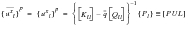
(E‑40)
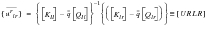
where the r, i and p superscripts again denote rigid forces, inertial forces and static forces, respectively.
Using these relations leads (using the combination of elastic unit solutions of
(E‑26)) to a simplified form of
(E‑36):
(E‑41)
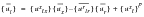
In this form, we can see that we have added a term to the restrained solution due to the “elastically corrected” rigid body motion of the support points.
Substituting
(E‑41) into the second and third rows of
(E‑33), and keeping the accelerations of the support points
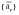
separate from their
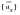
counterparts we obtain:
(E‑42)
Using the first equation to solve for
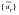
in terms of
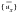
and
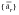
, we obtain:
(E‑43)
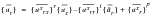
(E‑44)
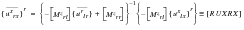
(E‑45)
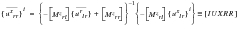
and
(E‑46)
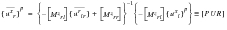
Substituting
(E‑43) into the second equation of
(E‑42) leads to trim equation:
(E‑47)
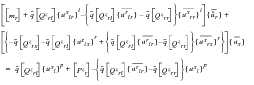
which we can solve for
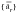
in terms of
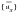
if we ignore the static load (which does not participate in the stability derivative calculation. Then, if we premultiply the resultant accelerations by the total mass matrix
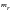
, we have the forces resulting from unit perturbation of the trim parameters: the stability derivatives. To solve, we define the intermediate quantities:
(E‑48)
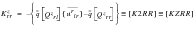
(E‑49)
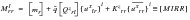
(E‑50)
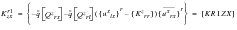
The accelerations of the r-set due to the trim parameters are then
(E‑51)
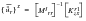
Then, the dimensional unrestrained stability derivatives can be computed as:
(E‑52)
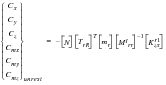
Recovery of Unit Solutions to the a-set and to the k-set
To compute the distributed force increments, we need to recover the unit solutions. Each displacement has a component due to the rigid aerodynamic forces and a component due to the accelerations. Using the previous development, we can summarize the l-set and r-set components as shown in
Table E‑1.
To obtain the total elastic increment displacements, the sums of the rigid and inertial increments must be obtained using
(E‑26) for the restrained case and using the combination of
(E‑41) and
(E‑43) for the unrestrained case. Note that, in this formulation, the inertial increment is always
subtracted from the rigid increment.
Table E‑1 Component | Due to Rigid Forces | Due to Inertial Forces |
Restrained  | | |
Restrained 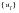 | | |
Unrestrained 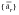 | | |
Unrestrained 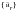 | | |
Unrestrained 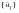 | | |
Recovery of these displacements to the a-set involves only the merging of the r-set and l-set partitions. To give names to these a-set data:
(E‑53)
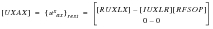
(E‑54)
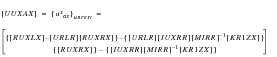
where the rigid increment and inertial increment are shown separately with the appropriate sign. These displacement fields are the basic data needed to compute the increments in force due to the elastic response of the aircraft.
To obtain the same data in the k-set, the displacement spline relationship can be applied to each of the displacement fields. In the a-set, this is
(E‑55)
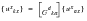
where
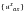
represents the appropriate displacement field (rigid or inertial, restrained or unrestrained).
Distributed Force Increments from Unit Solutions
For purposes of aircraft simulation, it is useful to have the distributed forces for each of the aerodynamic extra points that integrate to the stability derivatives. These data can be used to perform incremental bending moment, shear and torque calculations for a particular set of trim parameters (
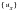
or
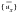
as appropriate). The rigid forces are trivially computed from:
(E‑56)
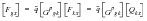
To obtain the rigid forces and force increments from the unit solutions one uses the forces due to the unit solution’s displacements using the usual relationship:
(E‑57)
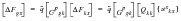
where the displacement field(s) due to the perturbations
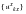
are simply the unit solutions of
Table E‑1 recovered to the k-set.
Inertial Forces: The basic inertial forces (that is, those from the rigid airplane) are needed, since the terms in
Table E‑1 represent only the aeroelastic increments due to the displacements caused by the inertial forces. The structural inertial force increments are computed directly from:
(E‑58)

where the incremental accelerations
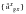
are computed by recovering the a-set incremental accelerations to the g-set in the usual manner. The a-set incremental accelerations are computed from:
(E‑59)
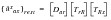
for the restrained case in which
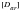
is computed by merging
with an identity matrix over the r-set. For the unrestrained case, the r-set accelerations come from
(E‑51) and the a-set accelerations are then:
(E‑60)