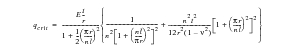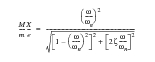XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX''"> Verification and Validation
- Problem 13: Nonlinear Statics, Beams with Gap Elements
- Problem 14: Normal Modes, Point Masses and Linear Springs
- Problem 15: Normal Modes, Shells and Cylindrical Coordinates
- Problem 16: Normal Modes, Pshells and Cylindrical Coordinates
- Problem 17: Buckling, shells and Cylindrical Coordinates
- Problem 18: Buckling, Flat Plates
- Problem 19: Direct Transient Response, Solids and Cylindrical Coordinates
- Problem 20:Modal Transient Response with Guyan Reduction and Bars, Springs, Concentrated Masses and Rigid Body Elements
- Problem 21: Direct Nonlinear Transient, Stress Wave Propagation with 1D Elements
- Problem 22: Direct Nonlinear Transient, Impact with 1D, Concentrated Mass and Gap Elements
- Problem 23: Direct Frequency Response, Eccentric Rotating Mass with Variable Damping
- Problem 24: Modal Frequency Response, Enforced Base Motion with Modal Damping and Rigid Body Elements
- Problem 25:Modal Frequency Response, Enforced Base Motion with Modal Damping and Shell P-Elements
- Problem 26: Complex Modes, Direct Method
- Problem 27: Steady State Heat Transfer, Multiple Cavity Enclosure Radiation
- Problem 28: Transient Heat Transfer with Phase Change
- Problem 29: Steady State Heat Transfer, 1D Conduction and Convection
- Problem 30: Freebody Loads, Pinned Truss Analysis
Problem 13: Nonlinear Statics, Beams with Gap Elements
Solution Type:
MSC Nastran, Nonlinear Statics, Solution 106. Normal Modes, CBEAM and CGAP
Reference:
McCormac, J.C., Structural Analysis, 3rd ed., New York: Intext Educational Publishers, 1975, p. 323, ex. 17.12.
Problem Description:
A simply supported beam is hinged at one end and supported by lifting rollers at two other locations. Allowing for lift-off to occur, determine the vertical deflections under the load points.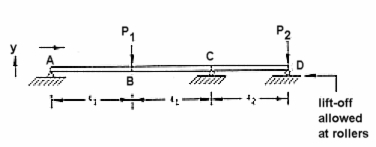
Engineering Data:
Theoretical Solution:
(Lift-off occurs at point D only)
MSC Nastran Results:
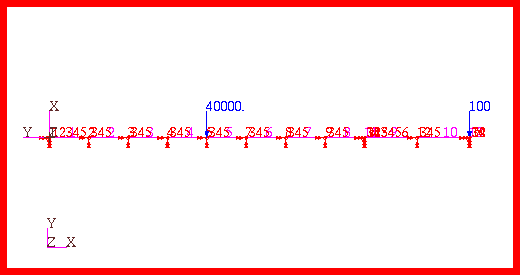
To compute the vertical displacement at the load points, the model shown in Figure 14‑1 was generated using Patran
. This model consisted of 13 CBEAM elements as well as two CGAP elements that were used to model the roller supports at points C and D. Since the CGAP elements had zero length, an additional coordinate frame, shown at the left end of the model, was used to define the orientation for both CGAP elements. In addition, both CGAP elements were provided a high closed stiffness, but no open stiffness. In this way the beam could lift-off the roller supports. Using this model, the following vertical displacements were calculated at both load points: Table 14‑1 Vertical Deflection of Beam with Lift-OffSource | | |
MSC Nastran | -1.01 | +0.546 |
Theory | -1.01 | +0.544 |
%, Difference | 0.0% | 0.366% |
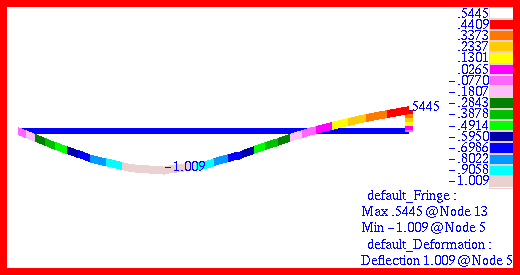
The corresponding fringe plot that was made of the displacements with Patran
is shown in Figure 14‑2. Here the fringe plot for displacements has been superimposed upon an exaggerated deformation plot. In addition, the maximum and minimum values for the vertical displacements are shown at the nodes where they occur. These values are clearly identical to the MSC Nastran
results. File(s): <install_dir>/results_vv_files/prob012.bdf, prob012.op2
Figure 14‑1 Model of Non-Linear Gap Problems with Lift-off.
Figure 14‑2 Deflection Plot of Lift-off of Beam.
Problem 14: Normal Modes, Point Masses and Linear Springs
Solution/Element Type:
MSC Nastran, Normal Modes, Solution 103, CONM2 and CELAS1 Elements.
Reference:
Blevins, R.D., Formulas For Natural Frequency and Mode Shape, Kreiger Publishing Co., 1984, p. 50.
Problem Description:
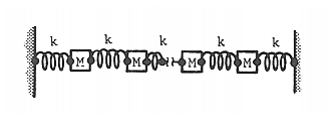
Four equal masses are linked by five equal springs. Assuming that all motion is confined to the linear axis of the springs, determine the natural frequencies for the first four modes.
Engineering Data
:
Theoretical Solution:
For a system consisting of four equal masses and five springs, the natural frequencies of and mode are given by the equations below. Substituting in the values for the mass and spring constants yields the following natural frequencies for the first four mode shapes:
MSC Nastran Results:
To compute the natural frequencies for the spring-mass system, the model shown in
Figure 14‑3 was generated using Patran. The masses were modeled using CONM2 point mass elements while the springs were modeled with linear elastic CELAS1 elements. All motion was restricted to the x-, or axial, direction. The opposing ends of the model were fixed. The following results were computed:
Table 14‑2 Natural Frequencies, HertzSource | | | | |
MSC Nastran | 0.6955 | 1.3230 | 1.8209 | 2.1406 |
Theory | 0.6955 | 1.3230 | 1.8209 | 2.1406 |
%, Difference | 0.0% | 0.0% | 0.0% | 0.0% |
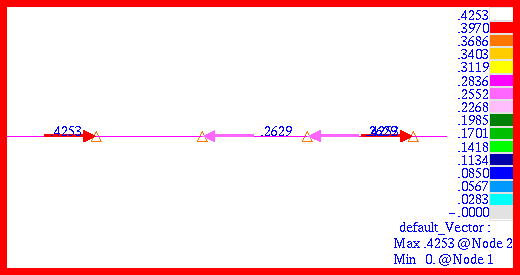
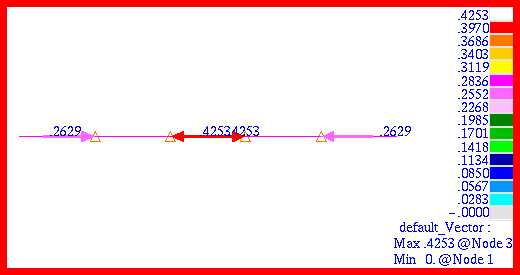
Due to the fact that all of the mode shapes merely involve horizontal displacements of the four masses, the mode shapes cannot be readily discerned by making combined fringe and deformation plots of the translational displacements associated with each eigenvector. Instead, vector plots were made of the translational displacement that were superimposed upon the deformed shape of the eigenvectors. In this way, the vectors would be drawn at the displaced position of each node, or mass. The eigenvectors and natural frequencies that were generated by Patran for the first modes are plotted in
Figure 14‑4 through
Figure 14‑7. Note that the natural frequencies recovered through Patran are identical to those obtained with MSC Nastran.
File(s): <install_dir>/results_vv_files/prob014.bdf, prob014.op2
Figure 14‑3 Spring and Mass Modal Model.
Figure 14‑4 Vector Plot of Mode 1.
Figure 14‑5 Vector Plot of Mode 2.
Figure 14‑6 Vector Plot of Mode 3.
Figure 14‑7 Vector Plot of Mode 4.
Problem 15: Normal Modes, Shells and Cylindrical Coordinates
Solution/Element Type:
MSC Nastran, Normal Modes, Solution 103, CTRIA3 Elements with Standard Formulation.
Reference:
Blevins, R.D., Formulas For Natural Frequency And Mode Shape, Kreiger Publishing Co., 1984, p. 240.
Problem Description:
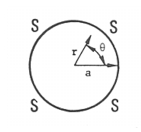
Find the natural frequencies and mode shapes for a simply supported flat circular plate.
Engineering Data:
a = radius = 4.0 inches | |
h = thickness = 0.25 inches |
E = elastic modulus = 107 psi |
|
|
Theoretical Solution:
For simply supported flat circular plate, the natural frequencies are given by the following expression:
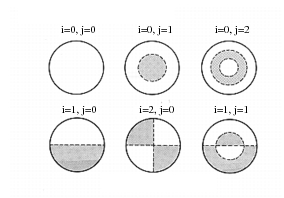
where for various values of i and j,
is given by:
Table 14‑3 
j | i |
0 | 1 | 2 |
0 | 4.977 | 13.94 | 25.65 |
1 | 29.76 | 48.51 | 70.14 |
2 | 74.20 | 102.8 | 134.3 |
3 | 138.3 | 176.8 | 218.2 |
The natural frequencies for various modes are listed and shown below.
MSC Nastran Results:
To compute the mode shapes for the plate, the model shown in
Figure 14‑8 was generated. Due to the cylindrical geometry, the model was meshed entirely with CTRIA3 elements which should provide accuracy better than a CQUAD4 element that is better suited for rectilinear geometry. In addition, the entire plate was modeled in order to provide better visualization of the modes. The following results were obtained.
Table 14‑4 i jSource | | | | | | |
Theory | 734.53 | 2057.33 | 3785.55 | 4392.13 | 7159.35 | 10950.81 |
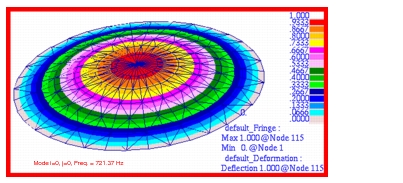
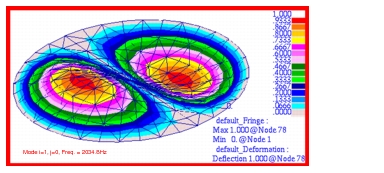
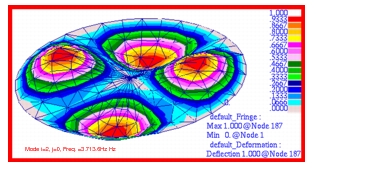
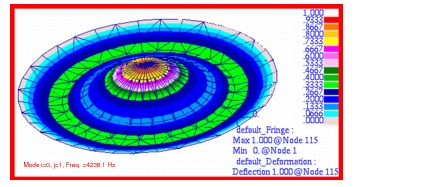
MSC Nastran | 721.37 | 2034.82 | 3713.55 | 4238.06 | 6941.60 | 10125.20 |
%, Difference | -1.79% | -1.09% | -1.90% | -3.51% | -3.04% | -7.54% |
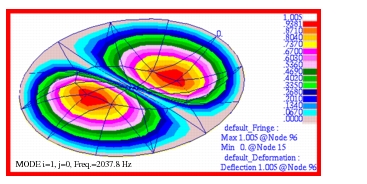
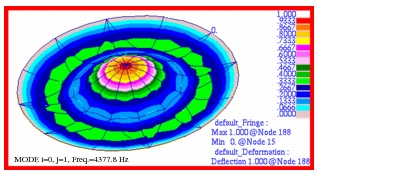
The corresponding combined fringe and deformation plots that were made for each of these modes are shown in
Figure 14‑10 through
Figure 14‑13 where the corresponding mode number and frequency have been clearly labeled.
File(s): <install_dir>/results_vv_files/prob015.bdf, prob015.op2
Figure 14‑8 Basic Circular Membrane Model with h-Elements.
Figure 14‑9 Mode 1, f00, for Membrane h-Element Model.
Figure 14‑10 Mode 2, f10, for Membrane h-Element Model.
Figure 14‑11 Mode 4, f20, for Membrane h-Element Model.
Figure 14‑12 Mode 6, f01, for Membrane h-Element Model.
Figure 14‑13 Mode 9, f11, for Membrane h-Element Model.
Figure 14‑14 Mode 15, f02, for Membrane h-Element Model.
Problem 16: Normal Modes, Pshells and Cylindrical Coordinates
Solution/Element Type:
MSC Nastran, Normal Modes, Solution 103, CTRIA, P-Formulation
Reference:
Blevins, R.D., Formulas For Natural Frequency and Mode Shape, Kreiger Publishing Co,. 1984, p. 240.
Problem Description:
This is a repeat of
Problem 15: Normal Modes, Shells and Cylindrical Coordinates, 7 which is to find the natural frequencies and mode shapes for a simply supported flat circular plate. In this instance, however, perform the calculation using cubic shell p-elements.
Theoretical Solution:
MSC Nastran Results:
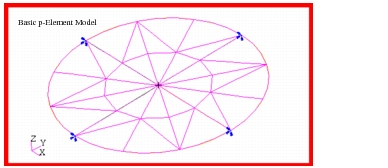
To compute the modes for the plate, the model shown in
Figure 14‑15 was generated using Patran. Due to the curvilinear geometry and nature of the modes shapes, the model was meshed entirely with triangular shell elements. In this instance, all of the elements were cubic TRIA13 p-elements. Due to the higher order of these elements, this permitted using a considerably sparser mesh than was used with simple linear TRIA3 elements in order to properly capture the various modes. A sparser mesh than what is shown in
Figure 14‑15 was found to only give reasonably accurate results for only the very lowest modes. The lack of an appropriate number of degrees of freedom necessarily precluded capturing some of the higher modes which typically exhibit considerably more complex shapes.
The following natural frequencies were calculated for some of the various modes.
Table 14‑5 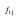
Source | | | | | | |
Theory | 734.53 | 2057.33 | 3785.55 | 4392.13 | 7159.35 | 10950.81 |
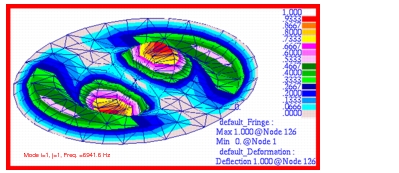
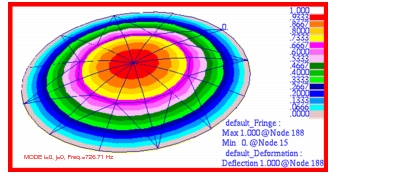
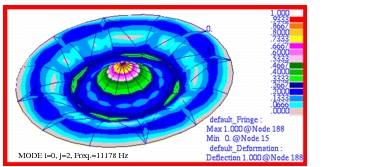
MSC Nastran | 726.71 | 2037.80 | 3736.80 | 4377.78 | 7259.80 | 11178.31 |
%, Difference | -1.06% | 0.95% | -1.29% | -0.33% | 1.40% | 2.08% |
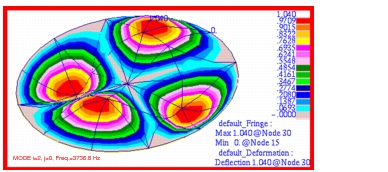
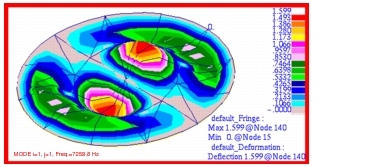
The corresponding combined fringe and deformation plots that were made with Patran for each of these modes are shown in
Figure 14‑16 through
Figure 14‑20 where the mode number and frequency have been clearly labeled. A comparison of these figures with the figures of
Problem 15: Normal Modes, Shells and Cylindrical Coordinates, 7 clearly shows that the predicted mode shapes are being accurately predicted by MSC Nastran and displayed with Patran. In addition, it is interesting to note that the use of higher order pshell elements gives comparable accuracy for the first couple of primary modes but gives noticeably more accurate results for the higher order modes, the error being typically about one-fourth or less.
File(s): <install_dir>/results_vv_files/prob016.bdf, prob016.op2
Figure 14‑15 Basic p-Element Membrane Model.
Figure 14‑16 Mode 1, f00, of p-Element Membrane Model.
Figure 14‑17 Mode 2, f10, of p-Element Membrane Model.
Figure 14‑18 Mode 4, f20, of p-Element Membrane Model.
Figure 14‑19 Mode 6, f01, of p-Element Membrane Model.
Figure 14‑20 Mode 9, f11, for Membrane p-Element Model.
Figure 14‑21 Mode 15, f02, of p-Element Membrane Model.
Problem 17: Buckling, shells and Cylindrical Coordinates
Solution/Element Type:
MSC Nastran, Buckling, Solution 105, CTRIA3, CQUAD4 Elements with Standard Formulation.
Reference:
Roark, R.J., and Young, W.C., Formulas For Stress and Strain, 5th ed., McGraw-Hill, Book Company, 1975, p. 556.
Problem Description:
Find the critical buckling pressure for a thin wailed cylinder with closed ends subjected to a uniform external pressure both laterally and longitudinally. Assume the endcaps and cylinder have the same thickness and that the ends are held circular.
Engineering Data:
Theoretical Solution:
For a thin walled cylinder with closed ends subjected to a uniform external pressure both axially and longitudinally, the critical buckling pressure is given by the following expression:
where

equals the number of lobes formed by the tube when it buckles.
Upon substitution of the engineering design parameters into the preceding equation, it can be shown that the minimum buckling pressure corresponds to a three lobed buckling mode shape. This occurs at a critical pressure equal to:
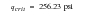
.
MSC Nastran Results:
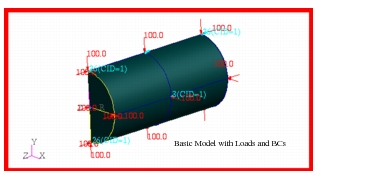
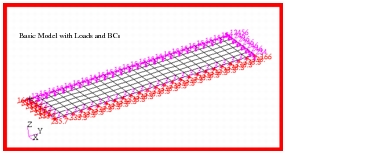
To compute the critical buckling pressure for the cylinder, the model shown in
Figure 14‑22 was generated using Patran. The lateral sides of the cylinder were meshed with CQUAD4 elements while owing to the curvilinear geometry, the endcaps were meshed with CTRIA3 elements to maximize accuracy. Due to symmetry, only half of the cylinder was modeled with the appropriate symmetry boundary conditions being applied along the free edges. Additional symmetry boundary conditions were applied along the midplane of the cylinder. Also, to prevent recovery of any modes associated with buckling of just the endcaps, the center of each cap was restrained against any motion in either the radial, tangential or axial directions.
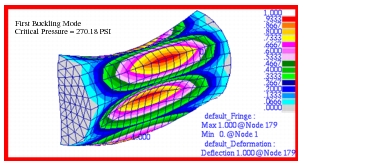
A buckling calculation was performed using MSC Nastran. The critical buckling pressure was predicted to be:
Table 14‑6 Theory | 256.23psi |
MSC Nastran | 270.18psi |
%, Difference | 5.44% |
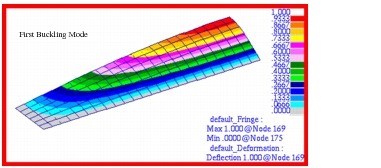
The corresponding mode shape was plotted with Patran and is shown in
Figure 14‑23. The mode shape clearly shows two distinct lobes present on the half of the cylinder that was modeled, with an additional lobe present on the other half that was not included due to symmetry.
File(s): <install_dir>/results_vv_files/prob017.bdf, prob017.op2
Figure 14‑22 Cylinder Buckling Model with Loads and BCs.
Figure 14‑23 Three Lobed Mode Corresponding to Critical Pressure.
Problem 18: Buckling, Flat Plates
Solution/Element Type:
MSC Nastran, Buckling, Solution 105, CQUAD4 with Standard Formulation.
Reference:
Roark, R. J., and Young, W. C., Formulas For Stress and Strain, 5th ed., McGraw-Hill Book Company, 1975, p. 551.
Problem Description:
A simply supported flat rectangular plate is subjected to a uniform compressive edge load. Find the critical buckling edge load and corresponding buckling mode shape.
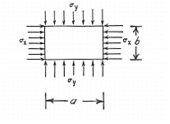
Engineering Data:
Theoretical Solution:
For a simply supported plate subjected to edge pressures
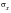
and
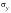
, the critical edge pressure required to induce buckling is given by:
Here m and n signify the number of half-waves in the buckled plate in the x and y directions respectively. Assuming that:
and:
yields:
Substitution of the design parameters for the plate yields a critical edge pressure of:
which corresponds to a distributed edge load of 613.313 lbs / inch.
MSC Nastran Results:
To compute the critical buckling load and mode shape for the plate, the model shown in
Figure 14‑24 was created using Patran. Due to symmetry, only one-fourth of the plate was modeled with the appropriate boundary conditions being applied along the planes of symmetry. In addition to further enforce recovery of only the lowest mode, additional boundary conditions were imposed so that there were no surface rotations about axes located in either plane of symmetry. This would ensure that only symmetrical mode shapes were calculated. Lastly, compressive edge pressures were modeled as distributed edge loads equal to the edge pressure multiplied by the plate thickness. Using this model, MSC Nastran calculated the critical edge pressure to be:
Table 14‑7 Theory | |
MSC Nastran | |
%, Difference | 0.002% |
The corresponding buckling mode shape that was plotted using Patran is shown in
Figure 14‑25. The mode shape plot clearly reveals the presence of a half-sine wave in either the x or y directions, which would correspond to
m =
n = 1.
File(s): <install_dir>/results_vv_files/prob018.bdf, prob018.op2
Figure 14‑24 Plate Buckling Model with Load and BCs.
Figure 14‑25 Buckling Mode Shape of Plate due to Critical Pressure.
Problem 19: Direct Transient Response, Solids and Cylindrical Coordinates
Solution Type:
Direct Linear Transient Response, Solution 109
Element Type:
CHEX8, Standard Formulation
Reference:
Crandall, S. H., Dahl, N.C., and Lardner, T.J., An Introduction to the Mechanics of Solids, 2nd ed., Mc-Graw Hill Book Company, 1972, pp. 293-297.
Problem Description:
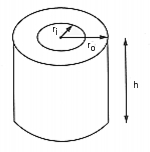
A thick walled cylinder is subjected to a sudden internal pressure of 10 psi. Find the peak radial displacement in the cylinder due to the sudden application of the pressure.
Engineering Data:
ri = 6.0 inches | |
r0 = 12.0 inches |
h = 8.0 inches |
E = 30.0 x 106 psi |
|
|
P = 10.0 psi |
Theoretical Results:
For a single degree-of-freedom system, an instantaneously applied load will give a maximum displacement that is twice the static displacement at the same applied loading.
MSC Nastran Results:
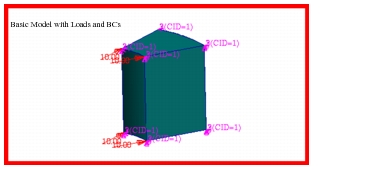
To determine the transient response of the cylinder, the model shown in
Figure 14‑26 was generated using Patran. Due to symmetry, only a 15 degree sector of the cylinder was modeled with the appropriate axisymmetric boundary conditions applied to the lateral faces of the model. The model was meshed entirely with CHEX8 solid elements using a standard formulation.
For the purposes of this analysis, the pressure was applied in an instantaneous manner as shown below. Several time steps of zero load were input to ensure simulation of a sudden step function in the loading. The integration time step was chosen to be 1.0 microsecond. To prevent numerical instability, the applied loading was ramped over a single time step. Approximately three cycles of the response were simulated and structural damping was neglected with the radial displacement being recovered at three radial positions situated at the inner diameter, midway through and at the outer diameter of the cylinder.
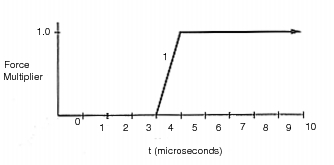
Using the same model, a static analysis was performed with a constant internal pressure of 10.0 psi. The results for both the static and transient analysis are summarized below.
Table 14‑8 Position | Static Displacement 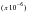 | Peak Transient Displacement | Ratio Transient/Static |
| 3.325737 | 6.534348 | 1.965 |
| 2.773202 | 5.534836 | 1.996 |
| 2.662867 | 5.322965 | 1.999 |
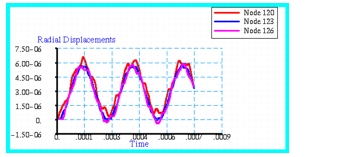
An XY Plot that was generated by Patran of the transient radial displacement at inner, mean, and outer radius is shown in
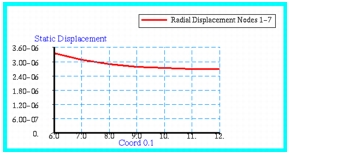
Figure 14‑28. In this figure nodes 120, 123 and 126 correspond to the inner, mean and outer radius, respectively. The results clearly show the expected oscillatory behavior characteristic of an undamped response. The corresponding static results are shown in
Figure 14‑29 where the radial displacement has been plotted against radius.
A fringe plot of the static radial displacements is shown in
Figure 14‑27. Both the fringe and xyplots clearly show peak values that agree with he preceding MSC Nastran results.
File(s): <install_dir>/results_vv_files/prob019_T.bdf, prob019_T.op2, prob019_S.bdf, prob019_S.op2
Figure 14‑26 Transient Dynamic Model of Cylinder.
Figure 14‑27 Corresponding Static Results of Displacement.
Figure 14‑28 Displacement Responses at Various Nodes.
Figure 14‑29 Corresponding Static Displacements Across Thickness.
Problem 20:Modal Transient Response with Guyan Reduction and Bars, Springs, Concentrated Masses and Rigid Body Elements
Solution/Element Type:
MSC Nastran, Modal Transient Response, Solution 112, CBAR, CONM2, CMASS1, CELAS1, RBE2.
Reference:
MSC.Nastran Demonstration Problem Manual, Version 65
Problem Description:
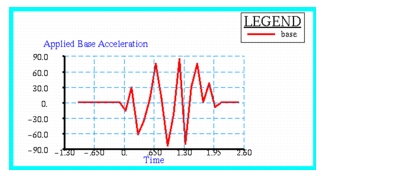
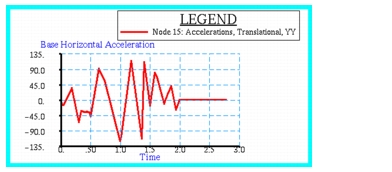
The transient response is required of a two dimensional truss mounted on an elastic foundation and subjected to a time dependent base excitation. The truss is shown below and consists of bars of varying cross-section with localized concentrated masses. The horizontal acceleration that is applied to the base is shown plotted in
Figure 14‑30.
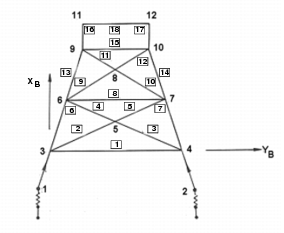
Engineering Data:
Table 14‑9 Bar ID | Area | I1 |
1 | 36.91371 | 2549.353 |
2 through 5 | 30.63052 | 1456.865 |
6,7,13,14 | 266.83900 | 47701.650 |
8 | 30.63052 | 1456.865 |
6 through 12 | 24.34734 | 731.942 |
15, 18 | 147.65490 | 40789.650 |
16, 17 | 162.57740 | 24234.200 |
19, 20 | 537.21123 | 22965.830 |
Table 14‑10 Direction | Stiffness |
Vertically | 23.0 x 10 5 |
Horizontally | 1.0 x 10 5 |
Rotationally | 15.0 x 10 9 |
Table 14‑11 Location (Point ID) | Mass |
15, Horizontal | 8.0 x 10 9 |
15, Vertical | 8.0 x 10 9 |
15, Rotational | 4.0 x 10 15 |
3, 4, 6, 7 | 388.1988 |
5, 8 | 25.8799 |
9, 10 | 1035.197 |
11, 12 | 2070.393 |
Theoretical Solution:
For this particular problem there exists no simple closed form solution. The only real means of ascertaining the accuracy of a MSC Nastran analysis model is to ensure that the base acceleration matches the intended profile of the applied excitation. This is a basic check that should always be performed, especially when using the large mass method to simulate an enforced base motion.
MSC Nastran Results:
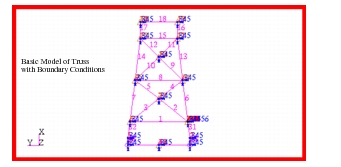
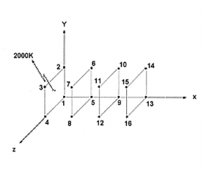
To calculate the transient response for the truss, the model shown in
Figure 14‑31 was generated using Patran. The model was comprised of simple CBAR elements and CONM2 elements that were used to model any localized masses, with the exception of the base point (i.e., Node 15). To model the base, three large grounded scalar mass CMASS1 elements were used, one each for the horizontal, vertical and rotational directions. The magnitude of these masses were chosen to be approximately 10
9 times as great as the mass of the truss. By doing so, this would ensure that the large mass of the base would dominate so that the intended base excitation was properly applied to the entire truss. A single RBE2 rigid body element was used to attach the base node to the ends of the CELAS1 elements that were used to model the elastic foundation.
In performing the analysis, the modal transient method was used along with automated Guyan reduction. The transient response was based upon the first 30 modes which spanned a frequency range that extended to approximately 100 hertz. This was deemed more than acceptable, given the periodicity of the applied base acceleration profile. In addition, it was assumed that throughout this entire frequency range, the truss was 10 percent critically damped.
The resultant acceleration profile that was predicted by MSC Nastran at the base point is shown plotted in
Figure 14‑32. Here the horizontal acceleration at node 15 has been plotted versus time using the results xyplot utility of Patran. It can clearly be seen that the acceleration at Node 15 closely matches the intended base excitation which was previously shown in
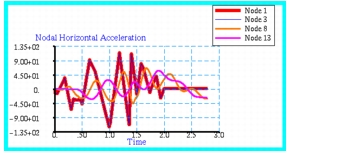
Figure 14‑30. The acceleration at other selected nodes on the model are shown plotted in
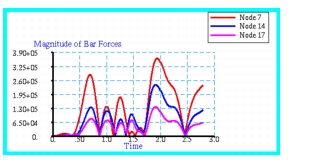
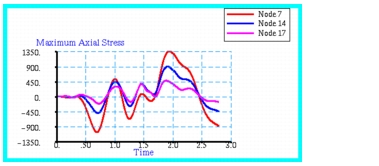
Figure 14‑33. These acceleration profiles appear to show the correct response. Namely, the occurrence of any localized peaks in the base acceleration are matched by localized peaks in the acceleration of the truss. Similarly, the magnitude of the bar forces and stress response plots, shown in
Figure 14‑34 and
Figure 14‑35, exhibit the same behavior.
File(s): <install_dir>/results_vv_files/prob020.bdf, prob020.op2
Figure 14‑30 Horizontal Acceleration Applied to Truss.
Figure 14‑31 Basic Model of 2D-Truss Structure.
Figure 14‑32 Horizontal Acceleration Profile at Base (Node 15).
Figure 14‑33 Horizontal Acceleration at Selected Points of 2D-Truss.
Figure 14‑34 Bar Force Responses at Selected Points in 2D-Truss.
Figure 14‑35 Stress Responses at Selected Points in 2D-Truss.
Problem 21: Direct Nonlinear Transient, Stress Wave Propagation with 1D Elements
Solution/Element Type:
MSC Nastran, Direct Nonlinear Transient, Solution 129, CROD Elements
Reference:
Timoshenko, S., and Goodier, J. N., Theory of Elasticity, 2nd ed., McGraw-Hill Book Co., 1951, pp. 492-496.
Juvinall, R.C., Engineering Consideration of Stress, Strain and Strength, McGraw-Hill Book Co., 1967, pp. 185-188.
Problem Description:
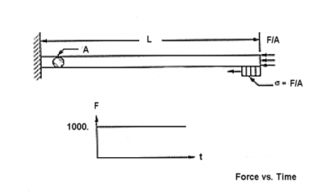
A rod of uniform cross section is fixed at one end and a constant force is suddenly applied to its free end. A stress wave results that propagates along the length of the rod. Determine the stress history at both the free and fixed ends of the rod as well as the displacement history at the free end.
Engineering Data:
L = rod length = 100.0 m | A = cross-sectional area of the rod = 1.0 m2 |
E = elastic modulus = 103 N/m2 | |
| |
Theoretical Solution:
Due to the constant force, F, applied at the free end of the rod, the stress at the free end remains constant and is simply equal to
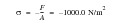
+
Before the stress wave first reaches the fixed end, the stress at the fixed end is zero. As soon as the stress wave arrives at the fixed end, it is reflected and produces a stress equal to
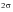
at the fixed end. The stress remains unchanged until the wave front returns to this point. The compressive wave leaves the fixed end and upon reaching the free end it is once again reflected, but this time as a tensile wave. When this tensile wave arrives at the fixed end and is reflected, the stress at the fixed end becomes zero. This zero stress state will again remain unchanged for another complete cycle of the stress wave motion.
The displacement time history at the free end can be expressed as
Or, expressing u(t) separately for each time interval
,
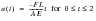
etc.
Thus, the displacement at the free end is a linear function of time during each interval it takes the stress wave to completely traverse the rod.
MSC Nastran Results:
To determine the stress and displacement history at the opposing ends of the rod, the model shown in
Figure 14‑36 was generated using Patran. The model consisted of 20 CROD elements. One end was fixed while the remainder of the rod was constrained to motion in the x, or axial, direction only. The upper bound stability limit for the integration time increment was determined by:
where
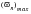
is the highest natural frequency in cycles per second of all of the modes of interest in the model. In this instance, this would mandate that modal frequencies be at least greater than the frequency associated with one complete cycle for the stress wave to completely traverse the rod, or 0.5 cycles per second. For the purposes of this analysis, an integration time increment of 0.025 seconds was used. In addition, a slight amount of damping was introduced to reduce the overall occurrence of any oscillations in the solution.
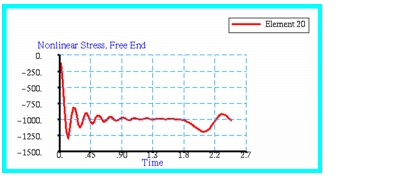
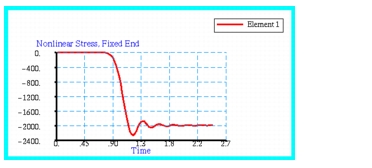
Stress history plots that were made with Patran of the MSC Nastran results are shown in
Figure 14‑37 and
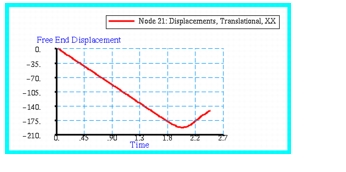
Figure 14‑38 for the fixed and free ends of the rod, respectively. The displacement history at the free end of the rod is shown plotted in
Figure 14‑39. Despite the presence of the damping, the results do exhibit some slight oscillations, especially whenever a stress wave is reflected as well as upon initial application of the loading. However, these oscillations are rapidly attenuated. Overall, the results demonstrate the correct periodicity of the stress and displacement at both the fixed and free ends of the rod.
Table 14‑12 Theory | 200.00 m |
MSC Nastran | 200.98 m |
%, Difference | 0.49% |
Table 14‑13 Theory | |
MSC Nastran | |
%, Difference | 13.23% |
File(s): <install_dir>/results_vv_files/prob021.bdf, prob021.op2
Figure 14‑36 Basic CROD Model to Investigate Stress Wave.
Figure 14‑37 Stress History Plot at Element 20, the Free End.
Figure 14‑38 Stress History Plot at Element 1, the Fixed End.
Figure 14‑39 Free End Displacement of CROD Model.
Problem 22: Direct Nonlinear Transient, Impact with 1D, Concentrated Mass and Gap Elements
Solution/Element Type:
MSC Nastran, Direct Nonlinear Transient, Solution 129, CROD, CGAP, CONM2 Elements.
Reference:
Timoshenko, S., and Goodier, J.N., Theory of Elasticity, 2nd ed., McGraw-Hill Book Co., 1951, pp. 497-504
April 1986 Application Note, Application Manual Section 5.
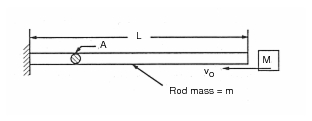
Problem Description:
A rod with a fixed end is struck by a moving mass at its other end. Let 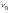 be the initial velocity of the mass prior to impact. Consider the mass of the body to be infinitely rigid and the velocity at the free end of the rod at the instant of impact to also be equal to
be the initial velocity of the mass prior to impact. Consider the mass of the body to be infinitely rigid and the velocity at the free end of the rod at the instant of impact to also be equal to 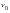 . Determine the time history of stress and displacement at the free end of the rod as well as the duration of the impact and the maximum stress in the rod.
. Determine the time history of stress and displacement at the free end of the rod as well as the duration of the impact and the maximum stress in the rod. Engineering Data:
Theoretical Solution
At the instant of impact, an initial compressive stress is generated at the free end of the rod equal to:
or upon substitution:
After impact, the resistance of the bar will cause the velocity of the moving body to decrease and hence the pressure on the bar will decrease as well, causing a reduction in the compressive stress in the bar. Thus, there exists a compressive wave characterized by a decreasing compressive stress traveling along the length of the bar. The change in compressive stress with time can easily be determined from the equation of motion of the body. Letting
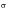
denote the variable compressive stress at the free end of the bar and v the variable velocity of the body yields:
or upon substituting
yields:
from which
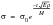
This equation is only valid so long as
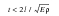
, or
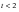
seconds. At t = 2 seconds, the compressive wave with an intensity of
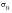
returns to the free end of the bar, which is still in contact with the body. The velocity of the body cannot change suddenly. As a consequence, the stress wave will be reflected from the end of the bar, resulting in an immediate increase in the compressive stress to
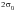
. This sudden change in compressive stress occurs during impact at the end of every two second interval. However, during every subsequent interval, there will be an increasing number of stress waves either moving away or toward the struck end of the rod. The compressive stress at the free end of the rod at any instant will simply be the sum of the stress induced by the reflected waves produced during that particular interval with the stress produced by the returning waves from the previous interval. The actual peak stress produced in the rod throughout impact will occur in a different interval depending upon the ratio
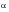
of the mass of the rod to the mass of the body. For the case

, the max stress occurs at t = 2 seconds and is equal to
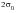
.
The instant when the stress at the free end of the rod becomes zero indicates the end of impact. In general the duration of the impact increases as
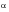
decreases. Calculations of Saint-Venant give the following values for impact duration:
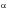 = | 1/6 | 1/4 | 1/2 | 1 |
Duration | 7.419 | 5.900 | 4.708 | 3.068 |
MSC Nastran Results:
To determine stress and displacement history at the free end of the rod, the model shown in Figure 14‑40 was generated using Patran
. The model consisted of 20 CROD elements. The end of one CROD element was completely restrained while the remainder were constrained to motion in the x, or axial, direction only. The mass was modeled with a CONM2 concentrated mass element which was connected to the free end of the rod with a gap element having a zero initial opening. An initial velocity of
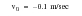
was specified for both the CONM2 and the node situated at the free end of the rod. An integration time step of 0.025 seconds was chosen and a small damping of 0.4% was introduced to red
uce any high frequency oscillations in the solution. The MSC Nastran results are shown in
Figure 14‑41 and
Figure 14‑42. Here, the stress history and displacement history at the free end of the rod were plotted using Patran. Also shown in
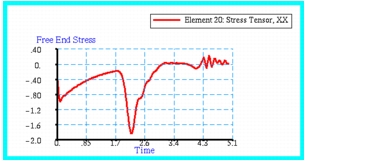
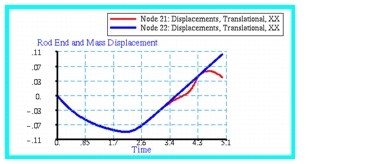
Figure 14‑42 is the displacement history of the mass, designated as Node 22. The results show the expected behavior; namely, an initial compressive stress of

that rapidly decays until 2 seconds at which time it immediately doubles and then decays to a value of zero. The time at which the stress reaches zero also correlates in
Figure 14‑42 with the mass and rod tip no longer moving in unison, which signifies the end of impact.
Table 14‑14 Source | Max Stress 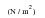 | Impact Duration (sec) |
Theory | -2.00 | 3.068 |
MSC Nastran | -1.84 | 3.075 |
%, Difference | -8.0% | 0.23% |
File(s): <install_dir>/results_vv_files/prob022.bdf, prob022.op2
Figure 14‑40 Basic Model of Impact Analysis.
Figure 14‑41 Free End Stress Response of Impact Model.
Figure 14‑42 Rod End and Mass Displacement Responses.
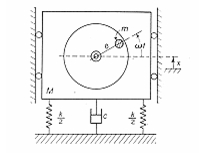
Problem 23: Direct Frequency Response, Eccentric Rotating Mass with Variable Damping
Solution/Element Type:
MSC Nastran, Direct Frequency Response, Solution 108, CBAR, CELAS1, CDAMP1, and CONM2 Elements.
Reference:
Thomson, W. T., Theory of Vibration with Applications, Prentice-Hall, Inc., 1972, pp. 45-52.
Problem Description:
A spring mass system is constrained to move in the vertical direction and is excited by a rotating machine that is unbalanced as shown below. The unbalance is represented by an eccentric mass, m, with eccentricity, e, which is rotating at an angular velocity, 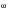 . Determine the undamped resonant frequency as well as the amplitude at this frequency when the damping is varied.
. Determine the undamped resonant frequency as well as the amplitude at this frequency when the damping is varied. Engineering Data:
k = spring constant = 1000.0 lbf / inch | |
c = 2.5, 10.0 or 30.0 lbf-sec / inch |
e = 0.1 inch |
|
|
The resonant amplitude is then given by
For c = 2.5, | | |
For c = 10.0, | | |
For c = 30.0, | | |
MSC Nastran Results:
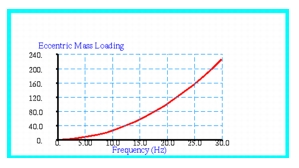
To model the eccentrically rotating mass system, the model shown in Figure 14‑43 was generated using Patran
. To improve visualization, the nonrotating mass was modeled as a rod using two CBAR elements. The rod had a total mass equal to that of the nonrotating mass (M - m) and the eccentric mass m, or 0.25 lb-sec2/inch. The ends of the rod were constrained to move in the y, or vertical, direction only. The ends of the rod were attached to grounded springs, each with a stiffness of 500 lbs/inch. The center of the rod was attached to a grounded damper. In addition, at the center of the rod, the force due to the rotation of the eccentric mass was applied. A plot of the applied force versus frequency is shown in Figure 14‑44. Using this model, a frequency response analysis was performed whereby the frequency and rotational loading was varied over a range of 0 to 30 hertz. The displacement at the center of the rod was recovered and is shown plotted in
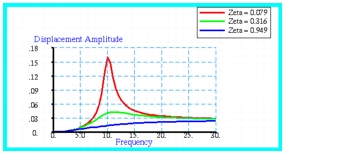
Figure 14‑45. Here the MSC Nastran results have been plotted with the aid of Patran for each of the damping ratios that were examined. The magnitude of the complex results is plotted. The results clearly reveal the presence of a resonant spike occurring at about 10 hertz that becomes rapidly attenuated as the damping is increased. At the highest damping level, a critically damped response is highly evident that is characterized by the absence of any amplification in the displacement at the resonant frequency.
Table 14‑15 Source | | | |
Theory | 0.160236 | 0.0400509 | 0.0133503 |
MSC Nastran | 0.1586090 | 0.0397802 | 0.0132626 |
%, Difference | -0.995% | -0.676% | -0.657% |
File(s): <install_dir>/results_vv_files/prob023_1.bdf, prob023_1.op2, prob023_2.bdf, prob023_2.op2, prob023_3.bdf, prob023_3.op2
Figure 14‑43 Basic Model of Direct Frequency Response Analysis.
Figure 14‑44 Applied Force versus Frequency.
Figure 14‑45 Amplitude Displacements at Center of Rod.
Problem 24: Modal Frequency Response, Enforced Base Motion with Modal Damping and Rigid Body Elements
Solution/Element Type:
MSC NastranModal Frequency Response, Solution 111, CQUAD4, CELAS1, CONM2, and RBE2 Elements.
Reference:
Thomson, W.T., Theory of Vibration with Applications, Prentice-Hall, Inc., 1972, pp. 45-49.
Problem Description:
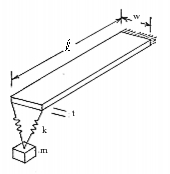
A long thin cantilevered plate has a concentrated mass suspended from its free end by two parallel springs. The base of the plate is excited by a sinusoidal excitation producing a peak unit acceleration. Find the resultant acceleration response of the suspended mass and the tip of the plate over a frequency range of zero to 100 hertz.
Engineering Data:
l = 12.0 inches | |
w = 2.0 inches |
t = 0.5 inches |
k = 50 lbf / inch |
|
|
|
|
|
Theoretical Solution:
For the cantilevered plate and suspended mass, the application of a sinusoidal base excitation will produce a resonant spike at each of the mode shapes associated with the end mass and with the tip of the plate. The amplitude induced at resonance will be a function of the amount of damping present. To determine where the expected resonant points occur, it is first necessary to estimate the natural frequencies for the end mass and plate.
First consider the end mass. This mass is suspended by two parallel springs whose total combined stiffness is simply the sum of the two. However, this combined spring is in series with another spring determined by the stiffness of the plate. For a cantilevered plate, the spring stiffness is given by:
Substituting the assumed engineering data gives:
The total effective combined stiffness of the plate and the end springs is given by
The resonant frequency for the end mass then becomes:
For the cantilevered plate, the resonant frequencies are given by
where  is the mass per unit length.
is the mass per unit length. For the first two modes:
This gives for the plate:
Since there exists a single resonant frequency associated with the motion of the end mass that lies within the frequency range of interest, the application of a unit base acceleration should cause a resonant response only at frequencies in the vicinity of 1.933 hertz. In contrast, for a point situated on the end of the plate, two additional resonant spikes will occur at frequencies near 10.99 hertz and 68.89 hertz.
For a harmonically excited damped oscillator, the width of the resonant spike is expressed by the factor Q which is defined as:
where
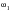
and
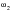
refer to those frequencies above and below
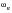
where the response is approximately 70 percent of the response that occurs when

. These frequencies are referred to as the half power points. If the damping remains fixed over the entire frequency range of interest, then the bandwidth about the resonant points must be noticeably greater at the higher natural frequencies. Thus, a very narrow band response should be observed at low frequencies becoming increasingly broadband at the natural frequencies associated with the higher modes.
MSC Nastran Results
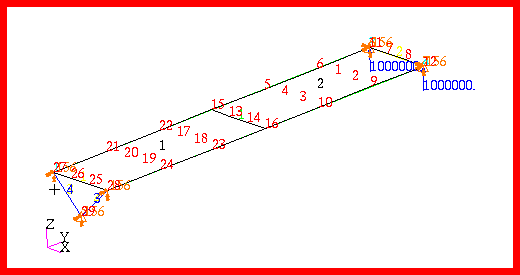
To determine the frequency response of the system, the model shown in
Figure 14‑46 was generated using Patran. The plate was modeled using standard CQUAD4 elements. The end mass was modeled using a lumped mass CONM2 element which was attached to the plate with two CELAS1 linear spring elements. To simulate the base, the other end of the plate was attached to an RBE2 rigid body element. At the independent node for the RBE2 element, a large concentrated mass was placed and excited by a force of sufficient magnitude to cause a unit acceleration throughout the frequency range of interest. The magnitude of the mass for the base was chosen to be 10
6 times as great as the entire mass of the plate and suspended end mass. This would ensure that the inertia of the base would dominate and impose the desired enforced motion. For the purpose of this analysis, the model was purposely constrained to prevent any lateral motion.
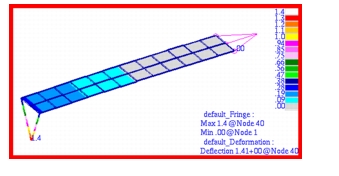
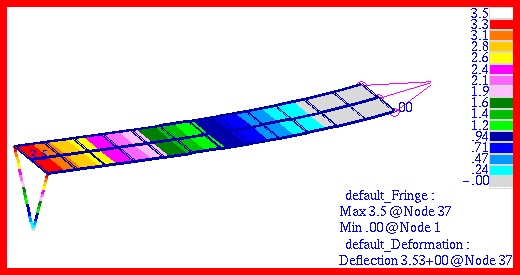
Before determining the frequency response of the plate-mass system, a modal analysis was performed to determine the natural frequencies and corresponding mode shapes. The first three predicted modes were plotted using Patran and are shown in
Figure 14‑47 through
Figure 14‑49. Also displayed in these figures are the corresponding natural frequencies. Examination of these figures shows excellent agreement with the predicted modes. The first mode is predominately associated with motion of the end mass, whereas the higher modes mainly entail excitation of the plate. On the basis of the modal analysis, a frequency response analysis should exhibit a resonant peak in the acceleration occurring 2.0054, 12.84 and 71.134 hertz.
A subsequent frequency response analysis was performed with the preceding model using the modal method. For the purpose of this analysis, only the first five modes were retained, which included frequencies up to 195 hertz. This was deemed satisfactory since the maximum frequency of interest was only 100 hertz. The accelerations were recovered at the base, the suspended end mass and at the tip of the plate. These accelerations are shown plotted in
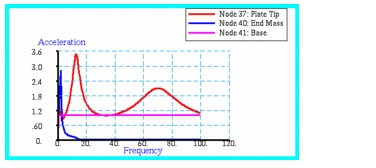
Figure 14‑50 where the magnitude of the complex result has been plotted. The resultant accelerations show the correct behavior. The end mass shows a single resonant spike at the first mode, or approximately 2 hertz, whereas the plate tip shows three distinct resonance points occurring at each of the three natural frequencies that were previously calculated. In addition, the base shows a uniform unit acceleration over the entire frequency band, clearly indicating that a sufficiently large mass was chosen to obtain the desired enforced motion. Lastly, the resonant spikes for the plate tip shows an increasingly broadband behavior that would be consistent with a constant Q, or damped system.
For the problem at hand, there exists no rigorous closed form solution. The presence of the elastically suspended mass on a cantilevered plate creates a multi degree of freedom system. Closed form solutions only exist for single degree of freedom damped oscillators. Nevertheless, the estimated modes show the correct mode shapes and are occurring at approximately the expected natural frequencies. In addition, resonant peaks are occurring in the vicinity of the predicted natural frequencies, with an increasing broadband response at the higher modes that would be indicative of uniform modal damping.
File(s): <install_dir>/results_vv_files/prob024_1.bdf, prob024_1.op2, prob024_2.bdf, prob024_2.op2
Figure 14‑46 Model of Beam with Suspended Mass.
Figure 14‑47 First Mode Shape of Beam, Freq=2.0054 Hz.
Figure 14‑48 Second Mode Shape of Beam, Freq = 12.84 Hz.
Figure 14‑49 Third Mode Shape of Beam, Freq = 71.134 Hz.
Figure 14‑50 Acceleration Responses of Plate Tip, End Mass, and Base.
Problem 25:Modal Frequency Response, Enforced Base Motion with Modal Damping and Shell P-Elements
Solution/Element Type:
MSC Nastran, Modal Frequency Response, Solution 111, CQUAD16, CELAS1, CONM2
Reference:
Thomson, W.T., Theory of Vibration with Applications, Prentice-Hall, Inc., 1972, pp. 41, 108, 158.
Problem Description
This is a repeat of Problem 24: Modal Frequency Response, Enforced Base Motion with Modal Damping and Rigid Body Elements, 46 with the exception that cubic QUAD16 pshell elements were used to model the plate. See this problem for a description of the model and all relevant engineering data. Theoretical Solution
MSC Nastran Results:
To determine the frequency response of the suspended end mass and the tip of the plate, the model shown in
Figure 14‑51 was generated using Patran. In this instance, the plate was modeled using two cubic QUAD16 elements. The suspended mass was attached to the end of the plate using CELAS1 elements. Since RBE2 elements are not functional with p-elements, this necessitated that two large masses be attached directly to the corners at the base of the plate. At the site of the large masses, two sinusoidal forces were applied that were of sufficient magnitude to impart a unit acceleration throughout the entire frequency range of interest, or zero to 100 hertz. As before, base masses were chosen that were on the order of 106 times the mass of the plate and the suspended end mass. This would ensure that the desired enforced motion was being imparted at the base of the plate. In addition, a constant 10% critical modal damping was assumed.
Using the preceding model, a modal analysis was performed to determine all of the relevant modes that existed in the frequency range between zero and 100 hertz. The results of this analysis showed the existence of three distinct modes at the following frequencies:
Table 14‑16 Mode Number | Natural Frequency (Hertz) |
1 | 2.009 |
2 | 12.984 |
3 | 72.613 |
The corresponding mode shapes were identical to those shown in
Figure 14‑47 through
Figure 14‑49 of
Problem 24: Modal Frequency Response, Enforced Base Motion with Modal Damping and Rigid Body Elements, 46. In addition, the predicted natural frequencies closely matched those that were obtained with linear CQUAD4 elements, which were 2.0054, 12.840 and 71.134 hertz. The results of a frequency response analysis are shown in
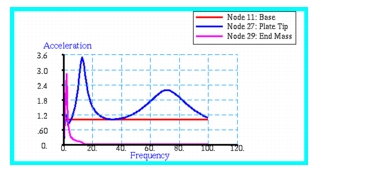
Figure 14‑52. Here the predicted accelerations at the base and tip of the plate and as well as at the suspended mass have been plotted versus frequency. The results show the correct response. Namely, resonant spikes are clearly evident at each of the predicted natural frequencies. The acceleration plot for the end mass shows a single resonance point since only one modes exit below 100 hertz. In contrast, the acceleration plot for the plate tip shows three distinct resonance peaks that correspond to the three predicted modes. A constant unit acceleration is predicted at the base of the plate, indicating that a large enough mass was used when modeling the base in order to impart the desired enforced motion. A comparison of the acceleration profiles plotted in
Figure 14‑47 with those shown in
Figure 14‑50 of Problem 24, clearly indicate that nearly identical results were obtained when using either QUAD4 elements with a standard h-shell formulation or QUAD16 cubic elements with a p-formulation. The actual peak accelerations that were obtained with both element types are summarized below.
Table 14‑17 Element Type | Peak Acceleration, Mode 1 |
QUAD4 | 2.798 |
QUAD16 | 2.795 |
%, Difference | -0.107% |
Table 14‑18 Element Type | Mode 1 | Mode 2 | Mode 3 |
QUAD4 | 1.170 | 3.448 | 2.084 |
QUAD16 | 1.170 | 3.480 | 2.168 |
%, Difference | 0.0% | 0.928% | 4.03% |
File(s): <install_dir>/results_vv_files/prob025.bdf, prob025.op2
Figure 14‑51 p-Element Model of Plate with Suspended Mass.
Figure 14‑52 Acceleration Responses of Plate Tip, End Mass, and Base.
Problem 26: Complex Modes, Direct Method
Solution/Element Type:
MSC Nastran, Complex Modes, Solution 107, CBAR, CONM2, CELAS1, and CDAMP Elements.
Reference:
Thompson, W.T., Theory of Vibration With Applications, Prentice-Hall,1972, pp. 23-27.
Blevins, R.D., Formulas For Natural Frequency And Mode Shape, Kreiger Publishing Co., 1979, p. 77.
Problem Description:
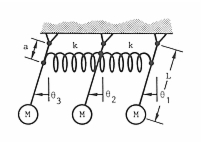
Three equal masses are each supported by a massless pendulum. Each pendulum is in turn coupled to the other two pendulums by a linear spring. In addition, there is a rotational damper located at the pivot point for each pendulum. Assuming that each damper has a different strength, determine the complex modes and natural frequencies for this coupled spring-mass system.
Engineering Data:
L = 5 inches | |
a = 5 inches |
k = 500 lbf / inch |
M = 0.01 lbf - sec 2 / inch |
C1 = 120 lbf - sec |
C2 = 60 lbf - sec |
C3 = 20 lbf - sec |
Theoretical Solution:
For the undamped case, there are three modes associated with the angular displacements for each pendulum. The relative angular displacement for each mode are as follows:
The corresponding natural frequencies associated with each mode are
where g refers to gravitational constant, or 386.4 inches/sec2. Substituting in the assumed engineering values yields the following undamped natural frequencies:
When damping is present, the damped natural frequency is given by the expression:
where
and ccrit is the critical damping required to just suppress any oscillatory motion. For a simple pendulous mass, ccrit can be expressed as:
To estimate the natural frequencies for the three damped oscillators, the average critical damping ratio is computed.
For the first mode, all of the masses are moving in unison. Thus, the most highly damped pendulum would dominate. However, since this pendulum has a damping rate of 120 lbf - sec, this yields a value of
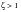
, indicating that an overdamped situation should exist so that a non oscillatory mode with essentially zero frequency should result.
Similarly, the second pendulum has a damping rate of 60 lbf - sec which is approximately equal to the average overall damping. Thus,
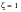
when the second oscillator dominates. When the
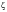
is equal to one, a critically damped situation exists which is once again characterized by non-oscillatory motion. Thus, there should be a second damped mode characterized by a natural frequency essentially equal to zero.
In the case of the second undamped mode, the motion is confined principally to the first and third pendulums. The lack of motion at the center pendulum effectively isolates the more lightly damped pendulum, thereby permitting an oscillatory motion to occur. Estimating the critical damping on the basis of the second undamped natural frequency gives:
and
This gives an estimated damped frequency for the second mode that is equal to:
Similarly, for the third undamped mode, the critical damping is
and
This gives an estimated damped frequency of
MSC Nastran Results:
To compute the complex modes for the coupled pendulums, the model shown in
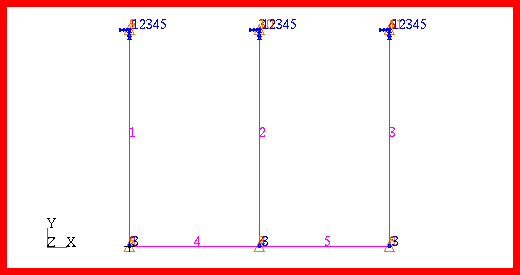
Figure 14‑53 was generated using Patran. The pendulums were modeled with a single massless CBAR element while the end masses were modeled using lumped CONM2 concentrated mass elements. The springs were modeled with CELAS1 linear springs while grounded CDAMP1 elements were used for the rotational dampers.
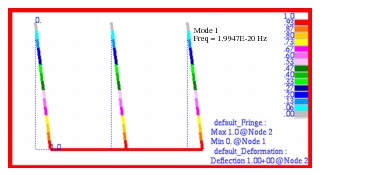
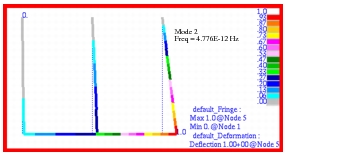
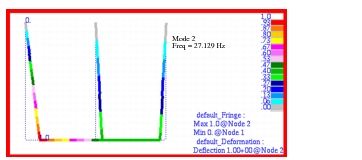
Using this model, the complex modes were recovered. The following natural frequencies were predicted for each complex mode:
Table 14‑19 Mode | Frequency (Hertz) |
1 | 1.994 x 10 -20 |
2 | 4.776 x 10 -12 |
3 | 27.129 |
4 | 55.802 |
The corresponding mode shapes were plotted using Patran and are shown in
Figure 14‑54 through
Figure 14‑57. Because of the presence of nonuniform damping, animation of any one of these modes will show a distinct phase difference in the motion of the individual pendulums.
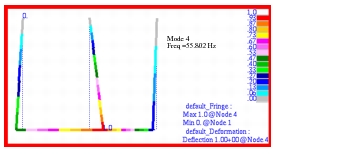
The complex modal frequencies agree quite closely with the estimated values. As expected, the first two modes involve motion of all three pendulums. The higher damping associated with two of the pendulums produces an overdamped condition which results in a modal frequency of essentially zero. The third mode primarily involves motion of the outermost pendulums, which corresponds to the second undamped mode shape. The predicted value of 27.129 hertz for this mode agrees very closely with the estimated value of 28.626 hertz. Similarly, the fourth mode is characterized primarily by motion at the center pendulum which corresponds to the third undamped mode. The predicted modal frequency of 55.802 hertz once again agrees very favorably with the estimated value of 57.896 hertz.
File(s): <install_dir>/results_vv_files/prob026.bdf, prob026.op2
Figure 14‑53 Model of Coupled Pendulums.
Figure 14‑54 Complex Mode 1 of Pendulums, Freq = 1.9994E-20 Hz.
Figure 14‑55 Complex Mode 2 of Pendulums, Freq = 4.776E-12 Hz.
Figure 14‑56 Complex Mode 3 of Pendulums, Freq = 27.129 Hz.
Figure 14‑57 Complex Mode 4 of Pendulums, Freq = 55.802 Hz.
Problem 27: Steady State Heat Transfer, Multiple Cavity Enclosure Radiation
Solution/Element Type:
MSC Nastran, Steady State Thermal Analysis, Solution 153, CQUAD4, CHBDYG, and RADCAV Elements
Reference:
MSC Nastran Thermal Analysis User’s Guide, Vol. 68, pp. 154-158.
Problem Description:
Four parallel plates radiate to each other and to the external ambient environment, assumed to be a perfect blackbody at a temperature of zero degrees K. If one of the plates is held at a constant temperature of
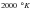
, find the temperature of the other three plates.
Engineering Data:
Theoretical Solution:
For the four parallel plates, the theoretical value of the view factor, F, between successive plates is F = 0.2
Thus,
Solving for
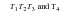
gives:
MSC Nastran Results:
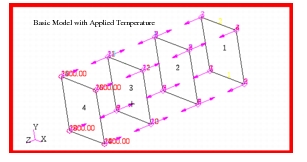
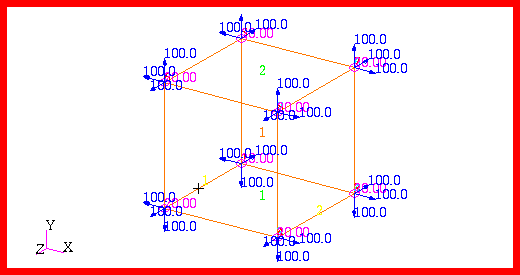
To solve for the temperatures of the plates, the model shown in
Figure 14‑58 was generated using Patran. The model consisted of 4 CQUAD4 elements. The radiation heat transfer was modeled using three separate radiation cavities that ignored the effects of any shading caused by the intermediate plates. In addition, no ambient element was specified which in effect simulated the effect of having a perfect black body at zero degrees kelvin to model the far field ambient conditions.
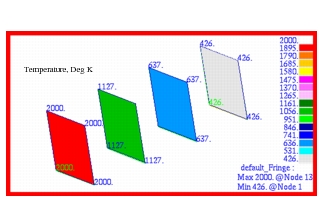
The resultant steady state temperatures that were calculated for each of the plates are shown plotted in
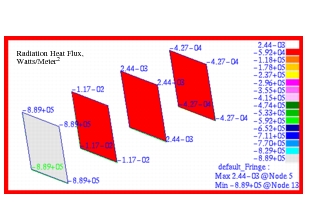
Figure 14‑59. The corresponding radiation heat fluxes are plotted in
Figure 14‑60 along with the actual nodal values for the radiation heat flux. Closer examination of the nodal fluxes reveals the tremendous decrease that occurs in the heat flux when multiple parallel plates are present.
Table 14‑20 Source | | | |
Theory | 1127.57 | 637.28 | 426.18 |
MSC Nastran | 1127.46 | 637.17 | 426.06 |
%, Difference | 0.01% | 0.02% | 0.03% |
File(s): <install_dir>/results_vv_files/prob027.bdf, prob027.op2
Figure 14‑58 Model of Four Parallel Plates.
Figure 14‑59 Steady State Temperatures of the Four Parallel Plates.
Figure 14‑60 Radiation Heat Fluxes of the Four Parallel Plate.
Problem 28: Transient Heat Transfer with Phase Change
Solution/Element Type:
MSC Nastran, Transient Thermal Analysis, Solution 159, CHEX8, CHBDYG, and CONV Elements.
Reference:
MSC.Nastran Thermal Analysis User’s Guide, Vol. 68, pp. 188-191.
Problem Description:
A cube of water is exposed to an ambient environment that is below the freezing point of water. In addition, the water is at an uniform initial temperature that is above the freezing point. Forced convection occurs along the lateral faces of the cube. Determine the time it takes for freezing to first occur as well as the total time required for all of the water to freeze.
Engineering Data:
Theoretical Solution:
If no phase change occurs, the heat balance equation is:
Assuming constant properties, then
The elapsed time required for complete freezing to occur is calculated from the following expression:
For this specific problem:
Substituting these values into the preceding equations gives:
MSC Nastran Results:
To model the freezing of the unit cube of water, the model shown in
Figure 14‑61 was generated using Patran. The cube was meshed with a single CHEX8 element. A uniform convective boundary condition was imposed along all of the exposed faces of the cube along with an initial temperature of -20
o C. The properties of water were assigned to the solid element and it was assumed that freezing would initiate at 0
o C and occur over a temperature range of 2
oC. A transient analysis was then performed with MSC Nastran using a fixed time step 5 seconds for a total duration of 5000 seconds.
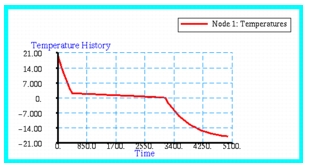
Using Patran, the temperature history was plotted for a single node situated at the base of the cube. The results are shown in
Figure 14‑62. Examining this figure, it is quite evident when the water began to freeze since the temperature will level off due to the release of the latent heat associated with the formation of ice. Once freezing has completed, the temperature will continue to decline until it reaches the ambient temperature, or
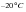
.
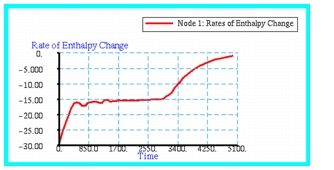
The corresponding rate of change in enthalpy is shown in plotted in
Figure 14‑63. Since the total enthalpy is just the product of the specific heat and temperature, during a phase change the rate of change of enthalpy should remain fairly constant. Afterward, the enthalpy will continue to decline at a decreasing rate as the ice asymptotically approaches the ambient temperature. This behavior is clearly evident in
Figure 14‑63.
Table 14‑21 Source | | |
Theory | 420 | 2718 |
MSC Nastran | 430 | 3100 |
%, Difference | 2.38% | 14.05% |
File(s): <install_dir>/results_vv_files/prob028.bdf, prob028.op2
Figure 14‑61 Model of Freezing Cube.
Figure 14‑62 Temperature Response of Freezing Cube.
Figure 14‑63 Rate of Enthalpy Change of Freezing Cube.
Problem 29: Steady State Heat Transfer, 1D Conduction and Convection
Solution/Element Type:
MSC Nastran, Steady State Thermal Analysis, Solution 153, CROD, CHBDYP, and CONV Elements.
Reference:
Chapman, A.J., Heat Transfer, 3rd ed., New York, MacMillan Publishing Co., Inc., 1974, p. 76.
Problem Description:
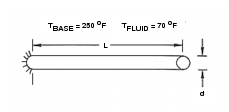
A fin of circular cross section is maintained at 250 o F at one end. The fin extends into air at an ambient temperature of 70 o F. Assuming a material conductivity of 132 Btu /hr-ft-oF and a surface convective film coefficient of 1.6 Btu / hr-ft 2-o F, determine the steady state temperature distribution along the length of the rod.
Engineering Data:
L = 1 ft d = diameter = 0.04167 ft A = lateral area = 0.001365 ft 2 k = thermal conductivity = 132 Btu / hr-ft-o F h = convective film coefficient = 1.6 Btu / hr-ft 2 -o F Tbase = 250 o F Tfluid = 70 o F | |
|
|
|
|
|
|
Theoretical Solution:
Assuming only 1D heat transfer along the length of the fin as well as no convective heat loss at the tip, the theoretical temperature distribution is
where
Substituting for m, gives the following steady state temperatures at four positions along the fin.
X / L | T (o F) |
.25 | 217.0243 |
.50 | 196.0559 |
.75 | 183.7156 |
1.00 | 179.7002 |
MSC Nastran Results:
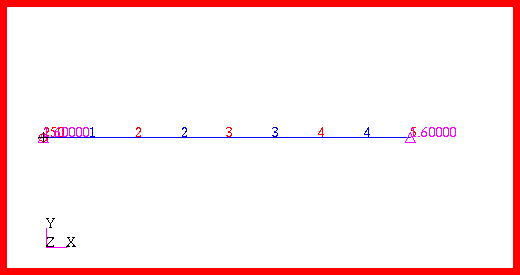
To compute the temperature distribution for the cooling fin, the model shown in
Figure 14‑64 was generated using Patran. The fin was modeled using 4 CROD elements. By doing so, this enabled the convective boundary condition to be modeled with line type CHBDYP convective boundary elements which alleviated the need to compute the lateral surface area associated with each node. Instead, this was determined by MSC Nastran from the cross-sectional area that was given for the rod.
Using the model shown in
Figure 14‑64, the nodal temperatures were computed. A fringe plot of the steady state temperature distribution that was generated by Patran is shown in
Figure 14‑65. Here the fringe labels have been included to better show the actual nodal values.
Table 14‑22 Source | X / L |
.25 | .50 | .75 | 1.00 |
Theory | 217.0243 | 196.0559 | 183.7156 | 179.7002 |
MSC Nastran | 217.7879 | 196.3183 | 184.0306 | 180.0316 |
%, Difference | 0.035% | 0.013% | 0.172% | 0.184% |
File(s): <install_dir>/results_vv_files/prob029.bdf, prob029.op2
Figure 14‑64 Model of Cooling Fin.
Figure 14‑65 Nodal Temperatures of Cooling Fin.
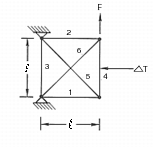
Problem 30: Freebody Loads, Pinned Truss Analysis
Solution/Element Type:
MSC Nastran, Linear Statics, Solution 101, CROD Elements.
Reference:
Przemieniecki, J.S., Theory of Matrix Structural Analysis, McGraw-Hill, Inc., 1968, p. 155.
Problem Description:
A pinned joint truss is loaded with a force at one end and one of the components is heated uniformly to an elevated temperature. Considering thermal effects, determine the freebody loads for each of the members in the truss.
Engineering Data:
This is a repeat of
Problem 8: Linear Statics, Pinned Truss Analysis, 55 except that the freebody forces will be plotted.
Theoretical Solution:
MSC Nastran Results:
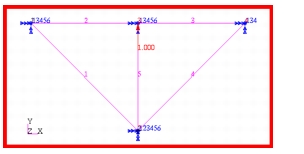
Using the model shown in
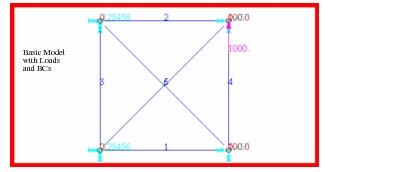
Figure 14‑66, the same results were obtained with MSC Nastran as in
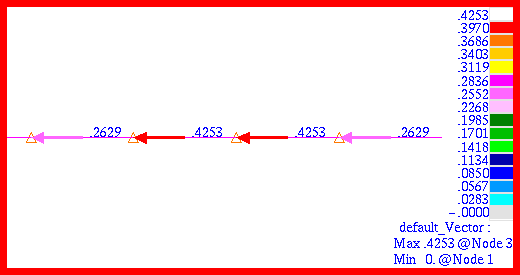
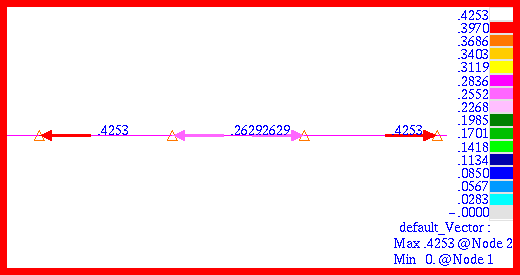
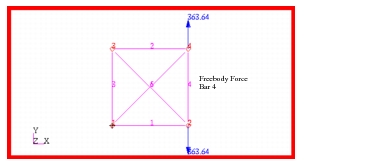
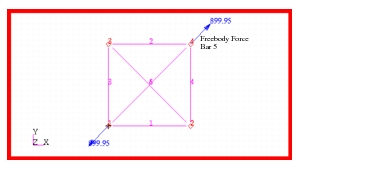
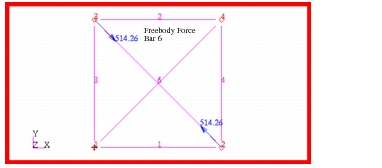
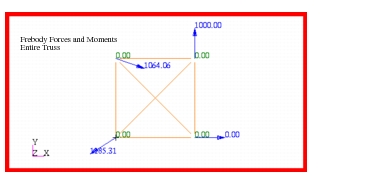
Problem 8: Linear Statics, Pinned Truss Analysis, 55. The Patran Freebody application was used to determine freebody force associated with every member of the truss. The resultant freebody forces computed by Patran are shown in
Figure 14‑67 through
Figure 14‑72. The freebody forces should be identical to the predicted rod forces which they are. The freebody forces and moments for the entire truss are plotted in
Figure 14‑73. The freebody moments are labeled in blue and are all zero in order to maintain rotational equilibrium. The results can be compared with
Table 14‑28.
File(s): <install_dir>/results_vv_files/prob030.bdf, prob030.op2
Figure 14‑66 Model of Pinned Truss.
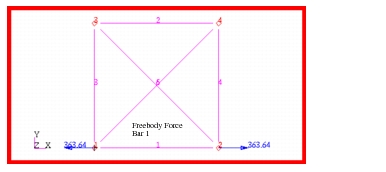
Figure 14‑67 Freebody Forces in Bar 1.
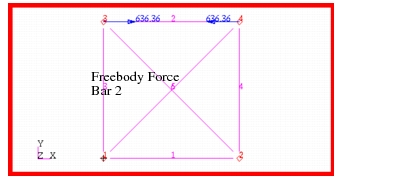
Figure 14‑68 Freebody Forces in Bar 2.
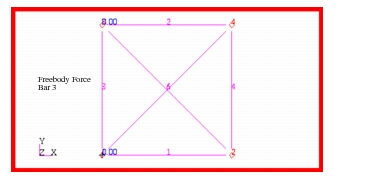
Figure 14‑69 Freebody Forces in Bar 3.
Figure 14‑70 Freebody Forces in Bar 4.
Figure 14‑71 Freebody Forces in Bar 5.
Figure 14‑72 Freebody Forces in Bar 6.
Figure 14‑73 Freebody Forces and Moments for Entire Truss.